平抛运动两种分解方法（平抛运动的另类分解法）

平抛运动一般处理方法是沿水平方向和竖直方向分解，水平方向做匀速直线运动，竖直方向做自由落体运动。

正交分解的坐标系建立是任意的，在不同的坐标系上描述的运动可能会不同。

例题：从倾角为θ的斜面上的A点，以初速度v₀，沿水平方向抛出一个小球，落在斜面上B点。从抛出开始经多长时间小球离斜面的距离最大？最大距离是多少？

当小球速度与斜面平行时，小球离斜面最远，因为速度与斜面平行，意味着速度在垂直斜面上没有分量，此时离斜面最远。

【常规解答】

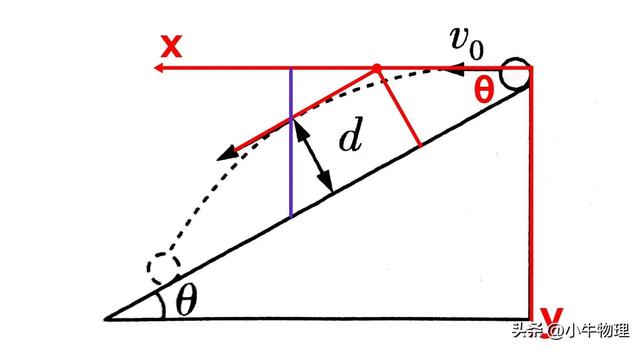
将平抛运动分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动。

速度与斜面平行时，小球离斜面最远。

d=(x/2)×sinθ

x=v₀t

v₀tanθ=gt⇒t=v₀tanθ/g

x=v₀t=v₀²tanθ/g

d=v₀²tanθsinθ/2g

【另类解答】

沿斜面和垂直斜面建立直角坐标系，如图所示：

运动的描述：

x轴：做初速度为v₀cosθ，加速度为gsinθ的匀加速直线运动；

y轴：做初速度为v₀sinθ，加速度为gcosθ的类竖直上抛运动。

离x轴最远，y轴上分速度为零，最远距离为：

(v₀sinθ)²/2gcosθ=v₀²tanθsinθ/2g。

比较简单易懂地解答了这道题。

也可以结合数学抛物线知识求解。