如何理解集合运算关系（谈谈集合运算）

话题：#科学# #数学# #集合论# #抽象代数# #测度论#

小石头/编

集合可能是唯一没有精确定义的数学概念吧，虽然 它构成数学的基础！（反正，小石头从中学到现在，也没有看到一个精确的集合定义，如果大家有，请发表在评论中。）

提到 集合 大体可以认为是一些对象 杂乱无章（也就是 无序）的放在一起，这些对象称为集合的 元素。概念来自哲学，其性质被称为 内涵，其涵盖的具体实例 的全体 被称为 外延，例如：

人，内涵 = 高级动物，外延 = 张三、李四、...

集合 也是一种概念，故 可以用 内涵 和 外延 两种方式定义，

• 内涵法：指定 集合元素 所满足的属性，基本形式是，
• E = {x | P(x) }
• 例如：令 P(x) = x是高级动物，则 人 = {x | P(x)}；

• 外延法：将 集合元素 罗列出来，基本形式是，
• E = {a, b, c, ⋯}
• 注：虽然罗列元素时，我们给元素排了一个顺序，但集合中元素是没有顺序的。
• 例如：人 = {张三,李四, ... }；

注：习惯上用，小写字母表示 非集合，用 大写字母表示 集合。

根据集合的定义，集合自身，自然附带一个元素与集合的关系判断：

如果 对象 x 是集合 E 的元素，我们 称 x 属于 E，记为 x ∈ E，反之 则 x 不属于 E，记为 x ∉ E := ¬(x ∈ E)。

※※※

为了描述清楚，本文会使用 一阶逻辑语言，它由以下三部分组成：

• 逻辑值：真 1，假 0；
• 逻辑运算：
• 一元 ：非 ¬；
• 二元： 与 ∧，或 ∨，蕴含 ⇒，等价 ⇔；
• 任意元（包括 零元）：恒真 ⊤ ，恒假 ⊥；
• 量词：全称量词 ∀ ，存在量词 ∃；
• 用 := 表示定义。

一阶逻辑语言和自然语言之间翻译对照为：

• 1 = 真，0 = 假；
• ¬ x = 不是 x，非 x；
• x ∧ y = x 且 y；
• x ∨ y = x 或 y；
• x ⇒ y = 如果 x 那么 y，若 x 则 y；
• x ⇔ y = x 当且仅当 y，x 的从要条件是 y；
• ⊤ = ⊤(x, ...) = 真，⊥ = ⊥(x, ...) = 假；

• ∀ x ∈ E, y = 对于E中的任意 x 都有 y；
• ∃ x ∈ E, y = E中存在 x 使得y；
• ∃! x ∈ E, y = E中存在唯一 x 使得y；
• x := y = x 定义为 y。

关于 一阶逻辑语言 更详细的内容，可参考 小石头 首页 的文章《 一阶逻辑简介》或 相关的逻辑学书籍。

※※※

有了 ∈（∉） 后，我们就可以其为基础，就定义 集合关系 和 集合运算 了：

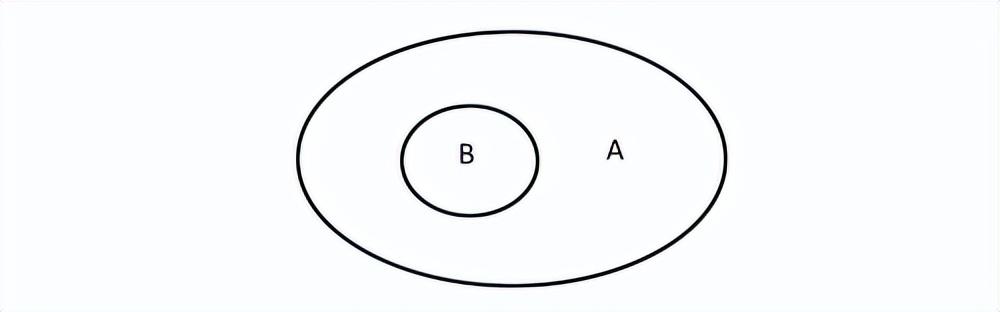
如果 集合 B 的 所有 元素 都属于 集合 A，则称 B 包含于 A 或 A 包含 B，记为，

• B ⊆ A 或 A ⊇ B := ∀ x∈B ⇒ x∈A

同时，我们也 称 B 是 A 的子集， A 是 B 的 超集。集合 A 的所有子集，组成的集合称为 A 的 幂集，记为，

• P(A) := {B | B ⊆ A } ❹

像幂集这种，元素是集合的 集合，称为 集族（或 集系 、集类）。

注：习惯上用，大写花体或粗体来表示 集族。

集合还是比较抽象的，不过我们可以借助 Venn图 来辅助理解（记得小石头小时候全靠它了），这里的包含可绘制如下图：

若 A 和 B 相互包含，则 A 和 B 相等，即，

• A = B := A ⊆ B ∧ B ⊇ A ❶

交 和 并 可能是大家接触最早的 两种集合运算吧！（小石头是高一初见的，不知道大家是啥时候？）

两个集合 A 与 B 的 交 运算定义为：

• A ∩ B := { x | x∈A ∧ x ∈ B }

其结果，是 两集合共同拥有的元素组成的集合，称为 交集。交 的 Venn图如下：

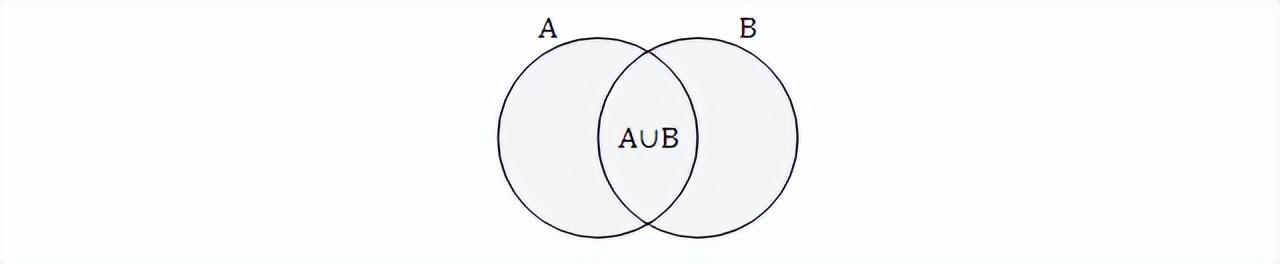
两个集合 A 与 B 的 并 运算定义为：

• A ∪ B := { x | x∈A ∨ x ∈ B }

其结果，是 两个集合的元素和在一起组成的集合，称为 并集。并 的 Venn图如下：

又设 E 是集族，我们 还可 分别 升级 交 与 并 运算为：

• ∩ E := {x | ∀ A ∈ E， x ∈ A }
• ∪ E := {x | ∃ A ∈ E， x ∈ A } ❸

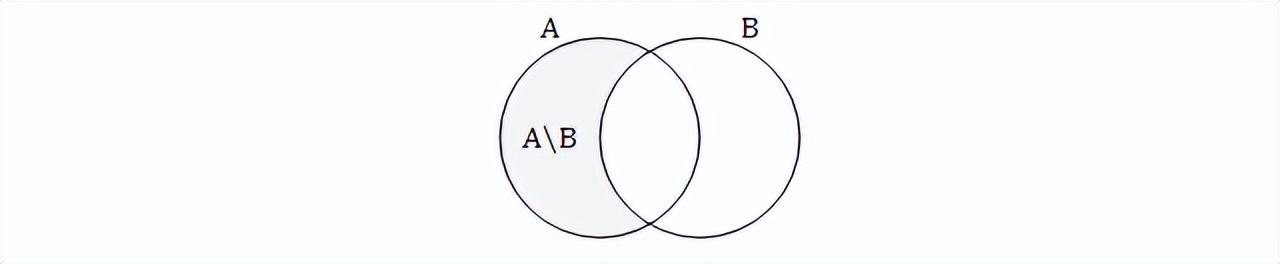
并集，其实就是将 B 中的元素添加到了 A 中的结果，与之相反，从 A 中除去B中的元素 则 得到 差集，对应 的差 运算定义为：

• A \ B = { x | x∈A ∧ x ∉ B}

差 并不要求 A 一定包含 B，其 Venn图如下：

---

专门研究集合的数学叫集合论，集合论中要求集合必须满足：

• 一个对象是否属于一个集合 必须是明确的； ☆

可是实际上，前面集合的内涵定义，有时候并不满足这个要求，例如：

用内涵法定义集合

• E = {x | x ∉ E}

判断 E 是否属于它自己？

• 如果 E ∈ E，则 它 就不符合 属性 x ∉ E，于是 E ∉ E，矛盾！
• 如果 E ∉ E，则 它就 符合 属性 x ∉ E，于是 E ∈ E，矛盾！

无论怎样都会产下矛盾，也就是说，E 不满足 ☆，这就是 著名的 罗素悖论，其通俗版本就是，

• 理发师悖论：村里的理发师宣称：“我不给，给自己刮胡子的人，刮胡子”，于是有人问：“那你给自己刮胡子吗？”。

罗素悖论直接导致了第三次数学危机，为了应对危机，数学家想了一个方法 ①：

• 先指定一个满足☆的集合 X，然后在 X 范围内 使用 内涵法，基本形式是，
• E = {x∈ X | P(x) } ❷
• 这样以来，定义结果 一定是 X 的子集，自然也就满足☆了。

一般来说，X 包含了 上下文 所需要研究 的所有对象，是最大的集合，被称为 全集。

※※※

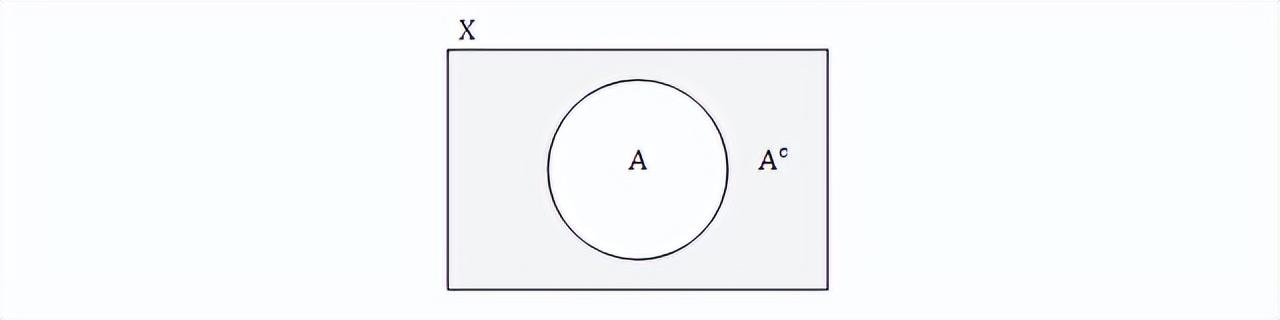
有了全集 X 后，我们就可以定义 补运算了：

• Aᶜ = X \ A

其中 Aᶜ 称为 A 的补集。 补 的Venn图如下：

与全集相对是 空集，它不包含任何元素，可定义为：

• 内涵法：∅ := {x| x≠x}；
• 外延法：∅ := { }；

这两种定义等价。

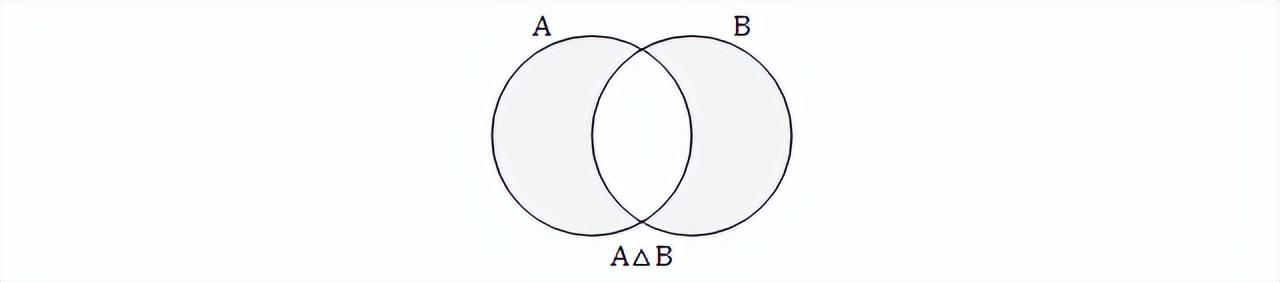
最后，还有一种不常见的 对等差 运算，定义为：

• A △ B = (A\B) ∪ (B\A)

它用来 表示两个 集合 A 和 B 差异 ，其 Venn图如下：

显然有，

• A △ B = ∅ ⇔ A = B

---

方法 ① 仅仅是 数学家 的权宜之计，并不能从根本上解决问题，这对于 逻辑学家 是不能容忍的，于是他们另想了一个主意：

• 内涵法 不一定满足☆ 是事实，这意味着，内涵法的定义结果不一定是集合，于是 干脆 将其改称为 类；
• 类 可以 是集合（满足☆） ，也可以 不是（不不满足☆）这时称为 真类；
• 从公理化思维角度看，内涵法 和 外延法 分别 是 集合 的唯二 的 两大 公理，现在：
• ○ 外延法 没问题，保留！称为 ◎ 外延公理 ：就是 前面的 ❶；
• ○ 内涵法 有问题，于是 考虑 找寻 一组 公理 来替代它！逻辑学家总共找到8个：
• ◎ 配对公理： 任意 a, b 都可组成 集合 {a，b}，称为 无序对；
• ◎ 分离公理图式：就是前面的 ❷；
• ◎ 并公理：就是前面的 ❸；
• ◎ 幂集公理：就是前面的 ❹；
• ◎ 无限公理：存在一个无限集；
• ◎ 替换公理图式：若 F 是定义在 A 上的 函数，则存在 集合 F(A) := {F(x) | x ∈ A}；
• ◎ 正则公理：集合不能直接或间接的属于自己（防止罗素悖论）；
• ◎ 选择公理： 任何 非空集合组成的集族 上，都存在 选择函数，它自每一个元素集合中选择一个元素组成新的集合。

以上这 九个公理，这就是大名鼎鼎的 ZFC 公理。

至此， 第三次数学危机，基本上已经被解决了，但还留了一个尾巴：

• 在完备性上，再多的公理 也 不可能 完全 替代内涵法（详见 哥德尔不完备定理）

不过也只能这样了。

---

其实我们最熟悉的运算是算术四则运算：加减乘除，其中减和除分别是加和乘的逆运算。在有理数域ℚ内考察，加（ ）和乘（⋅）运算，我们发现它们具有如下性质：

运算	结合律	单位	可逆	交换律	分配律
	(a b) c=a (b c)	0 a=a	a (-a)=0	a b=b a
⋅	(a⋅b)⋅c=a⋅(b⋅c)			a⋅b=b⋅a	a⋅(b c)=a⋅b a⋅c

称具有这样性质的 (ℚ, , ⋅) 为 环；与之比较，集合运算的对等差和交具有如下性质（设，X 是非空集合，在P(X)中考察）：

运算	结合律	单位	可逆	交换律	分配律
△	(A△B)△C=A△(B△C)	∅△A=A	A△Aᶜ=∅	A△B=B△A
∩	(A∩B)∩C=A∩(B∩C)			A∩B=B∩A	A∩(B△C)=(A∩B)△(A∩C)

故，(P(X), △, ∩) 也构成一个 环。 再进一步，若 非空集族 E 满足：

• 对 并封闭，即，A∈E, B ∈E ⇒ A∪B∈E；
• 对 差封闭，即，A∈E, B ∈E ⇒ A\B∈E；

则有，

∅ = A \ A ∈ E

而，

A △ B = (A \ B) ∪ (B \ A) ∈E

A∩B =(A∪B) \ (A△B) ∈E

故， E 具有表二要求的运算，于是 E 是 环。

※※※

逻辑运算：或（∨）、与（∧）、非（¬），是我们接触的另外一类运算，发现它们具有如下性质（在 布尔值集 B={0, 1} 中考察）：

运算	交换律	结合律	吸收律	分配律	单位
∨	a∨b=b∨a	(A∨B)∨C=A∨(B∨C)	a∨(a∧b)=a	A∨(B∧C)=(A∨B)∨(A∨C)	0∨a=a	a∧¬a=1
∧	a∧b=b∧a	(A∧B)∧C=A∧(B∧C)	a∧(a∨b)=a	A∧(B∨C)=(A∧B)∨(A∧C)	1∧a=a	a∧¬a=0

称具有这样性质的 (B, ∨, ∧, ¬) 为 布尔代数；将集合运算：交、并、补，与之比较有（依旧在 P(X)中考察）：

运算	交换律	结合律	吸收律	分配律	单位
∪	A∪B=B∪A	(A∪B)∪C=A∪(B∪C)	A∪(A∩B)=A	A∪(B∩C)=(A∪B)∩(A∪C)	∅∪A=A	A∪Aᶜ=X
∩	A∩B=B∩A	(A∩B)∩C=A∩(B∩C)	A∩(A∪B)=A	A∩(B∪C)=(A∩B)∪(A∩C)	X∩A=A	A∩Aᶜ=∅

我们发现，(P(X), ∪, ∩, ᶜ) 构成一个 布尔代数。更进一步，对于任意非空集族 E ，如果满足：

• 对 并封闭；⑴
• 对 补封闭，即，A∈E ⇒ Aᶜ∈E；

则有，

X = A∪Aᶜ ∈ E

∅ = Xᶜ ∈ E

又根据德摩根定律有，

A∩B = ((A∩B)ᶜ)ᶜ = (Aᶜ∪Bᶜ)ᶜ ∈E

于是，E 就能满足表四的性质了，故 E 是 （布尔）代数。

注：另外，从表四中，我们还能看出，(P(X), ∪, ∩) 距离 成环，只少一个 可逆 的性质，于是称 其为 半环。环E，要求 对 并 和 差 封闭，而 半环 要求，对 交封闭，并且 对于任意A, B ∈ E，B ⊆ A ，都存在 两两不相交 的 C₁, C₂, ..., Cᵣ ∈ E 使得，A\B = C₁∪C₂∪⋯∪Cᵣ 。

※※※

对于 任意 代数 E，因，

A \ B = A ∩ Bᶜ

故 E 是满足 X∈ E 的 环，称为 布尔环； 反过来 对于 布尔环 E，则有，

Aᶜ = X \ A；

故 E 是 代数。

※※※

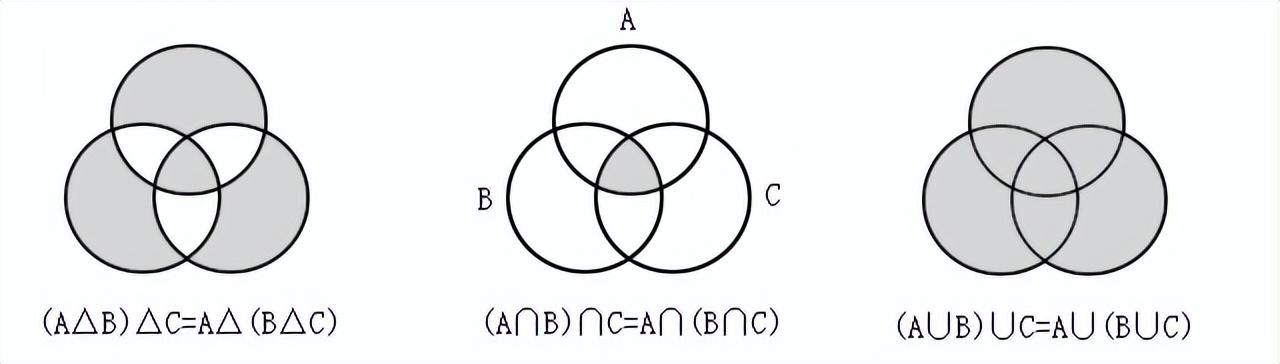
以上的集合运算性质的详细证明省略（留给大家完成），这里仅通过Venn图简单的佐证一部分，

结合律：

分配律：

---

《高等数学》中极限，大家都听说过，其实用集合的运算，同样可以定极限：对于 集合序列 A₁, A₂, A₃, ...，

• 若 A₁ ⊆ A₂ ⊆ A₃ ⊆ ...，则称为单调递增的，并 定义极限：
• ○ limn→∞ An = ∪ᵢ₌₁∞ Aᵢ = A₁∪A₂∪A₃∪⋯；
• 若 A₁ ⊇ A₂ ⊇ A₃ ⊇ ...，则称为单调递减的，并 定义极限：
• ○ limn→∞ An = ∩ᵢ₌₁∞ Aᵢ = A₁∩A₂∩A₃∩⋯；

对于任何序列 A₁, A₂, ...，我们总能构造，

• 单调递增序列： B₁ = A₁∩A₂∩A₃∩⋯ ⊆ B₂ = A₂∩A₃∩⋯ ⊆ B₂ = A₃∩⋯ ⊆ ⋯，于是定义下极限：
• ○ lim inf n→∞ An = limn→∞ Bn；
• 单调递减序列：B₁ = A₁∩A₂∩A₃∩⋯ ⊇ B₂ = A₂∩A₃∩⋯ ⊇ B₃ = A₃∩⋯ ⊇⋯，于是定义上极限：
• ○ lim sup n→∞ An = limn→∞ Bn；

当上下极限相等时，则称 序列 的 极限存在，并记为：

• limn→∞ An = lim inf n→∞ An = lim sup n→∞ An

※※※

考虑，代数 E，若将其条件⑴ 从对 并封闭，改为：

• 对 可列并封闭（也成 E 具有 σ 性），即，A₁, A₂, A₃, ... ∈ E ⇒ A₁∪A₂∪A₃∪⋯∈E；

则有，

A₁∩A₂∩A₃∩⋯ = (( A₁∩A₂∩A₃∩⋯)ᶜ)ᶜ = (A₁∪A₂∪A₃∪⋯)ᶜ ∈E；

于是，E 就支持了 上面 的 极限定义，此时称 E 为 σ 代数。类似地，具有 σ 性的环 σ 环，称为 σ 环（或 σ 代数） 是 可测空间 的基础。

---

（好了，乱七八糟地，就和大家聊这么多了。集合是从高中阶段开始接触的，比较抽象的概念之一，它对于数学至关重要，希望这篇文章对大家理解集合有所帮助。最后，小石头 在这里 祝大家 五一节 玩的高兴！）

,