数学化简求值题综合讲解（利用绝对值的几何意义巧解距离和最值问题）

哈喽，大家好！我们又见面了，欢迎继续关注【轩爸辅导】的【口袋数学】。日更【每日一学】【每日一练】，帮助孩子日积月累，考出好的成绩。配套辅导，哪里不会学哪里，哪里出错练哪里，帮助孩子提高效率。

从数轴上看|a|表示数a的点到原点的距离；|a-b|表示数a、数b的两点之间的距离。

|a-b| 的几何意义就是数轴上数a、数b的两点之间的距离。

|x-a1| |x-a2| 就表示数x的点到数a1、a2两点的距离和，当a1≤x≤a2时，距离和最小且为a1、a2两点之间的距离|a1-a2|。

|x-a1| |x-a2| |x-a3| 就表示数x的点到数a1、a2、a3三点的距离和，当x=a2时，距离和最小且为a1、a3两点之间的距离|a1-a3|。

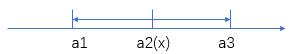
以此类推，求数x在到偶数个点的距离和，x在最中间两个点之间时，距离和最小；求数x在到奇数个点的距离和，x与最中间一个点重合时，距离和最小。

01 典型例题讲解

例1. 点A、B在数轴上分别表示有理数a、b，点A与原点O两点之间的距离表示为AO，则AO＝|a-0|＝|a|，类似地，点B与原点O两点之间的距离表示为BO，则BO＝|b|，点A与点B两点之间的距离表示为AB＝|a-b|.

请结合数轴，思考并回答以下问题：

（1）①数轴上表示1和－3的两点之间的距离是________；

②数轴上表示m和－1的两点之间的距离是________；

③数轴上表示m和－1的两点之间的距离是3，则有理数m是________；

（2）若x表示一个有理数，并且x比－3大，x比1小，则|x-1| |x 3|=________

（3）求满足|x-2| |x 4|=6的所有整数x的和________.

【分析】

（1）根据数轴上的点确定两点之间的距离，根据绝对值的性质得出结果并总结规律；

（2）在（1）中规律的基础上得出符合条件的值；

（3）结合数轴和点在数轴上的特征得出符合条件的x的值，计算和即可.

【解答】

解：⑴①数轴上表示1和－3的两点之间的距离是|1-（-3）|=4；

②数轴上表示m和－1的两点之间的距离是|m-（-1）|=|m 1|；

③根据题意，得|m-（-1）|=3，即|m 1|=3，解得m=2或-4；

⑵由x比－3大，x比1小，则|x-1| |x 3|表示在1和-3之间的一点，到1的距离与到-3的距离的和，即等于1到-3的距离4；

⑶把问题转换为求x到点2和点-4的距离之和等于6的点，则x大于等于-4，且小于等于2，故x可以取-4，-3，-2，-1，0，1，2，共7个。

这7个数的和为（-4） （-3） （-2） （-1） 0 1 2=-7.

02 举一反三练习

1. 数轴上从左到右的三个点 A ，B ，C 所对应的数分别为 a ，b ，c ．其中AB=2017，BC=1000，如图所示．

（1）若以B为原点，写出点A，C所对应的数，并计算a＋b＋c 的值．

（2）若原点 O 在 A，B 两点之间，求 |a| |b| |b-c| 的值．

（3）若O是原点，且OB=17，求a b－c的值．

2. 同学们，我们都知道：|5-2|表示5与2的差的绝对值，实际上也可理解为5与2两数在数轴上所对应的两点之间的距离；|5 2|表示5与-2的差的绝对值，实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离，试探索：

（1）|﹣4 6|=________；|﹣2﹣4|=________；

（2）找出所有符合条件的整数x，使|x 2| |x-1|=3成立；

（3）若数轴上表示数a的点位于﹣4与6之间，求|a 4| |a﹣6|的值；

（4）当a=________时，|a﹣1| |a 5| |a﹣4|的值最小，最小值是________；

（5）当a=________时，|a﹣1| |a 2| |a﹣3| |a 4| |a﹣5| … |a 2n| |a﹣(2n 1)|的值最小，最小值是________.

03 参考答案解析

1. 【答案】

（1）解：以B为原点,点A,C对应的数分别-2017,1000

a b c=-2017 0 1000=-1017

（2）解：当原点O在A,B两点之间时, |a| |b| =2017,|b-c|=1000

|a| |b| |b-c|=2017 1000=3017

附另一解法：点A,B,C对应的数分别b-2017,b,b 1000

|a| |b| |b-c|=2017-b b 1003017

（3）解：若原点O在点B的左边,则点A,B,C所对应数分别是a=-2000，b=17，c=1017

则a b-c=-2000 17-1017=-3000

若原点O在点B的右边,则点A,B,C所对应数分别是a=-2034，b=-17，c=983

则a b-c=-2034 (-17)-983=-3034

2. 【答案】

（1）2；6

（2）解：此题可以理解为数轴上一点到-2,1的距离的和是3，由于1到-2 的距离就是3,，故当-2≤x≤1的时候即可满足条件，又因为x是整数，所以x的值可以为：-2，-1,0,1.

（3）解：∵数轴上表示数a的点位于﹣4与6之间，∴a 4＞0，a﹣6＜0，∴|a 4| |a﹣6|=a 4-a 6=10;

（4）1；9

（5）1；n(2n 3)

【分析】

（1）由于绝对值符号具有括号的作用，先按有理数的加减法法则算出绝对值符号里面的，再根据绝对值的意义去掉绝对值符号即可；|﹣4 6|=|2|=2，|﹣2﹣4|=|-6|=6；

（2）此题可以理解为数轴上一点到-2,1的距离的和是3，由于1到-2 的距离就是3,，从而找出1到-2 的整数即可；

（3）根据有理数的加减法法则，首先判断出a 4＞0，a﹣6＜0，再根据绝对值的意义去掉绝对值符号合并同类项即可；

（4）此题可以理解为数轴上一点到1，-5,4的距离的和最小，根据两点之间线段最短，故当a表示的数是介于4和-5之间的数1的时候，即可使其值最小，然后将a=1代入再根据绝对值的意义化简即可；

当a=1的时候，|a﹣1| |a 5| |a﹣4|=|1﹣1| |1 5| |1﹣4|=9；

（5）根据（4）的规律，此题可以理解为数轴上一点到1，-2,3，-4…-2n,(2n 1)的距离和最小，根据两点之间线段最短，故当a=1的时候，其值最小。当a=1的时候，

|a﹣1| |a 2| |a﹣3| |a 4| |a﹣5| … |a 2n| |a﹣(2n 1)|

=|1-1| |1 2| |1-3| |1 4| |1-5| … |1 2n| |1-(2n 1)|

=0 3 2 5 4 … |2n 1| |2n|

=2 3 4 5 … 2n (2n 1)

=n(2n 3)

转载请注明：轩爸辅导 » 【口袋数学】利用绝对值的几何意义巧解距离和最值问题 #提分#

,