五年级上册数学多边形的面积笔记（五年级上册数学多边形的面积-回顾整理）

《多边形的面积-回顾整理》学历案

【课题与课时】

青岛版小学数学五年级上册第五单元“多边形的面积"复习整理1课时

【课标要求】

《义务教育数学课程标准》（2021年版新课标）中关于多边形的面积有如下要求：

1. 内容要求：探索并掌握平行四边形、三角形和梯形的面积公式；
2. 学业要求：会计算平行四边形、三角形与梯形的面积，能用相应公式解决现实情境中 的问题。

【学习目标】

1. 通过课前整理“多边形面积"的知识树，整体回顾本单元知识。并网络图，构建知识 间的联系。初步形成知识网络，增强对知识的运用能力。
2. 通过小组合作学习，分组汇报，重现面积推导过程，复习多边形的面积公式，并通过 梳理知识结构图，理解长方形、平行四边形、三角形、梯形之间的联系。初步形成“转化” 的数学思想。
3. 通过计算四种平面图形的面积，明确“92”的意义。突破难点和易错点，让模糊的知 识清晰化。感悟“转化”的数学思想。
4. 经历用以盈补虚法推导三角形面积的过程，理解计算组合图形的多种算法，并能正确 灵活地运用公式进行计算，发展空间观念。

【评价任务】

1. 小组内说一说你是怎样对本单元知识进行整理的。互相指一指还有哪些地方需要完 善？你更喜欢谁的整理方法？为什么？（检测学习目标1）
2. 四个人商量下，推荐哪些方法和全班同学交流呢？那如果把多边形的面积公式看作一 棵知识树的话，你认为哪种图形具有“树根'‘的作用？理由呢？（检测学习目标2）
3. 数一数，算一算这四个图形的面积。注意每个小方格的边长都是1厘米，请你在图形 下面写算式，计算一下。（检测学习目标3）
4. 你能试着用这种转化的方法推导出三角形的面积公式吗？那梯形可不可以呢？（检测 学习目标4）

【资源与建议】

1. 本单元是在已经初步认识了长方形、正方形、三角形、平行四边形、梯形的特征及长 方形和正方形面积计算的基础上进行学习的，是今后学习立体图形知识的基础，平行四边形、 三角形、梯形的面积计算是几何与图形领域中的重要内容，在日常生活中有广泛的应用。
2. 本课的学习按以下流程进行：梳理，让零散的知识系统化一-补缺，让模糊的知识清晰 化一-提升，让已有的知识活化。

本课的重点是：整理完善知识结构、灵活解决实际问题。

本课的难点是：掌握多边形面积公式之间的联系。通过学生动手操作，用剪拼的方法把

一个三角形转化为一个长方形，找出两个图形之间的联系，推导出三角形的面积计算公式。

课前交流

师：同学们，很高兴有机会和咱们五X班的同学一起学习，一直听说咱班同学聪慧，那

作为龙泉中心的小主人，给大家介绍一下自己吧！谁先来（学生站起来后说：可以具体点），

生：大家好，我叫，喜欢跑步和打篮球，曾经参加过XX比赛获得一等奖

师：真不错，小运动健将。

生：我叫，是一名喜欢体育的男孩，曾经参加过XX比赛获得一等奖

师：你也很棒，据我所知咱班还有很多书法高手，是哪几位？给大家挥挥手。

咱班可真是藏龙卧虎啊，真是没想到。但是正是因为这份没想到，让我对这节课有了更

多的期待，下面咱们开始上课可以吗？

【学习过程】

一、梳理，让零散的知识系统化
学习目标1	学生活动1	教师指导1	学习评价1
通过课 前整理“多 边形面积" 的知识树， 整体把握 多边形的 面积的知 识点，初步 形成知识 网络，增强 对知识的 运用能力。 通过小	整体梳理 小组讨论： 小组内说一说自己是怎样对本单元 知识进行整理的。 互相指一指还有哪些地方需要完善？ 四个人商量一下，打算推荐哪些方法在 全班交流。	师：课前我们对本单 元知识进行了复习和 整理，请拿出你的作 品。1.组内交流。说 一说你是从哪些方面 整理的，整理了哪些 内容？互相指一指还 有哪些地方需要补充 完善。 2.组内商量下，你们	生生互评： 整理的完整、 讲解的有理 有据 教师评价 （1） 乐于交 流，敢于表达 （ 1） （2） 能说出 自己的想法， 表达严谨，有 理有据（ 1）

组合作学 习，分组汇 报，重现面

打算推荐哪些方法与 全班同学交流。

积推导过程，复习多

边形的面 积公式，并 通过梳理 知识结构 图，理解长 方形、平行 四边形、三 角形、梯形

之间的联

系。初步形

成“转化”

的数学思

想。

分模块整理汇报:

组1:重点复习平面图形面积的推导

过程。

生1:本单元我们学习了：平行四边

形、梯形、三角形的面积公式

生2：

生5：我们认为延高剪开是关键

构建网络

组2：用网络图的方式整理平面图形

之间的联系。

师：其他组还有 什么建议或者还有什 么要补充的吗？

我们认为：

我们认为由长方形的面积公式可以推 导出平行四边形的面积公式，根据平行

生评价1组： 很清楚，汇报 的也很有顺 序。

师评价1组： 分工明确，而 且用了表格 列举的方法， 直观形象，值 得提倡。

生评价2组： 我觉得这种 方法非常直 观，这种用图 表示它们之 间的关系的 方法是我没 想到的。

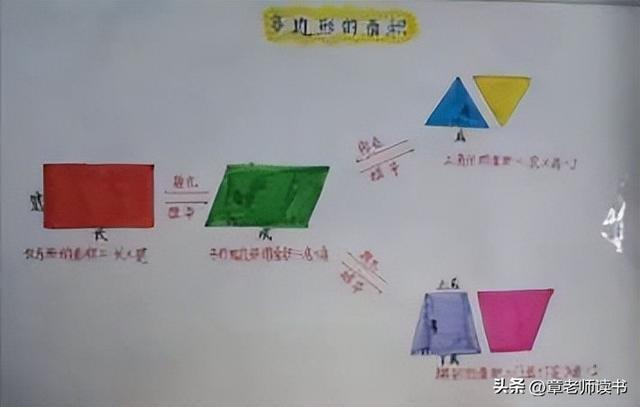
四边形的面积公式我们也可以推导出 三角形和梯形的面积公式，只需要用两 个完全一样的三角形和梯形都可以拼 成平行四边形。

师：之前我们还学过 正方形的面积，那大 家觉得可以在这个图 的哪个位置上表示出 来？谁来摆一摆。

师：如果把多边形的 面积公式看作一棵大 树的话，你认为哪种 图形具有“树根”的 作用？（绘制关系图）

师小结并渗透转化的 思想方法。

二、补缺，让模糊的知识清晰化

学习目标2 3.通过计 算四种平 面图形的 面积，明确

的 意义。突破 难点和易 错点，让模 糊的知识 清晰化。感 悟“转化” 的数学思 想。

学生活动2

1. 学生数一数，算一算这四个图形的面 积。
2. 明确梯形和三角形面积公式中92 的含义。

生1：如果不：2,算的就是两个这样 的梯形或三角形的面积了。

教师指导2

师：看下边这四个图形,

有什么想说的么？

质疑：梯形、三角形 的面积公式中都有：

2,为什么92后面积

还相等？不除以2算

的是谁的面积？

学习评价2

1.会交流，敢 表达，有理有 据( 1)

2.能正确计 算平面图形 的面积，计算 正确，表达严 谨( 1)

三、补缺，让已有的知识活化

学习目标3	学生活动3	教师指导3	学习评价3
4.经历用 以盈补虚 法推导三 角形面积 的过程，理 解计算组 合图形的 多种算法， 并能正确	1.生：它的顶点一格一格的向右平移， 形状变了，面积没变。	1.师：这个直角三角 形是如何变化的？变 化过程中，什么变了？ 什么没变？

灵活的运 用公式进 行计算，发 展空间观 念。

2.图中深色的三角形 形状相同么？面积 呢？

1. 比较两个三角形面积的大小。

3.直角三角形想通过 不同的变化，使面积 保持不变，你们能帮 帮直角三角三角形 吗？

1. 还可以变成底6格、高4格 还可以变成底8格、高3格 还可以变成底12格、高2格 .....

只要底与高的乘积不变，面积就不变。 解决易错题训练

1. 面积相等的两个三角形一定等底

等高吗？

4.引导学生从新的视 角理解面积。

1. 两个等底等高的三角形，它们的

形状一定相同吗？

1. 从新认识“面积”

1.理解以盈补

面积

• •

15

长度

虚，会用

“割”、“补”

的方法解题，计

算正确( 1)

2.思路严谨、表

达准确( 1)

5.生分组研究用一个三角形转化成长

方形，并尝试推导三角形的面积公式。

K方形的成枳 =K X 宽

II II II

为形的ihi砍=成X〈样寻2)

师：同学们可真 聪明，想到了古 代数学家想到 的方法。

5师：直角三角形是 怎样变化的？在变化 过程中，什么变了？ 什么没变？

师：你能根据这个转 化过程推导三角形的 面积公式吗？

师：你能利用这节课 学习的方法求出下面 图形的面积吗？

6.观看视频，理解以盈补虚。

学生用“割''“补"法求这两个图形的 面积。

板书设计多边形的面积■回顾整理

【学后反思】

1. 请你根据平面图形的面积的推导过程，梳理本单元的知识,点、重要数学思想和方法。
2. 学习后还存在什么问题或困惑？

设计说明：撰写“学后反思”需要一定的指导语，为了帮助学生理解，可以对“指导语”

进行适当的解释。

,