支持向量机的方法（支持向量机SVMSupportVector）

一、支持向量机（SVM: support vector machine）

support vector machine (SVM): a support vector machine is supervised machine learning model that uses classification algorithms for two-group classification problems. After giving an SVM model sets of labeled training data for each category, they’re able to categorize new text.

支持向量机是一种使用分类算法解决二分类问题的监督学习模型。

上图中不同颜色的点表示不同的类型（class)，找到一个平面使得两类support vector支持向量之间的距离(margin)最大。之间的距离通过计算后得

，分类问题就变成了一个求解

最大值的过程，即求解

的最小值的过程。具体理论计算网上找找会有很多写得很全面的文章。理论我就不多赘述啦。下面还是直接来代码比较实际一点。希望看完对大家有些帮助。

上面图片中用直线就可以将这些点划分两个区域了，但在实际很多情况下，只是 线性划分并不能将这两个不同颜色的类别划分开来。如下右图，这种无法用线性划分的，我们应该可以用一条封闭的曲线将两个类别划分开来。接下来本文会用代码针对线性和非线性的情况分别进行划分。

二、支持向量机处理线性关系问题：‍

关注公众号查看，体验更佳哦～

%matplotlib inline

import numpy as np

import matplotlib.pyplot as plt

from scipy import stats

# use Seaborn plotting defaults

import seaborn as sns; sns.set()

from sklearn.datasets.samples_generator import make_blobs

X, y = make_blobs(n_samples=[10,20,30], centers=[[0,0],[1,1],[2,2]], random_state=0, cluster_std=0.30)

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

X, y = make_blobs(n_samples=50, centers=2,random_state=0, cluster_std=0.60)

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

sklearn.datasets.samples_generator.Make_blobs

(n_sample=100,n_features=2,*,centers=None,cluster_std=1.0,random_state=None,renturn_centers=False,...)‍

Make_blobs: generate isotropic Gaussian blobs for clustering。生成各向同性的高斯斑点用来进行聚类。

N_samples: int,optional(default=2)

N_samples为数组时，则序列中的每个元素表示每个簇(cluster)的样本数。此时对应的center里面也需要写出每个簇(cluster)中心点的坐标。比如在N_sample=[10,20,30]的时候，表示有三个簇(cluster)，他们每个簇点的个数分别为10个，20个和30个，此时在对应的centers参数中就要设置这三个簇(cluster)的中心坐标，这里设置为centers=[[0,0],[1,1],[2,2]]，那么三个中心点（x,y）对应的坐标分别为（0，0），（1，1），（2，2），在上面的图中分别用红，橙，黄颜色的点来表示。

n_samples为整数时，表示一共有多少个散点，那么这些点在所有的集群之间平均分布，n_sample=50,而centers=2，那么这50个点在两个中心之间平均分布，每个中心所在的cluster的点的个数为50/2=25。

Centers: int or array of shape[n_center, n_features],optional

产生的中心点的数量，或者固定的中心点的位置坐标。

如果N_samples是整数但是又没有定义centers的个数，那么自定义为3个centers。

如果n_samples是矩阵的形式，那么centers必须为设置为空值（None)或者和n_sample长度一样的矩阵。

random_state: int, randomstate instance, default=None

这个参数在之前文章里面讲过的，要让你的随机的结果复现，就需要设置一个这个的参数。

Return_centers:bool,optional(default=False)

该参数为True时，make_blobs的返回值中会返回每个集群的中心点。

Cluster_std: floot or sequence of floats, optional(default=1.0)

The standard deviation of the clusters. 集群的标准差，标准差越小，数据越集中于自己的中心点。

Make_blobs 返回的值：

X: array of shape [n_samples, n_features]

The generated samples.产生的点的x,y坐标。

Y: array of shape[n_samples]

The integer labels for cluster membership of each sample.产生的每个点的标签，红颜色和黄颜色各一个标签，对应的值非0即1。如果有多个标签，假设有n个，那么这个y值的取值为[0,1...n-1]。

Centers : array , shape[n_centers,n_feature]

The centers of each cluster. Only returned if return_center=True。每个簇（cluster)中心点（centers)的坐标，只有make_blobs里面的return_centers参数设置为True时才会返回Centers的坐标。Random_state取不同值时，中心点的坐标也会随着不同，所以有时候为了让结果复现，也就是产生的中心点的坐标与上一次使用make_blobs function产生的一样，这里最好设置一下random_state。

from sklearn.datasets.samples_generator import make_blobs

X, y,C = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std = 0.30, return_centers =True)

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

在这个例子中要将这两个cluster分开来，可以直接do by hand，

xfit = np.linspace(-1, 3.5)

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

plt.plot([0.6], [2.1], 'x', color='red', markeredgewidth=2, markersize=10)

for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]:

plt.plot(xfit, m * xfit b, '-k')

plt.xlim(-1, 3.5)

Numpy.linspace

(start,stop,num=50,endpoint=True,retstep=False,dtype=None,axis=0)‍

numpy.linspace() 返回区间在[start,stop]，间隔均匀的num个数据点，

Start:array_like, the starting value of the sequence.区间的左端点。

Stop: array_like the end value of the sequence.区间的右端点。

Num: 在[start,stop]区间内产生的点（sample)的个数，自定义为50个。

Matplotlib.pyplot.scatter 画散点。

Matplotlib.pyplot.plot(scalex=True,scaley=Ture,**kwargs)‍

Fmt=’[marker][line][color]’

可以看到要将两组数据用直线分开可以有很多不同的直线，上图中画了三条直线，均可以将这两个(cluster)完全分开，这三条直线的（斜率，截距）分别为（1，0.65），（0.5，1.6）和（-0.2，2.9）这些直线的宽度都是零，我们可以给这些直线画一个给定宽度的margin，使灰色区域的边界正好接触到最近的cluster中的点。

xfit = np.linspace(-1, 3.5)

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:

yfit = m * xfit b

plt.plot(xfit, yfit, '-k')

plt.fill_between(xfit, yfit - d, yfit d, edgecolor='none', color='#AAAAAA',

alpha=0.4)

plt.xlim(-1, 3.5);

那么这三条直线中，哪条直线是最优的解呢？我们希望对于新加入的点，仍能能有较好的划分能力，在三条直线中，斜率为1或-0.2的两条直线容易把新加入的点划分到另一方区域内。

比如对于图中红色的x,斜率为-0.2的那条直线容易把它划分到黄颜色点的簇(cluster)中,而对于其他新加入的点，如果新加入的点的横坐标(x)超过三条直线交叉点的横坐标，此时很容易被斜率为1的直线将属于红色的簇（cluster)的点划分到黄色的cluster中，由此看来，只有中间那条线具有很好的容错能力，与它平行的两条灰色区域边界所围成的区域比其他两条直线拥有更大的margin。

在支持向量机(support vector machines)中，这条能够使灰色区域拥有最大margin的直线（上图可以看到最中间这条直线的灰色部分宽度最宽）就会被选择成为我们的最优模型。由此，支持向量机（support vector machines)可以看作是这种最大化margin时的estimator(中文叫算子)的一个例子。

下面我们使用scikit-learn的support vector classifier（SVC） 在上面那些数据上来训练一个SVM 模型。为了避免过于拟合或拟合不够充分，会在求解

最小值的过程种引入惩罚参数C。

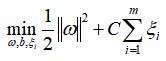
C>0称为惩罚参数，C值越大，容许的误差越小，C值过大时，容易出现过拟合，过小则出现欠拟合。在这个例子中，对于两个簇(cluster)，可以明显区分边界时，我们要求这个边界非常地有原则，泾渭分明，也就是边界very hard，此时可以把C设置为一个非常大的值。

from sklearn.svm import SVC # "Support vector classifier"

model = SVC(kernel='linear', C=1E10)

model.fit(X, y)

sklearn.svm.SVC

(*, C=1.0, kernel='rbf', degree=3, gamma='scale', coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape='ovr', break_ties=False, random_state=None)‍

SVC:support Vector Classification.

C:float, default=1.0 C为刚刚提及的惩罚参数，这里为满足划分地边界非常清晰，所以给C取值为C=1E10。

Kernel{'linear','poly','rbf','sigmoid','precomputed'},default='rbf'。

Specifies the kernel type to be used in the algorithm.

对于输入空间中的非线性分类问题，可以通过非线性变换将它转化为某个维特征空间中的线性分类问题，在高维特征空间中学习线性支持向量机。 由于在线性支持向量机学习的对偶问题里，目标函数核分类决策函数都只涉及实例核实例之间的内积，所以不需要显式地指定非线性变换，而是用核函数替换当中的内积。目前这里还是线性划分，所以kernel=’linear’,关于非线性的，下面待会儿会讲到。

Kernel函数的选择可以参考下面这个连接：

http://crsouza.com/2010/03/17/kernel-functions-for-machine-learning-applications/

Degree:int,default=3

这个参数仅适用于polynomial kernel多项式的维度，一次函数，二次函数，三次函数等，对于其他kernel，这个参数不适用。

Coef0:float, default=0.0

kernel function 中的独立项，仅对 kernel = 'poly'或 'sigmoid'时才有用。

gamma{‘scale’, ‘auto’} or float, default=’scale’

Kernel coefficient for ‘rbf’, ‘poly’ and ‘sigmoid’.

gamma这个参数是否具体存在要看你使用的是什么样的核函数（kernel）,在kernel参数的介绍中那个链接里面可以发现有些kernel里面是含有gamma这个参数的。

以Gaussian Kernel为例子做个简短的说明：

图中

值越大，高斯分布越扁平，对于所有的X更为雨露均沾，

（gamma）值越小，那么这个模型它就不能提取到数据里面更为复杂的部分，也是更具有特征性的那些部分，因为向量机的影响范围包含了整个训练集。与此同时，对于单一的training example，它的影响范围越广，它的训练和预测的速度也会慢下来。

如果gamma值非常大，支持向量的影响范围的半径（radius of the area of the influence)将会只包括支持向量本身，这时防止过拟合而设立的C值起到的作用就会变得很小。

Gamma 和C的取值也需要自己trade-off 一下，下图为在不同的gamma和C取值下，模型对两个cluster的分类情况。

sklearn.svm.SVC(gamma=)里面，如果gamma='scale'(default)，那么在计算时，gamma的值为1/（n_features*X.var())。如果 gamma='auto'，计算时gamma的值为1/n_features。

为了更好地可视化，下面定义一种快速的function用来画SVM的决策边界（decision boundaries）.

def plot_svc_decision_function(model, ax=None, plot_support=True):

'''Plot the decision function for a two-dimensional SVC'''

if ax is None:

ax = plt.gca()

xlim = ax.get_xlim()

ylim = ax.get_ylim()

# create grid to evaluate model

x = np.linspace(xlim[0], xlim[1], 30)

y = np.linspace(ylim[0], ylim[1], 30)

Y, X = np.meshgrid(y, x)

xy = np.vstack([X.ravel(), Y.ravel()]).T

P = model.decision_function(xy).reshape(X.shape)

# plot decision boundary and margins

ax.contour(X, Y, P, colors='k',

levels=[-1, 0, 1], alpha=0.5,

linestyles=['--', '-', '--'])

# plot support vectors

if plot_support:

ax.scatter(model.support_vectors_[:, 0],

model.support_vectors_[:, 1],

s=300, linewidth=1, facecolors='none');

ax.set_xlim(xlim)

ax.set_ylim(ylim)

Matplotlib.pyplot.gca: get the current Axes instance on the current figure matching the given keyword arguments, or create one。

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

plot_svc_decision_function(model)

画出如下图：

上图可以看出得到的分割线使得这两群点中间的margin最大。有些点正好在直线上面。在Scikit-Learn中，那些正好在边界的点组成了我们的support vector，并且存储在support_vectors_attribute中：

model.support_vectors_

对于非线性关系，可以通过定义多项式和高斯基本函数，将数据投影到高维度空间，由此可以使用线性classifier拟合非线性关系。

三、支持向量机处理非线性关系问题

from sklearn.datasets.samples_generator import make_circles

X, y = make_circles(100, factor=.1, noise=.1)

clf = SVC(kernel='linear').fit(X, y)

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

plot_svc_decision_function(clf, plot_support=False)

Sklearn.datasets.make_circles

(n_sample=100,*,shuffle=True,noise=None,random_state=None,factor=0.8)‍

Make_circles用来在二维平面上产生一个大的circle，该circle里面包含一个小一点的circle.

N_samples: 如果为偶数，外圈和内圈点的数量一样多；如果为奇数，内圈比外圈多一个点。

Factor:0<double<1(default=.8)

Scale factor between inner and outer circle.

在其他情况不变时，Factor 设为不同值的图如下：

Noise: double or None (default=None)

Standard deviation of Gaussian noise added to the data.

在其他参数不变的情况下，noise设为不同值时的图像如下：

由上面一系列图片可以看到，使用线性（直线）去划分非线性（中间一个圈，外面一个圈）的数据得到的结果并不理想，在二维平面上使用线性的可能永远无法将这两类点分开，那我们如何将这些点投影到更高维度才足以使用线性分开呢。举个简单的投影例子，我们可以使用计算一个集中在中间的 radial basis function。

radial basis function: a radial basis function(RBF) is a real-valued function whose value depends only on the distance between the input and some fixed point, either the origin. --wiki

对于在有限维度向量空间中线性不可分的样本，我们将其映射到更高维度的向量空间里，再通过间隔最大化的方式，学习得到支持向量机，就是非线性 SVM。

我们用 x 表示原来的样本点，用

表示 x 映射到特征新的特征空间后到新向量。那么分割超平面可以表示为：

。

对于非线性 SVM 的对偶问题就变成了，在三维空间，仅使用一个平面就能将其很好地分类：

r = np.exp(-(X ** 2).sum(1))

然后你可以使用下面的代码查看：

from mpl_toolkits import mplot3d

def plot_3D(elev=30, azim=30, X=X, y=y):

ax = plt.subplot(projection='3d')

ax.scatter3D(X[:, 0], X[:, 1], r, c=y, s=50, cmap='autumn')

ax.view_init(elev=elev, azim=azim)

ax.set_xlabel('x')

ax.set_ylabel('y')

ax.set_zlabel('r')

interact(plot_3D, elev=[-90,30, 90], azip=(-180, 180), X=fixed(X), y=fixed(y));

也可以自己计算一个z坐标，然后画一个三维的，比如刚刚讲的把上面的二维散点投影到三维，我们可以给一个z轴，使这些散点的z轴的值与二维图像上的散点到原坐标（0，0）的距离呈正关系，这里我们定义：

X为上面那些散点的x,y坐标，下面代码使用上式生成z坐标。

import pandas as pd

df=pd.DataFrame(data=X,columns={'x','y'})

df['z']=(df['x']**2 df['y']**2)**0.5

然后使用plotly画三维图像（记得先在anaconda prompt里面安装：pip install plotly）：

import plotly

import plotly.graph_objs as go

plotly.offline.init_notebook_mode()

trace=[go.Scatter3d(x=df['x'].tolist(),y=df['y'].tolist(),z=df['z'].tolist(),

mode='markers',marker=dict(size=6,color=y,colorscale='Viridis'))]

fig=go.Figure(data=trace)

fig.show()

color=y中y就是之前画的100个二维散点的时候给他们的分类标签，0或1值，这里对不同的类用不同的颜色区别。那么这个从x,y得到z的过程就是一个核函数的功能。

录了一个小小的video，小伙伴们感受一下将二维投影到三维后的效果：

上图可以看到投影之后我们很好地将这两类不同颜色地点分开来，只需要在中间插入一个平面（比如说z=0.5）就可以很easy地将两类分开。

如果我们这个投影project的basic function没有选择好，那么这个分离的效果可能就不那么明显了。

比如下面这种情况就需要用polynomial kernel来mapping（映射）

插入一个video：

每对点的前后转换过程叫做内核转换。

这种策略存在潜在的问题，投影N个点到N维，会随着N的增大使得运算量相当庞大，有一种过程可以替代掉这种一对一的映射，把它叫做kernel trick, 比如上面讲的

公式，SVM里面内置了这样的kernel trick, 这也是SVM强有力的原因之一。

下面看看如何使用SVM的内置kernel trick，其中kernel='rbf'。

clf = SVC(kernel='rbf', C=1E6)

clf.fit(X, y)

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

plot_svc_decision_function(clf)

plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],

s=300, lw=1, facecolors='none')

Kernel='rbf'中的rbf：radial basic function，使用方式和其他的model一样，大致形式都是model.fit(X,y)。

SVC.fit(self,X,y[,sample_weight]): fit the SVM model according to the given training data.

通过使用这种kernelized 的SVM模型，学习到了非线性决策边界，得到的下图很完美地区分了这两组非线性关系的点。

四、关于软边界

左图为硬边界，右图为软边界，软就是模糊，不清楚的意思。硬边界有明显的界限，而软边界里面，就会有部分互相参杂，那么互相参杂多少，这个容错的范围多大，也是由参数来确定的。

刚刚提及的都是边界很清晰的，可以将两类划分，有时候，这两种不同颜色的散点的边界并没有那么清晰，允许一部分点互相掺杂。比如当你碰到下面的这种情况时：

X, y = make_blobs(n_samples=100, centers=2,random_state=0, cluster_std=1.2)

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

通过mak_blobs人为产生了如上图的数据，下面用SVC线性划分这两个类别，因为边界不是很清晰，所以这里控制惩罚程度的C的值，不会像最初那样设置得很大，而这个容错的范围也由C的值确定，下面是SVM里面C分别为10和0.1的结果的图像：

X, y = make_blobs(n_samples=100, centers=2,random_state=0, cluster_std=0.8)

fig, ax = plt.subplots(1, 2, figsize=(16, 6))

fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)

for axi, C in zip(ax, [10.0, 0.1]):

model = SVC(kernel='linear', C=C).fit(X, y)

axi.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

plot_svc_decision_function(model, axi)

axi.scatter(model.support_vectors_[:, 0],

model.support_vectors_[:, 1],

s=300, lw=1, facecolors='none');

axi.set_title('C = {0:.1f}'.format(C), size=14)

C=0.1有部分点进入了两个cluster的support vector之间，而当C=10的时候没有。

,