黎曼求和法（我们用求和原理表示黎曼和的本质原理）

求和(或sigma符号)允许我们在一个表达式中写出一个长长的求和公式。虽然求和符号在整个数学(特别是微积分)中有很多用途，但我们要解决的是如何使用它来写黎曼和。

用求和符号来表示黎曼和的例子

假设我们在X=0.5和X=3.5区间上逼近f(x)=√x曲线下的面积

现在我们将上述区间分为四个相等的部分，并使用求和符号来表示这四个相等的细分的区间，这就是我们所说的黎曼和（这里的相等指的是X上的等距划分）

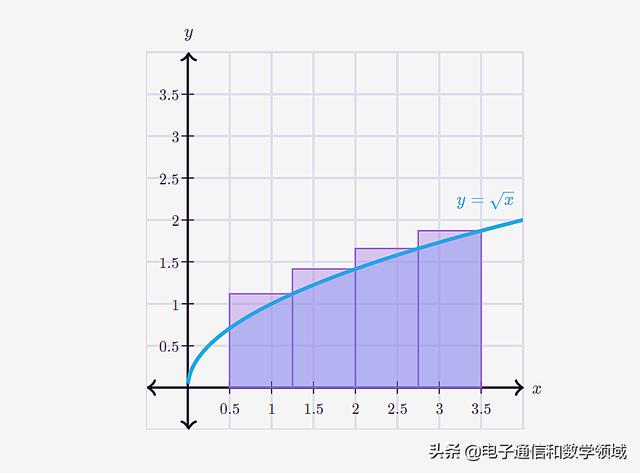
让 A(i)表示第i个近似矩形的面积

整个黎曼和可以写成：

我们现在要做的是找到 A(i)的表达

整个区间宽度是3，我们想要将其划分为4个相等部分，所以每个矩形的宽度就是3/4=0.75，每个矩形的高度就是右端点在√x的取值

如下让xi表示每个长方形的右端点坐标值，我们从X=0.5，间隔为0.75开始，并不断循环

因此xi的坐标公式就是0.5 0.75i，它在Xi的取值就是

所以我们得到了矩形 A(i)面积的一般表达式

现在剩下的就是把从1到4的矩形的表达式的值加起来

总结：用求和符号表示黎曼和的过程

想象一下我们想在区间[a,b]内用n等分逼近f(x)图下的面积

定义ΔX: 用Δx表示每个矩形的宽度，Δx=(b-a)/n

定义Xi: xi表示每个矩形的右端点，然后xi=a Δxi

每个矩形的高度就是f(xi)，每个矩形的面积就是Δxf(xi)

对矩形面积求和：现在我们使用求和符号来表示所有矩形的面积

值得一提的是：左黎曼和右黎曼和是不同的

当我们写一个右黎曼和时，我们取得i是从1到n的值

然而，当我们写一个左黎曼和时，我们取得i值是从0到n-1(这将给出每个矩形左端点处的f值)。