光流估计深度学习与传统算法比较（基于GA-BP神经网络对不可避免漏失水量的确定）

摘 要：

为了分析管网漏损影响要素和供水管网不可避免漏失水量之间存在的复杂联系及对应关系，建立适用于我国不可避免漏失水量的确定方法。通过采集、筛选实际管网的漏损统计数据，对独立计量区域(DMA)展开夜间最小流量分析，并分析研究区域内管网的影响因素，将管龄、管材、用户数量及管网压力设定为相关影响参数。在此基础上，分别建立BP神经网络模型以及经过遗传算法优化后的BP神经网络模型(GA-BP神经网络),并对优化前后二者神经网络模型拟合结果对比分析。最终将优化后的模型应用于不同DMA进行漏损分析。结果显示，优化后的BP神经网络不仅训练效率更高，且误差平均降低了3.02%。将该模型应用于实际管网三个不同DMA时，可以发现DMA内均存在可控漏损水量，以经济可行为前提，分别可节约水量10 512 m3/a、12 702 m3/a、37 580.4 m3/a。研究成果可为DMA漏损控制提供参考。

关键词：

BP神经网络;遗传算法;可行性评估;不可避免漏失;线性回归分析;人工智能算法;DMA;影响因素;

作者简介：

王俊岭(1973—),男，副教授，博士，主要从事节水技术、管网优化控制等研究。E-mail:18813070523@163.com;

*胡颖梦(1996—),男，硕士研究生，主要从事管网漏损控制等研究。E-mail:17858285940@163.com;

基金：

国家水体污染与治理科技重大专项课题(2017ZX07501-002-05);

引用：

王俊岭，胡颖梦，张昕喆，等． 基于 GA-BP 神经网络对不可避免漏失水量的确定［J］. 水利水电技术( 中英文) ，2021，52( 12) : 201-211.

WANG Junling，HU Yingmeng，ZHANG Xinzhe，et al． GA-BP neural network-based determination of unavoidable annual real losses from water supply pipeline network［J］. Water Ｒesources and Hydropower Engineering，2021，52( 12) : 201-211.

---

0 引 言

供水管网漏损是困扰所有供水企业的问题，漏损可以定义为在用户计量点之前，所有类型的泄漏、爆裂和溢出造成的水损失量。管网漏损是由缺乏主动漏损控制(ALC)、运行压力过大、操作和维护不良、振动和交通负荷以及管道腐蚀等因素综合导致。随着政府对管网漏损的加强重视，出现了越来越多先进的技术、方法与措施。

然而在技术不断革新的同时，出现了技术无法得到有效应用等问题，其中关键一方面在于漏损评价，漏损评价是有效控制漏损的基础。漏损评价中的关键点是漏损评价指标的选择，指标的是否合适决定了漏损情况能否得到真实反映。1997年，国际水协 (IWA)工作小组提出了基础设施渗漏指数(ILI),随着国内外对于漏损研究的深入，产销差率、泄漏性能指数(LPI)等指标也被不断提出并通过实践应用纳入评价体系中去，GIOVANNA建立了泄漏性能指数(LPI),强调LPI值和漏损值之间的线性相关性。张现国在国内应用供水管网漏失指数(ILI)并进行了实例计算。代焕芳在分别分析了真实漏失量、产销差率、ILI等指标后，建议国内引入ILI概念来进行管网漏损评价。随后提出了真实漏失水量评价指标——供水管网背景漏失指数(BLI)。

ILI是目前美国环境保护署(EPA)、美国水务协会(AWWA)和国际水协会(IWA)共同认可的衡量真实漏失的可靠指标点之一。ILI定义为当前物理漏失水量(CARL)和系统内不可避免漏失水量(UARL)之间的无量纲比率,其中UARL(Unavoidable annual real losses)意味着在当前背景条件下，无论是技术还是经济层面都无法避免的供水系统理论最小漏失。因此通常将UARL视作基准值评价管网漏损情况，明确区域内漏损现状的可提升空间。不可避免漏失水量的计算主要分为实测与计算两种方式，实测法指在检漏水平高、计量准确且无偷盗水现象的DMA(District metering area, 即独立计量区域)中，可以将夜间最小流量视作夜间居民正常用水量与DMA不可避免漏失水量的和，因此得到公式UARL=QMNF-Q夜间居民。除此之外，国际水协提出了UARL经验计算公式，该公式系统性的将支干管长度、压力、连接点数等因素纳入研究范围，是目前为止国际通用最优的方法。董驹萍应用该公式与实测最小夜间流量数据进行对比，发现二者的差异颇大。同样，现有的研究表明,我国供水系统难以用IWA提出的经验公式照搬套用。分析原因，一是国内管网情况复杂，公式参数需要调整；二是公式中部分定义存在界限模糊问题，例如国内没有对公式中“评价区域内连接点数”有明确的标准定义，即需要根据管网不同情况重新定义选取。阅读国内现有的研究，发现大多学者为研究出适应国内现状的公式，展开了一系列探讨对参数进行修正以及重新定义，目前来看，经验公式在国内应用存在一定的难度,国内复杂的管网现状要求该经验公式需要结合更多的影响因素及其对应联系，或许能得到更为合理的确定方法。调研漏损方面文章，目前国内还没有学者对UARL进行建模模拟分析。因此，考虑提出一种新的方式，本文基于国内现状，希望通过建模对不可避免漏失水量进行模拟校核，试图得到更贴近现实的模拟值，支撑UARL的确定，从而为管网漏损控制评价提供数据支撑。

人工神经网络是当前最为流行的模拟预测方法，以结合数据分析与挖掘的方式，通过自身的非线性处理，在内部进行各个节点的权、阈值的调整修正，从而输出结果。其中BP神经网络更受学者们的关注，BP神经网络无论是理论方面或是性能都已经是极为成熟的，尤其是针对难以发现规律的样本库，通过特殊的网络构造以及强大的非线性映射的特点，恰好适用于挖掘UARL与多种漏损影响因素之间模糊的关系。BP神经网络在管网评价、漏损定位以及爆管预测等方面已有广泛应用，然而BP神经网络本身存在着局限性，主要原因在于其初始权、阈值的随机选取，容易导致网络不收敛或是陷入局部极值点，从而影响模拟效果。为了弥补以上缺陷，万盛萍提出可以利用遗传算法的特性，先进行寻优步骤，在此基础上，利用BP网络精准求解，既可以有效规避BP神经网络的局限性，又可以进一步提升模拟精确性。

本研究通过采集多个DMA的基础数据，剔除无效数据，运用拥有强大的数据处理能力与泛化能力的人工神经网络,构建了一种新型的不可避免漏失水量的确定方法——基于GA-BP神经网络的不可避免漏失水量模型，并通过实际的管网DMA进行模型的应用，得出相应的漏损评价，给出改进措施，达到优化漏损控制措施、节约水资源的目的。期待能够将此模型广泛应用于我国供水管网漏损评价中去，能够为进一步提升DMA漏损控制提供参考。

1 研究区域概况

1.1 研究区域简介

为了探清国内不可避免漏失水量的应用前景，本研究通过对实际DMA展开研究与分析，通过构建模型的方式对水量进行模拟，并以此作为指导漏损控制工作的依据。研究区域为我国南方X市某供水企业供水区域，共设有三座水厂，为该市生活、生产提供保障，供水总用户超40万户，日供水能力超过60万m3,管网总长约1 500 km。

该企业根据实地区域情况，按照分区规模、压力、分区完整性以及计量选择等原则进行了区域划分，在每个区域进出管装上智能水表，形成独立计量区域DMA,并建立了国际上先进的GIS系统与SCADA系统为一体的智慧供水管理体系，以此进行实时数据监测。

1.2 前期工作

对于不可避免水量的计算，本研究基于实际DMA出发，通过夜间最小流量(Minimum night flow, MNF)展开分析，MNF通常由夜间合法用水量以及夜间漏损水量两部分组成。因此，对DMA内的漏点进行彻底的排查检修的同时，结合压力调控，使得管网压力满足最不利点压力，此时的MNF可以视为由夜间居民正常用水量与不可避免漏失水量构成。通过以下步骤对数据进行确定：

(1)对DMA展开全面的检漏修漏，确保修复一切可检测到的漏点。

(2)确定MNF计量区间，根据国内外研究，并结合当地居民生活习惯将计量区间定为01:30—03:30。在此基础上，每间隔一分钟，进行一次流量数据采集，这样可以在计量区间内的某一瞬间取到夜间最小流量，此时可视作不存在夜间居民正常用水量，将此作为研究数据。

(3)为避免出现偶然性与极端性，连续取14 d流量并取均值，作为最终研究区域内的不可避免漏失水量。

在研究区域内，选取流量数据连续且合理的中型规模(用户数量1 000～3 000户)DMA,共36个DMA进行以上步骤，进行研究模拟，以此验证模型的精确性。最后，利用剩余三个保持现状的DMA,作为模拟研究后的实例应用，代入模型后，每个DMA可以得到模拟优化后的不可避免漏失水量(即当前管网条件下，可控制达到的最低漏损状态),与DMA当前实测的不可避免漏失水量产生对比，从而指导漏损控制工作。部分原始数据如表1所列。

1.3 影响因素

选取管网漏损影响因素作为构建模型输入的参数，为得到与管网漏损联系最密切的参数变量，需要就管网漏损的影响因素展开分析讨论。本研究前期利用灰色关联度法对研究区域内漏损的影响因素进行评价分析，得到结论：管材与管龄是影响最为显著的两个影响因素。

因此，首先确定管龄、管材作为模型输入主变量。在此基础上，考虑到用户数与管网供水量的密切关联，以及压力对于供水管网漏损的调节控制效果，另外增加两个变量：用户数N和管网平均压力P。模型的输出即设为不可避免漏失的水量。

2 研究方法

2.1 原理介绍

1986年，以RUMELHART为代表的研究者提出了一种按照误差逆向传播算法训练的神经网络—BP(back propagation)神经网络的概念，核心思想是正向输出与误差的逆向传播，不断迭代计算从而得到最优输出。BP神经网络分为输入、隐含、输出三个层次，如图1所示，各个层次分别由多个节点构成，各个层次之间由不同的权值连接ωki、ωij。

图1 BP神经网络结构

隐含层第i个神经元输出值

正向传播输出层神经元j的输出值

逆向传播误差定义的函数为

式中，n为样本数；ΔSv为样本值与模拟值的差。

GA-BP神经网络模型的构建分为以下三块内容：(1)确定各项参数以及输入与输出量，建立结构；(2)根据遗传算法全局搜查的特性，主动寻优，优化初始权值和阈值；(3)将寻优后的结果重新赋予回到构建的BP神经网络中去，开始迭代计算、模拟输出，如图2所示。

图2 GA-BP神经网络原理

2.2 基于GA-BP神经网络不可避免漏失水量计算的可行性评估

2.2.1 强大的数据处理能力

不可避免漏失水量的确定需要基于复杂多样的基础管网信息，GA-BP神经网络利用其特有的大规模并行、分布式储存和处理自适应性等技术,相对于传统耗时耗力且复杂的模型，无需过多的设定与数理支撑，可以在给定的数据库中，找到潜藏的规律，并建立合理联系。

2.2.2 从数据出发的客观性结论

对不可避免漏失水量进行建模预测，首先需要确定输入参数以及对应权值和阈值，GA-BP神经网络通过对样本数据进行训练，利用其全局搜索能力，求解最优初始权值与阈值[19]反馈回神经网络中，结果源于数据，避免了人为主观干预与随机初始值带来的误差，极大地增强了结论的客观性。GA-BP神经网络应用流程如图3所示。

图3 GA-BP神经网络应用流程

3 模型对比及实际应用

3.1 模型参数变量的确定

根据对研究区域现状与影响因素分析，确定管龄、管材(分为铸铁管与非铸铁管)、用户数N和管网平均压力P共五个输入参数，不可避免漏失水量作为模型的唯一输出。

3.1.1 确定神经网络层次结构与节点数

BP神经网络的性能优劣取决于网络结构中隐含层数和隐含层节点个数。最直观的影响即当隐含层节点数设置过少，会降低训练精确度；当取用的节点数量相应增多时，可以起到提升训练精确度的效果。但节点数的设置也存在过犹不及的现象，若选取的节点数太多，会产生神经网络逼近能力过强的情况，而弱化了很重要的泛化能力。因此，节点数的设置存在一个适宜的区间，HO等、邵圆媛发现，一个三层BP神经网络只需要一个隐含层，即可以通过对该隐含层的节点数进行调整，从而映射任意连续函数，且满足精度需求。因此，本试验仅选取一个隐含层。

(1)输入层。

本模型的输入参数分别为管龄、管材、用户数以及管网平均压力，其中根据区域管网特性，管材分为铸铁管与非铸铁管两个变量，则节点数定义为5。

(2)输出层。

输出即不可避免漏失水量，故节点数定义为1。

(3)隐含层。

至今为止，隐含层节点个数的确定还未产生一般规律性计算方式[23],目前大多选择通过经验公式计算得到范围值如下

式中，n为隐含层节点个数；m为输入层节点个数；a为输出层节点个数；l为1到10的随机整数。

然后进行试凑整法来计算隐含层节点个数，当均方误差(MSE)达到最小时，对应的节点个数即为最佳。计算得到隐含层节点数的范围为4到13。经过不断地往复训练，结果显示：当MSE达到最小值时，节点个数为10,即理想的节点数。

3.1.2 设置神经网络其余参数

训练参数具体如表2所列。当满足最高训练次数、最小误差值、梯度大小或者满足验证次数所设定的参数值的情况时，即代表完成训练，并自动结束训练。

以MATLAB为平台，在所有的36组DMA数据中，随机抽取五组作为测试用的样本数据，其余的DMA数据则用于训练神经网络。为消除数量级、单位等影响，采用函数mapminmax对输入、输出数据进行归一化

式中，y为初始数据；ymin为最小值；ymax为最大值。

3.2 设置遗传算法优化BP神经网络控制参数

(1)编码。

随着各种算法的深入开发研究，编码的方式多种多样，其中二进制编码使用频率较高，应用范围也较广，但可能导致编码过长，从而会存在影响神经网络学习精度的可能性。本文选择实数编码，计算编码长度L,公式如下

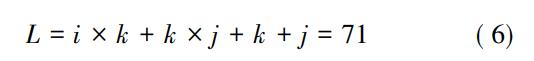
式中，i为输入层节点数；k为隐含层节点数； j为输出层节点数。

(2)种群规模。

种群规模的设置不存在严格的标准，在适宜区间范围内10～200之间选择即可，本研究通过对不同种群规模进行大量尝试，最终考虑拟合效果，选定为10。不同的数据样本建模应当进行重新尝试与选取，在满足精确度前提条件下，种群规模应当选取足够大以避免结果陷入局部最优解。

(3)适应度。

适应度通过实际值与模拟值的误差绝对值之和来表示。

(4)遗传操作。

选择操作为轮盘赌法(适应度比例法)。在交叉操作中，交叉概率取0.8(概率大小不仅与收敛速度有着紧密的关联性，而且可以减小非最优解输出的可能性)。在变异操作中，本试验中取0.1,处于一般经验值之间，避免过大或过小。

(5)终止进化代数一般在50～100之间选取，本试验选定为100。

对经过遗传算法优化后的BP神经网络，进行样本数据训练，得到适应度变化曲线(见图4)。由图4可知，在0～22代内，适应度随着迭代次数的不断增多而迅速下降，随后则趋于直线，说明在0～22代内，适应度在得到持续的优化，直至第22代，达到个体的最佳适应度，也说明了本试验取用100代的进化代数是可行的。最后将22代的最优个体输出并作为GA-BP神经网络模型的初始权值和阈值。

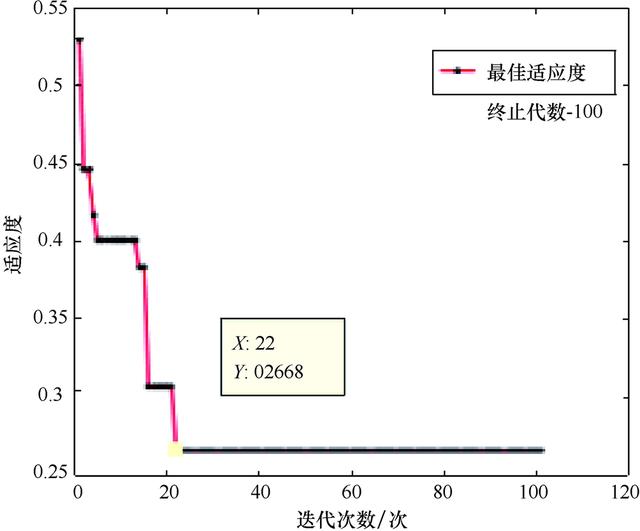
图4 适应度变化曲线

3.3 应用对比

对二者神经网络模型同步开展训练，图5为训练完成界面，并得到相对应的误差曲线变化图如图6所示。根据表1,训练完成的标志即误差满足设定值，结合图6训练样本误差曲线图，可以看出BP神经网络经过训练后的MSE值会随之相应降低，尤其是前5次训练效果显著，之后均方误差缓慢降低，最终在41次训练后，误差值为9.675×10-5,完成训练。而GA-BP神经网络相比较，在效率上得到了极大的提升，仅仅通过12次训练，误差已经达到8.752×10-5,完成训练。

图5 训练结束示意

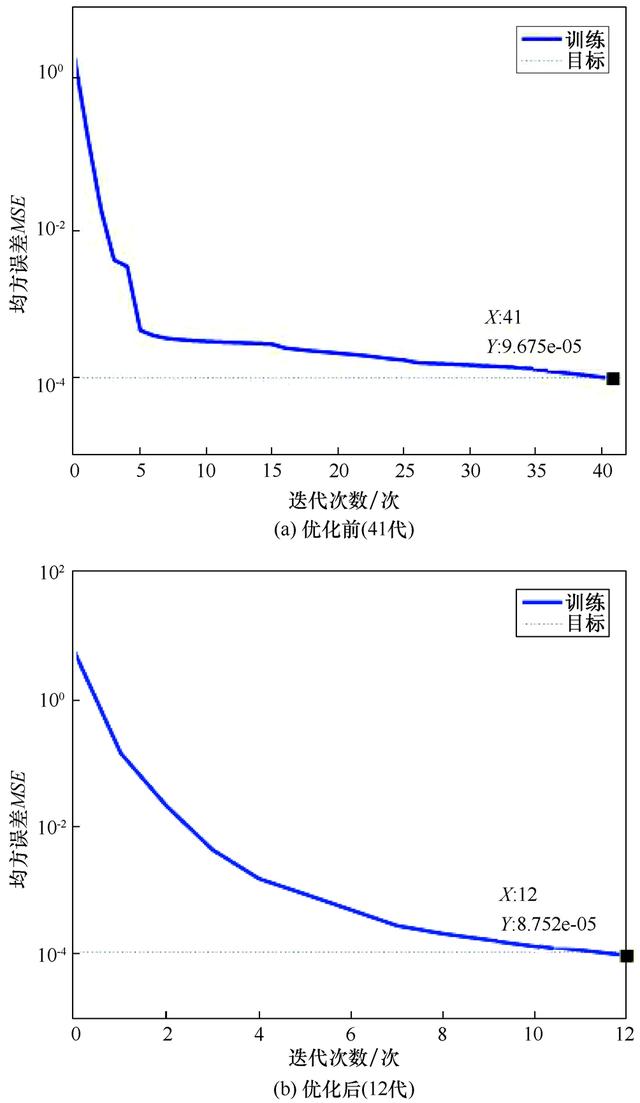
图6 训练误差曲线

对GA-BP神经网络和BP神经网络的模拟效果进行对比分析。对5组随机样本数据，编号1—5,展开拟合效果分析，五组模拟结果曲线分别如图7所示。从图7可知，对比第一组样本的模拟输出值，BP神经网络模拟值更为准确，但二者模拟值与实测值的误差均较小，剩余四组的结果均表明GA-BP神经网络的模拟值更加接近实测值，可以初步认为，GA-BP神经网络模拟值与实际值之间更加贴合。

图7 模拟曲线对比

3.4 模拟结果分析

从误差角度进行分析，GA-BP神经网络对于测试样本的数据模拟精确度上，显然有了一定的提升。平均误差在BP神经网络的基础上降低了3.02%,最大误差降低了5.16%,最小误差降低了1.07%,模型拟合的精度得到显著提升；从神经网络训练效率角度，GA-BP神经网络中，综合遗传优化以及网络训练，对样本数据共计进行迭代运行34次，比BP神经网络的41次迭代训练更高效。

为进一步对比模型效果，分别开展线性回归分析测试，如图8所示。显然GA-BP网络的最佳拟合曲线与目标曲线更为贴近，BP神经网络和GA-BP神经网络测试样本数据的线性回归直线分别为Y=0.912 4X 0.311 6、Y=0.976 8X 0.050 2,GA-BP神经网络决定系数R2=0.993 4大于BP神经网络R2=0.960 6,说线性回归直线的拟合度更高，也意味着模拟值更为精确。

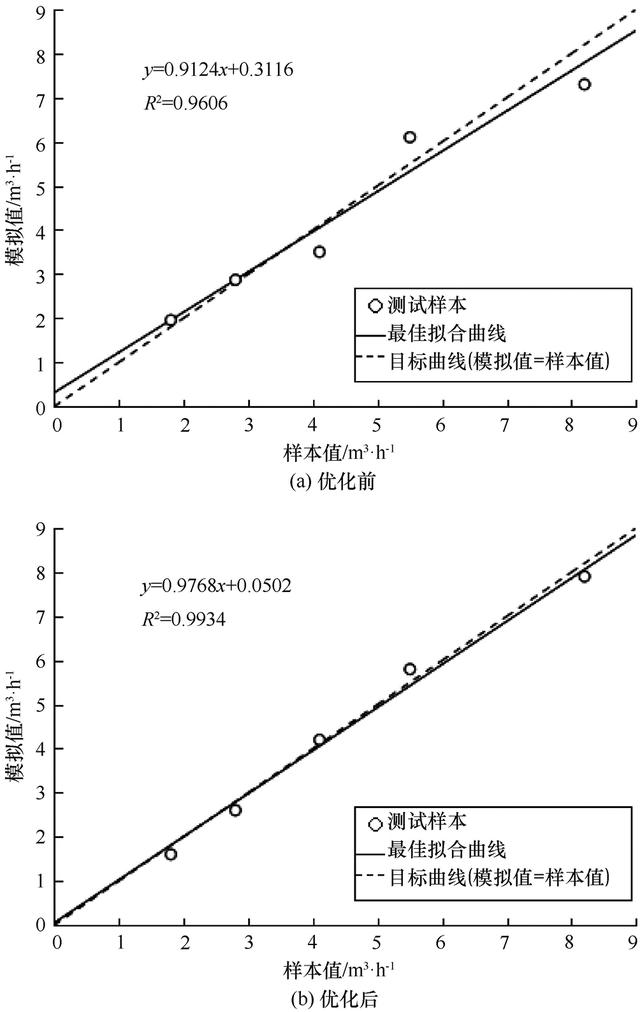
图8 线性回归对比

综上，无论是从相对误差的角度还是从线性回归精确性方面，GA-BP神经网络模型都是一种更为优势的方式，可以更好的对不可漏失水量展开模拟。通过上述一系列对比研究分析，得到以下结论：(1)BP神经网络满足了本研究的初步期待，确实可以满足对UARL的模拟，结果与实测值相当接近，可以为实际管网的评价提供科学数据支撑。(2)遗传算法对于BP神经网络的训练速度，以及结果的输出上均有正向提升，通过GA-BP神经网络对UARL的确定是更优选择。

3.5 实际应用

3.5.1 模型应用

将构建的模型应用于X市某DMA,并对其展开漏损评价，给出相应控制措施及建议。DMA基础信息如表4所列。

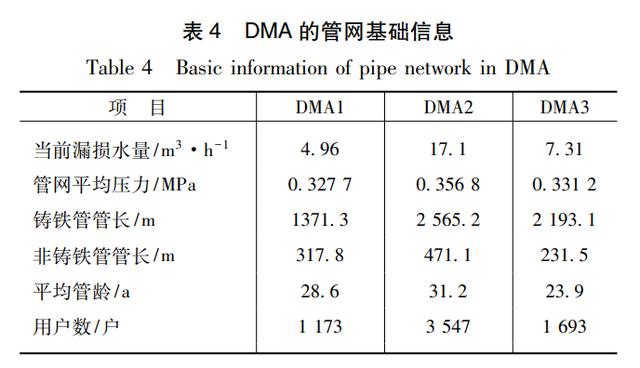
将上述基础信息代入模型进行计算。此外，由于压力控制作为管网漏损控制主要措施之一，为了探究其对于当前DMA区域的控制效果，将目前供水压力降低0.01 MPa, 作为压力调控措施后的目标压力值，再进行计算。模拟结果如图9所示。

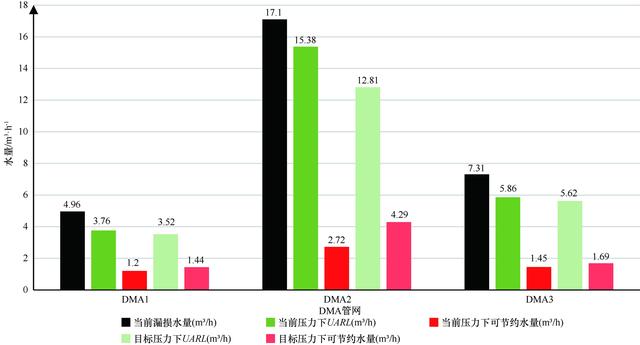
图9 模拟结果

3.5.2 结果分析与建议

为了对比当前该区域的可节约水量(即通过检漏修漏、压力调控等措施控制漏损，以达到该区域内最低漏失水平，再用当前漏损水量与UARL值作差，得到可节约水量),将结果通过百分比进行展示如图10所示。

图10 可节约水量占比

根据图10结果展开分析，并分别提出漏损控制措施建议及预期效果。

以DMA1为例进行计算，根据节1.1提到的前期工作，对DMA进行彻底的明、暗漏检修措施后，且在适当的压力下，可以认定此时该区域的漏失达到最理想状态，因此DMA1在当前压力下年度可节约水量=1.2×24×365=10 512 m3。同理DMA2、DMA3在当前压力下每年可分别节约水量23 827.2 m3、12 702 m3。而在目标压力下，DMA1、DMA2、DMA3分别可节约水量为12 614.4 m3、37 580.4 m3、14 804.4 m3。

由图10可知，DMA1与DMA3二者情况类似，当前区域内漏损水量明显大于UARL,需要对相关DMA采用主动漏损控制措施，开展彻底的检漏并及时修复漏点，同时压力调控起到的控漏成效较低，代表此时管网运行压力相对合适，若增加压力控制，此时控漏的经济效益很低甚至导致负经济效益，所以对DMA1、DMA3均采取主动控漏的方式，可以分别达到降低24.19%、19.84%的漏损水量，预计可分别节水10 512 m3/a、12 702 m3/a。对应本研究章节1前期工作中的内容，重点需要增加这两个DMA巡检队伍检漏修漏强度，根据该区域的平均水价(当地水费分梯度计算，此处计算粗略取3元/t, 稍高于第一梯度)可以计算得到，每年DMA1、DMA3可以通过主动检漏的方式(无需额外投入)分别节约31 536元/a、38 106元/a。

在DMA2中，漏损水量明显大于UARL,同样需要主动控漏，可以降低15.91%的漏损水量。同时，该DMA在目标压力下，UARL值进一步降低，且降幅较大，说明压力调控在该DMA可以起到显著的控漏效果。通过主动控漏结合压力调控可将漏损水量进一步减少9.18%,达到综合降低25.09%的漏损水量。综上，需要通过结合主动控漏和压力调控措施，预计可节水37 580.4 m3/a。对于DMA2来说，不仅需要加强检漏修漏措施，还需要对区域内的压力进行调节。研究区域内并未出现缺压情况，当前的供水压力可以满足用户正常需求，且有一定空间可以下调，因此仅需安装一定数量的减压阀即可进行初步的漏损控制。若需进一步开展系统地分时段分区域调压，则需要建立压力反馈监测系统等，不适宜在单独DMA内进行，建议从整个大供水管网层面建立模型。综上，进行粗略的估计，DMA2至少可以节约100 000元/a。

通过在X市进行验证，利用GA-BP神经网络建模的方式对优化后的DMA进行不可避免漏失水量预估，从而与实测不可避免漏失水量进行对标，据此指导漏损，是一种可行的方案，可以为漏损评价提供一定数据支撑，也可以为DMA的漏损现状提供判断依据，估计区域内漏损可提升空间。且投资较小，成效立竿见影，适合在单独DMA区域内推广应用，用于管网漏损检验，指导管网漏损控制工作。

4 结论与展望

(1)本文通过结合遗传算法对BP神经网络进行优化，不仅可以有效提高模型训练效率，还在精度上有了一定的提升，平均误差在BP神经网络的基础上进一步降低了3.02%,证明GA-BP神经网络模型可以更好地模拟得出不可避免漏失水量。于是在管网基础信息一定的前提下，利用模型模拟出DMA可优化得到的不可避免漏失水量，与实测DMA的结果进行对比，来评价各DMA的漏损情况，并提出相应的漏损控制措施，结果表明对不同区域展开相应控漏措施，均有不同程度的节水成效，最大可节水37 580.4 m3/a。希望本文对UARL的确定方法可以为我国漏损控制工作提供新的衡量方式。

(2)本文选取了平均管龄、铸铁管管网长度、非铸铁管管网长度、用户数和管网平均压力五个参数作为模型的输入参数，从结果上看，较准确地得到了不可避免漏失水量模拟值，可以作为其他区域模型建立的参考。当然输入参数并不限于此，不同区域应当有不同的研究结论与输入参数，一定程度下，参数越多，反映的结论越接近现状，因此，希望更多学者可以开展更多元深层次的研究。

供水管网漏损控制是一个持续不断的工作，管网漏损从起初的杂乱无序，到现在的管理有方，从人工检漏到如今预警监测技术不断革新，漏损控制工作逐步向大数据时代融合，在此基础上进行数据的挖掘与分析，形成特定的结构与模型，从而辅佐漏损控制工作的决策与展开成为当前乃至未来的一个方向，因此，未来学者应当投入更大的精力到数据化模型构建的研究中去，以更加客观的数据化结论提供科学的依据。

---

水利水电技术（中英文）

水利部《水利水电技术（中英文）》杂志是中国水利水电行业的综合性技术期刊（月刊），为全国中文核心期刊，面向国内外公开发行。本刊以介绍我国水资源的开发、利用、治理、配置、节约和保护，以及水利水电工程的勘测、设计、施工、运行管理和科学研究等方面的技术经验为主，同时也报道国外的先进技术。期刊主要栏目有:水文水资源、水工建筑、工程施工、工程基础、水力学、机电技术、泥沙研究、水环境与水生态、运行管理、试验研究、工程地质、金属结构、水利经济、水利规划、防汛抗旱、建设管理、新能源、城市水利、农村水利、水土保持、水库移民、水利现代化、国际水利等。

,