九年级数学二次函数几何最值（九年级数学二次函数综合）

九年级数学：二次函数综合，等腰三角形存在性，动点坐标

香雪海教育

题目呈现

如图，在平面直角坐标系中，二次函数y=ax² bx--4(a≠0）的图象与x轴交于点A（--2,0）、C（8,0）两点，与y轴交于点B，其对称轴与x轴交于点D。

（1）求该二次函数的解析式。

（2）连接BC。在线段BC上是否存在点E，使得△CDE为等腰三角形？若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由。

（3）若点P（m,n）是该二次函数图像上的一个动点（其中m＞0，n＜0），求△BDP面积的最大值及此时点P的坐标。

解析：

（1）待定系数法。将A、C坐标分别代入二次函数解析式中，联解关于a、b的二元一次方程组，得a=1/4，b=--3/2。所以该二次函数解析式为y=1/4x²--3/2x--4=1/4（x一3）² 一25/4.

（2）分别以C、D、E为等腰三角形顶角的顶点，分三种情况考虑。

当CD=CE时，过点E作EF⊥x轴于点F。如下图所示。

∴EF∥y轴，

∴Rt△CEF∽Rt△CBO，

∴EF/BO=CE/CB=CF/CO。

而BO=丨yB丨=丨一4丨=4，

CE=CD=xC一xD=8一3=5，

CB=√（BO² CO²）=√（4² 8²）=4√5，

∴EF=5/（4√5）×4=√5。

∴yE=一√5。

CF=5/（4√5）×8=2√5。

∴OF=8一2√5=xE。

∴E（8一2√5，一√5）。

当DE=DC时，连接DB。如下图所示。

在Rt△ODB中，OD=3，OB=4，由勾股定理得DB=5。

而DE=DC=OC一OD=8一3=5，

可见DE与DB完全重合，点E与点B重合，故E（0，一4）。

当ED=EC时，过点E作EG⊥x轴于点G。如下图所示。

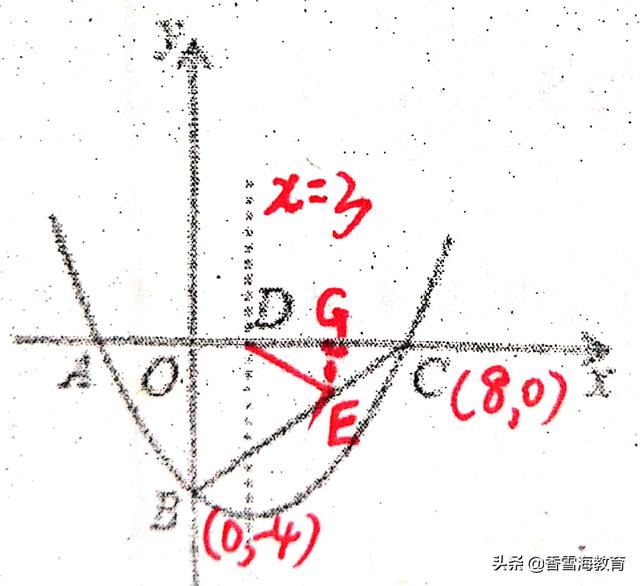
则DG=GC（等腰三角形三线合一性质）。易知Rt△CEG∽Rt△CBO，得EG/BO=CG/CO。其中CG=1/2CD=1/2（OC一OD）=1/2×（8一3）=2.5。

∴EG=2.5/8×4=5/4.∴yE=--5/4.

OG=3 2.5=5.5=11/2=xE。

∴E（11/2，--5/4）。

（3）过点P作PH丄x轴于点H。如下图所示。

S△BDP=S直角梯形OBPH一SRt△PHD一SRt△BOD=1/2[4 （一n）]m一1/2（m一3）（一n）一1/2×3×4=2m一3/2n一6。

∵点P在该二次函数图象上，

∴n=1/4m^2一3/2m一4。

∴S△BDP=2m一3/2（1/4m^2一3/2m一4）一6=--3/8m^2 17/4m=一3/8（m一17/3）^2 289/24。

∴当m=17/3时，S△BDP最大=289/24。此时点P（17/3，一161/36）。

此题对计算能力要求较高。

,