8年级实数知识点归纳整理（7数期中实数复习）

一．复习目标

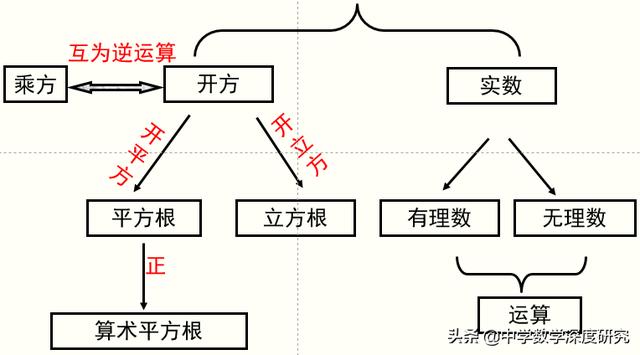
1.了解算术平方根、平方根、立方根的概念，会用根号表示数的平方根、立方根.

2.了解开方与乘方互为逆运算，会用平方运算求某些非负数的平方根，会用立方运算求某些数的立方根，会用计算器求平方根和立方根.

3.了解无理数和实数的概念，知道实数与数轴上的点一一对应，有序实数对与平面上的点一一对应；了解数的范围由有理数扩大为实数后，概念、运算等的一致性及其发展变化.

4.能用有理数估计一个无理数的大致范围.

二．知识网络

三．知识要点

2.实数与数轴上的点一 一对应.

数轴上的任何一个点都对应一个实数，反之任何一个实数都能在数轴上找到一个点与之对应.

3.实数的三个非负性及性质：

在实数范围内，正数和零统称为非负数。我们已经学习过的非负数有如下三种形式：（1）任何一个实数a的绝对值是非负数，即|a|≥0；（2）任何一个实数a的平方是非负数，即a²≥0；（3）任何非负数的算术平方根是非负数，即√a≥0 (a≥0).

非负数具有以下性质：（1）非负数有最小值零；（2）有限个非负数之和仍是非负数；（3）几个非负数之和等于0，则每个非负数都等于0.

4.实数的运算：

数a的相反数是－a；一个正实数的绝对值是它本身；一个负实数的绝对值是它的相反数；0的绝对值是0.

有理数的运算法则和运算律在实数范围内仍然成立.实数混合运算的运算顺序：先乘方、开方、再乘除，最后算加减.同级运算按从左到右顺序进行，有括号先算括号里.

5.实数的大小的比较：

有理数大小的比较法则在实数范围内仍然成立.

法则1. 实数和数轴上的点一一对应，在数轴上表示的两个数，右边的数总比左边的数大；

法则2．正数大于0，0大于负数，正数大于一切负数，两个负数比较，绝对值大的反而小；

法则3. 两个数比较大小常见的方法有：求差法，求商法，倒数法，估算法，平方法.

四．考点分析

考点1 开方运算

1．（2019春•鼓楼区校级月考）若方程（x﹣4）²＝19的两根为a和b，且a＞b，则下列结论中正确的是（ ）

A．a是19的算术平方根B．b是19的平方根

C．a﹣4是19的算术平方根D．b 4是19的平方根

【解答】∵（x﹣4）²＝19，∴x﹣4＝±√19，∴x₁＝4 √19，x₂＝4﹣√19，

∵a、b是方程（x﹣4）2＝19的两根为a和，且a＞b，

∴a＝4 √19，b＝4﹣√19，∴a＞0，b＜0，∴a﹣4＝√19，b﹣4＝﹣√19．

A．a是19的算术平方根，应改为a﹣4是19的算术平方根，所以错误；

B．b是19的平方根，应改为b﹣4是19的平方根，所以错误；

C．a﹣4是19的算术平方根，正确；

D．b 4是19的平方根，应改为b﹣4是19的平方根，所以错误．故选：C．

考点2 无理数

2．（2019春•潮阳区校级月考）在实数√5，22/7，π/2，√36，﹣1.414，3.14159265，0.1010010001……中，无理数有（ ）

A．3个B．2个C．1个D．0个

【解答】在所列实数中，无理数有√5，π/2，0.1010010001……这3个，故选：A．

【点评】此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，√6，0.8080080008…（每两个8之间依次多1个0）等形式．

考点3 实数的性质

考点4 实数与数轴

4．（2018秋•宁德期末）在如图所示的数轴上，表示无理数√π的点在A、B两个点之间，则数m不可能是（ ）

A．10 B．7 C．6 D．5

【分析】根据无理数√π的取值范围确定m的取值范围即可．

【解答】∵表示无理数√π的点在A、B两个点之间，

∴2＜√π＜3，∴4＜m＜9，∴10不在以上范围内，故选：A．

【点评】本题考化成了实数与数轴及无理数的知识，解题的关键是根据无理数的取值范围确定有理数m的取值范围

考点5 实数大小比较

【点评】此题考查了实数的大小比较，关键是利用平方根的定义得到3即为√9解答．

考点6 实数的运算

6．（2018秋•丰台区期末）右图是一个无理数筛选器的工作流程图．

（1）当x为16时，y值为 ______；

（2）是否存在输入有意义的x值后，却始终输不出y值？如果存在，写出所有满足要求的x值；如果不存在，请说明理由；

（3）如果输入x值后，筛选器的屏幕显示"该操作无法运行"，请你分析输入的x值可能是什么情况；

（4）当输出的y值是√3时，判断输入的x值是否唯一，如果不唯一，请写出其中的两个．

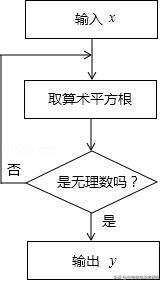
【解答】（1）当x＝16时，√16＝4，√4＝2，则y＝√2；

故答案是：√2．

（2）当x＝0，1时，始终输不出y值．因为0，1的算术平方根是0，1，一定是有理数；

（3）当x＜0时，导致开平方运算无法进行；

（4）x的值不唯一．x＝3或x＝9．

五．专题练习

需要详细的word版的专题练习可私信留言索取。

,