求由下列曲线围成的图形面积（化曲为直重新理解有曲线围成的图形的面积计算方法）

“化曲为直"的思想是数学思维的很重要的思想，它小到简单的图形计算，大到微积分的解题，无不渗透了这种数学思想。

下面就小学数学与圆（弧）相关面积计算问题，用“化曲为直”的思想重新理解，你会感到非常有意思。

例一:圆的面积计算:S=πr^2。

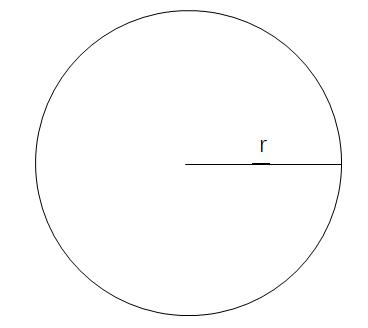
把圆看作底为圆的周长C、高为r的三角形。

三角形的面积=底×高÷2=C×r÷2

=2πr×r÷2=πr^2=圆的面积

例2:把扇形看作底为弧长、高为扇形半径r的三角形。

设扇形圆心角为n度，则弧长:

I=n/360×2πr=n/180×πr

S△=底×高÷2=|×r÷2=n/180×πr×r÷2

=n/360×πr^2

例三、把圆环、扇环看作梯形，自己算一算，试一试？

数学就是这么有意思，你换一个思路去思考一下，展现在你面前的就是全新的思维境界。