t检验的基本思想（印象流骗了你多久）

大家好，我是长歌，非常开心来到临床研究的板块，未来我将从小白的角度，尽我所能用通俗易懂的语言与大家一起重温那些统计学习中的“爱恨情仇”。

“二战”期间，为了加强对战机的防护，英美军方调查了作战后幸存飞机上弹痕的分布，决定哪里弹痕多就加强哪里。

然而统计学家沃德力排众议，指出更应该注意弹痕少的部位，因为这些部位受到重创的战机，很难有机会返航，而这部分数据被忽略了。事实证明，沃德是正确的。

这是一段来自2018年高考全国II卷的作文材料，也是当下被人所津津乐道的“幸存者偏差”的常用举例。

作为一名科研人，应当如何用理性思维战胜直觉思维，如何抽丝剥茧，透过现象观察本质呢?今天我们就由这个例子，从统计学角度探讨一下故事背后的深层含义。

首先，我们设想一下为什么军方与沃德的意见并不一致？军方观察到的是：机翼弹痕多，机尾弹痕少，自然而然地联想到：应当加强弹痕多的位置，因为更容易被子弹射击，这是基于“机翼弹痕多”的事实观察。

那么好的，我们先把以上问题简化为一个统计学问题：这场战争中飞机的机翼与机尾哪儿的弹痕更多？

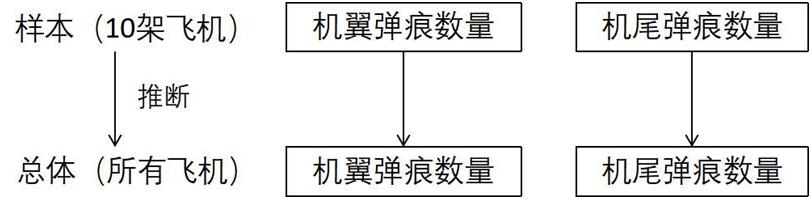
那么在这个问题中，幸运飞回基地的10架飞机是我们观察的对象，也就是样本，而这场战争中的所有飞机是我们的总体，咱们现在要做的事情是，观察10架飞机上机翼与机尾的弹痕推断整场战争中所有飞机机翼与机尾的弹痕情况，做的是一个由样本推断总体的计算。

由上图，我们肉眼可见地对比出机翼弹痕的数量显然较机尾更多，那么，我们是否就可以得出相同的结论了呢？别着急！还没到时候~

我们先来捋捋，既然我们要对比机翼和机尾上的弹痕数量，而且还要从样本推断总体，那么先自我提问一下：这10架飞机机翼和机尾上的弹痕数量，能代表真实情况下所有飞机的弹痕情况吗？

这个问题是否定的，也就是军方所犯错误的来源：这10架飞机并不能代表战争中飞机受伤的情况，因为很大一部分被击落的飞机已经无法统计了，并且机尾受伤的飞机，很大概率已无法安全返航。

这个例子讲到这里，问题也变得明朗了起来，我们至少明白，如果要做统计推断，抽取的样本要能够代表总体真实的分布情况。

实际上，我们在论文中进行的组间差异的比较，都是通过样本来推断总体情况的。我们常见的组间比较的方式包括t检验、卡方检验、致和检验等等，每种方法的“使用条件”都不一样。

我们说，医生使用统计方法，应该和“看病抓药”一样，要先对数据“望闻问切”，然后再对症下药，选择适合的统计方法。下面就跟随长歌老师来逐个熟悉这些检验方法的“适应症”和具体操作流程吧。

今天我们先来介绍应用最广泛的“独立样本t检验”，它的主要应用条件是①独立性、②正态性、③方差齐性的条件，那这又是什么意思呢？

这里我们重新引入一个新例子：现有一治疗新冠肺炎药物，各有20例治疗组与20例未治疗组病人，我们想要比较治疗后其病毒载量（IU/mL）是否相同?

这时候首先需要理清楚我们的研究目的，我们要比较的结局Y变量是“病毒载量”，是连续变量；而分组因素是“是否治疗”，因此这属于“两样本间连续资料的差异检验”。

根据上图,我们应首先考虑其是否满足独立样本t检验的使用条件。

（1）独立性：独立性强调的是观测的数据之间是否独立。在这个例子中，病毒载量为一连续型资料，我们一般认为每例病人的病毒载量是与其他病人无关的，是不会互相影响的，因此是相互独立的事件。

最常见的数据不独立的形式是：同一个病人连续两天测得的病毒载量，那么这两天的病毒载量数值是来自同一个人的，因此后一天的载量与前一天是有关系的，我们一般认为这两个数据不是独立的。

因此数据独立性是通过“主观判断”的，不需要借助统计软件来“验证”。数据不独立的情况我们只要记得这种特殊的案例即可，我们未来会专门讨论数据不独立的时候的分析方法。

（2）正态性：为何两个独立样本比较还需要满足正态性呢？因为t检验本质上是对两组样本的均值进行的比较，从而推断的总体差异，而非正态性的资料并不适合用均值进行描述。

来举一个例子，我手头有20例病例，我需要用这20例病例（样本）去推断真实的总体情况，那么，我所抽样的这些样本要符合总体分布的情况，才能去比较治疗组和非治疗组的差别。

例如下图，蓝色曲线为一正态分布资料，我们假设它为治疗组的病毒载量情况，而红色曲线为一偏态分布资料，我们假设其为未治疗组的病毒载量情况，由图可见，似乎两组的均值是接近甚至一样的，没有差异，但事实结论确实如此吗？

理性一些，未治疗组的抽样样本分布并未服从正态或者近似正态分布，也就是说，未治疗组的这20个病例，包括其均数、标准差等并不能很好地描述真实情况下总体的情况。

因此这时候直接比较两组，发现均值一样就认为两组总体参数一致，实际上是错误的。

再举一个形象的例子：一个工资正态分布的企业A和工资偏态分布的企业B（老板工资很高，员工工资很低），这会儿我作为应聘者，想比较两个公司普通员工的工资情况，应该看什么参数呢？

上面我们说到，t检验的本质是比较两者间的均值，如果我们作为当事人，乍看之下以为两者的平均工资是一样的，但从上帝视角来看，两者显然不一样，老板过高的工资造成了员工平均工资都很高的假象。

因为你入职以后肯定不会是“老板”，所以到B企业的话你拿到的工资很有可能低于平均值。

因此，进行两组独立样本的比较前需要检查数据是否为正态分布。

正态性检验常用的方法有Kolmogorov-Smirnov检验（KS检验）和Shapiro-Wilk检验（SW检验），当检验结果的p值小于0.05，则认为数据不满足正态性（这里我们姑且将这个结论记住）。

通过上面的思维导图我们知道，当数据不满足正态性的时候，我们就不能使用独立样t检验了，需要考虑使用秩和检验来进行组间差异比较。这个我们下一期再说。

（3）方差齐性：同样地，为啥我们作两组间均数的比较还要满足方差齐性？

抛给大家一个问题，奥运会为啥举重要分不同公斤级？这因为一个人能举起的重量与本身的体重是有一定关系的，要不然100kg级的选手岂不是随意去虐菜75kg级的选手了！

两组独立样本的比较同样如此，我们需要确保两组数据来自同一整体，说人话，也就是“同质性”。

如同下图我们可见，蓝色曲线为一“高耸”曲线而红色为一“扁平”曲线，两组曲线均满足正态分布，“扁平”曲线和与一“高耸”曲线的均值可能相同，但其整体是肉眼可见的不同。因此如果我们只关心均值，会认为两条曲线来自同一总体，显然这里做出了假阴性结论。

因为虽然两条曲线的平均水平相差不多，但真实情况显然不同的。对于方差齐性检验，我们常采用Levene’s检验，同样也是当检验的结果P >0.05时，才可以认为两组方差齐。

当两组方差不齐的时候，我们可以考虑使用校正t检验，也就是在原来的t检验基础上进行相应的“调整”。

说了这么多原理，相信小伙伴们有点云里雾里了。

没关系，我们只需要记住我们t检验的适应条件是：两组样本间连续样本的均值比较；使用条件是独立、正态和方差齐即可。而正态性、方差齐性以及t检验本身，都是可以通过软件实现的。

下面我们来具体学习一下如何通过软件操作或者上面这些信息吧。

下图展示的是治疗组（分组：1）与未治疗组（分组：2）的病毒载量水平（部分数据）。大家一定要记住我们的数据呈现方式，即：每一行代表一个个体，每一列代表的是同一个变量。

首先我们对两组数据进行正态性检验，我们需要点击的按钮是：“数据”→“探索”→“图”勾选“含检验的正态图”。

输出框后可得结果K-S检验与S-W检验均未小于0.05，故其数据满足正态分布。如两者均小于0.05，那我们就该重新回到思维导图的起点，寻找秩和检验的解决方法了。

做完正态性检验，是否需要立马进行方差齐性检验呢？大家应该可以感觉到，方差齐性检验并不是“非常重要”，因为它不满足的时候，只要对t检验结果进行“微调”变成校正t检验即可。

因此，基于这个思想，SPSS也是直接将t检验和校正t检验的结果一同输出，供我们选用。

在“分析”→“比较平均值”→“独立样本t检验”中，按照相应内容填入；如图，此时的“检验变量”指的是“病毒载量”，而分组变量指的是“是否治疗组”，这些应该都非常好理解。

最后点击确定，输出结果，显示治疗组的病毒载量均值为116.15，标准差为51.809；未治疗组病毒载量351.65，标准差为90.285。

Levene’s检验结果显示，F=2.629，P=0.113，P>0.05提示两组数据方差齐，因此可以采取两独立样本t检验的结果（也就是第一行的结果），如果方差不齐，应当采取校正t检验，即第二行的结果。

在t检验中，最重要需要报告的一个统计量是t值（本例为-10.118）和P值（本例为P<0.001）。

我们得出结论：接受该新冠药物治疗组与未接受此种治疗组病毒载量水平存在统计学差异，未治疗组平均病毒载量水平高于治疗组。

最后，我们再重新回顾一下今天的主角：独立样本t检验

应用场景：检验连续性变量在两组间均值是否有差异；

应用条件：满足样本的独立性、正态性及方差齐性；

当不满足方差齐性时，采用校正t检验。

但是，现实场景中，我们时常会遇到不是正态分布的资料要进行组间比较的情况，聪明的你一定从思维脑图中得到的答案了，可以进行“秩和检验”。秩和检验是怎么回事呢？我们下期进行详解。

,