如何快速记住数学的基本不等式（高观点下的初等数学）

莱布尼兹级数是数学中常见的一个级数，这个级数最显著的特点就是分母都是奇数，分子都是1，他首次有数学家莱布尼兹给出，这是一个伟大的发现。本篇我们就从初等数学原理出发来证明这个伟大的发现。

前面的相关的文章，我们已经知道用sinx根式的线性因式的无穷乘积来表示sinX，我们在此引入自然对数的形式，这个对数将彻底改变sinx无穷乘积的线性因式

根据对数的基本原理，上式的乘积形式就变成了对数形式下的加法运算，如下

我们将上式两边求导，左边等式就等于cosx/sinx，那么右边的等式求导就得到

求导后，右边等式第一个项和第二项就变成了如下的样式

右边第三项求导就是1/(π X)

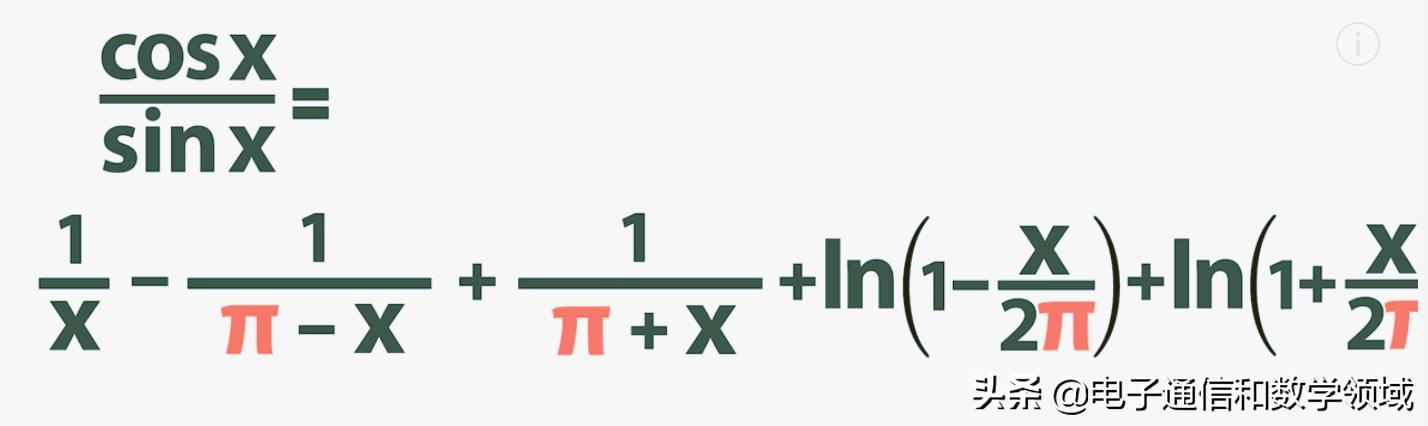
最终我们得到等式左边和右边求导后的所有样式

我们让X=π/4，就得到

整理上式得到

所以等式左边等于1

最终我们得到莱布尼兹的级数形式