数字信号的方差（信号处理中的平均偏差）

本文从信号处理应用的角度讨论了三种统计性描述方法。

在上一篇有关电气工程师的统计性描述的文章中，我们看到均值和中位数都可以传达数据集的集中趋势。尽管中位数对异常值的敏感度较低，但在电子和数字信号处理中更经常使用均值。实际上，算术平均值是电气工程中必不可少的统计技术。

但是，我们通常不仅仅需要一种手段来充分描述或理解数据集。

当我们仅报告中心趋势时，我们没有考虑数据的重要方面，即值偏离中心趋势的方式。

偏离均值

假设我们已经数字化了两个模拟输入信号。如果我们将数字代码转换回伏特单位并绘制离散时间波形，则它们看起来像这样：

我们可以通过查看曲线图来很好地猜测均值：蓝色信号的中心趋势是1.2 V，红色信号的中心趋势是0.8V。但是，如果我们仅报告均值，我们将给人的印象是，这两个信号之间唯一重要的差异是平均值的0.4 V差异（或者我们可以将其称为DC电平或DC偏移）。显然，这个故事还有更多。

电气工程师会本能地将这些波形识别为稳定的DC信号（也许是电源电压），其中包括相当多的噪声。更重要的是，我们立即意识到，蓝色信号比红色信号噪声大。如果仅考虑平均值，则将丢失噪声性能的主要差异。顺便说一下，为什么我们会在这些信号中感知到噪声？因为各个值明显偏离平均值，他们这样做的方式似乎是随机的，并且相对于平均值，偏差很小。

当统计学家看到均值小的随机偏差时，电气工程师会看到噪声。

平均偏差

这些信号有多吵？有点吵？非常吵闹？让我们尝试为该问题提供更精确的答案。换句话说，我们需要量化这些数据集中的偏差。

量化偏差时，我的第一个直觉是找到每个数据点与平均值之间的距离，然后计算所有这些距离的平均值。这将为您提供平均偏差（也称为平均绝对偏差），即，值偏离中心趋势的典型量。这是数学语言中的平均偏差：

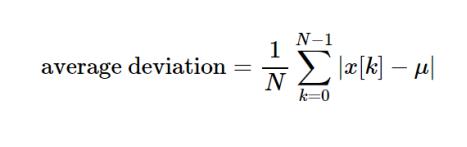
其中N是数据集中值的数量，μ是平均值，x [k]是表示为离散时间变量k的函数的信号。

在该曲线图中，水平线表示电压水平，该电压水平是平均值之上和之下的一个平均偏差。

尽管平均偏差是直观的，但它并不是量化信号偏离均值趋势的最常用方法。为此，我们需要标准偏差。

方差和标准偏差

在电气工程中，平均偏差的问题在于我们正在平均电压（或电流）差，因此我们在幅度范围内进行操作。噪声现象的本质是，在分析噪声时，我们强调幅度上的功率，因此，我们需要一种在功率范围内运行的统计技术。

幸运的是，这很容易实现。功率与电压或电流的平方成正比，因此，我们要做的就是在求和和求平均值之前将差项平方。这个过程导致称为统计度量方差，由σ2表示（发音为“西格马平方”）：

我们可以将方差描述为表示为功率的信号随机偏差的平均功率。这意味着方差与我们开始使用的值没有相同的单位。如果我们正在分析电压信号的波动，则方差的单位为σ2而不是σ。

如果要表达信号使用原始单位随机偏离的趋势，则必须通过将平方根应用于最终值来补偿平方差：

该过程生成称为标准偏差的统计量度，即，信号随机偏差的平均功率表示为幅度。因此，如果我们正在分析电压信号，则尽管我们使用电压偏差的平方来计算标准偏差，但标准偏差的单位为σ。

在该图中，水平线表示电压水平，该电压水平是平均值之上和之下的一个标准偏差。

方差和标准偏差以不同的方式表示相同的信息。尽管据我所知，方差在某些分析情况下更为方便，但通常最好选择标准差，因为它可以直接解释为衡量信号偏离均值趋势的度量。

结论

标准差和方差是在科学和社会科学中经常出现的基本统计技术。我希望本文能帮助您理解这些概念与电信号之间的基本联系，并且在下一篇文章中，我们将介绍一些与标准偏差有关的有趣细节。