十秒带你记住三角函数（极客数学帮三角函数知识点总结）

三角函数是初中开始接触的一个至关重要的知识点，高中开始这个知识点的难度会逐渐加深。那么今天极客数学帮就来和大家一起看看关于三角函数的知识点。

三角函数是六类基本初等函数之一，是以角度（数学上最常用弧度制，下同）为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。也可以等价地用与单位圆有关的各种线段的长度来定义。三角函数在研究三角形和圆等几何形状的性质时有重要作用，也是研究周期性现象的基础数学工具。

1、勾股定理：直角三角形两直角边a、b的平方和等于斜边c的平方：a2b2=c2

2、如下图，在Rt△ABC中，∠C为直角，则∠A的锐角三角函数为(∠A可换成∠B)：

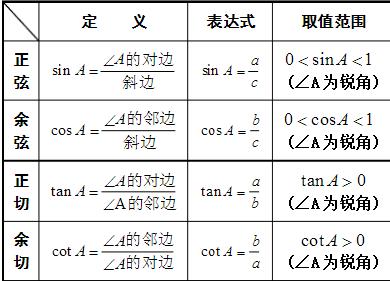
3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。

4、0°、30°、45°、60°、90°特殊角的三角函数值(重要)

三角函数	30°	45°	60°
Sinα	1/2	（√2）/2	（√3）/2
Cosα	（√3）/2	（√2）/2	1/2
Tanα	（√3）/3	1	√3

直角三角形三角函数定义

在直角三角形中

当平面上的三点A、B、C的连线，AB、AC、BC，构成一个直角三角形，其中∠ACB为直角。对∠BAC而言，对边a=BC、斜边c=AB、邻边b=AC，则存在以下关系：

基本函数	缩写	表达式	语言描述
正弦函数	Sin	a/c	∠A的对边比斜边
余弦函数	Cos	b/c	∠A的邻边比斜边
正切函数	Tan	a/b	∠A的对边比邻边
余切函数	Cot	b/a	∠A的邻边比对边
正割函数	Sec	c/b	∠A的斜边比邻边
余割函数	Csc	c/a	∠A的斜边比对边

解直角三角形的定义：

已知边和角（两个，其中必有一边）→所有未知的边和角。

依据：

①边的关系：a2b2=c2

②角的关系：A B=90°；

③边角关系：三角函数的定义。(注意：尽量避免使用中间数据和除法)

任意角三角函数定义：

在平面直角坐标系xOy中设∠β的始边为x轴的正半轴，设点P（x，y）为∠β的终边上不与原点O重合的任意一点，设r=OP，令∠β=∠α，则：

了解了有关于三角函数的知识点，根据自己掌握的情况来做做下面的练习题吧。

精心选一选

1.在直角三角形中，各边都扩大2倍，则锐角A的正弦值与余弦值都（ ）

A、缩小2倍 B、扩大2倍 C、不变 D、不能确定

2.在Rt△ABC中，∠C=90° ，BC=4，sinA=4/5，则AC=（ ）

A、3 B、4 C、5 D、6

3.若∠A是锐角，且sinA=1/3 ，则（ ）

A、00<∠A<300 B、300<∠A<450 C、450<∠A<600 D、600<∠A<900

4.若cosA=1/3，则(3sinA-tanA)/(4sinA 2tanA)=（ ）

A、0°<∠A<30° B、0°<∠A<45° C、0°<∠A<60° D、0°<∠A<90°

5.在△ABC中，∠A：∠B：∠C=1：1：2，则a：b：c=（ ）

A、1：1：2 B、1：1：2 C、1：1：3 D、1：1：22

6.在Rt△ABC中，∠C=900，则下列式子成立的是（ ）

A、sinA=sinB B、sinA=cosB C、tanA=tanB D、cosA=tanB

7.已知Rt△ABC中，∠C=90°，AC=2，BC=3，则下列各式中，正确的是（ ）

A.sinB=23 B．cosB=23 C．tanB=23 D．tanB=3 2

8.每周一学校都要举行庄严的升国旗仪式，让我们感受到了国旗的神圣．某同学站在离旗杆12米远的地方，当国旗升起到旗杆顶时，他测得视线的仰角为30°，若这位同学的目高1.6米，则旗杆的高度约为（ ）

A．6.9米 B．8.5米 C．10.3米 D．12.0米

细心填一填

1、在Rt△ABC中，∠C=90°，AB=5，AC=3，则sinB=_____．

2、在△ABC中，若BC=2，AB=7，AC=3，则cosA=________．

3、在△ABC中，AB= ，AC=2，∠B=30°，则∠BAC的度数是______．

4、求值：sin260° cos260°=___________．

5、在直角三角形ABC中，∠A=90°，BC=13，AB=12，则tanB=_________．

参考答案

一：1、C 2、A 3、A 4、D 5、B 6、B 7、C 8、B

二：1、3/5 2、√7/2 3、.30°4、.1 5、5/12

,