想象不出克莱因瓶的样子（我们能造出莫比乌斯环）

现实生活当中，经常有人会将人类和蚂蚁做对比，甚至认为蚂蚁属于一种二维生物。这是因为蚂蚁的视力很弱，基本是依靠气味和触觉判断方位的，所以蚂蚁眼中的世界是二维的，由简单的点和线构成。但是我们看到的蚂蚁明显是三维的，起码它们并不是一张纸。针对这类疑惑，科学家们试图使用几何让我们理解各个维度之间的区别，因此特殊的模型出现了，它们就是莫比乌斯环和克莱因瓶。

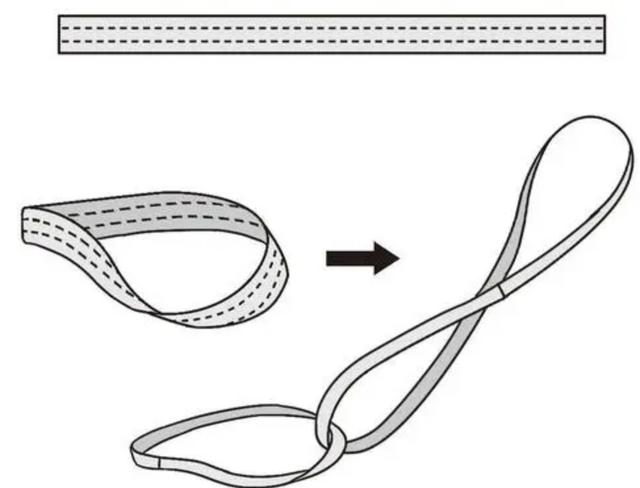
对于莫比乌斯环，大家肯定都不陌生，毕竟这几年“莫比乌斯环状戒指”算得上是热卖的首饰之一，人们认为它能代表永恒、无限的爱情。它的制作方法很简单，我们对一张A4纸进行裁剪，剪出一张细长的纸条，将它两头抓住扭转180°，再粘在一起，一个简易的莫比乌斯环就做好了。可是另一个模型克莱因瓶，却无法被造出，只能存在于电脑程序建模当中，这又是为什么呢？原来是因为它并不属于我们这个三维世界，而是来源于更高的四维空间。

探究莫比乌斯环和克莱因瓶的奥秘之前，我们需要先了解一下它们的来源。其实最初它们都源于数学当中的几何学，现在已经变成了几何学的重要分支，改头换面取了个新名字叫做“拓扑学”。

这门学科最早发展于19世纪，起源则要往前追溯一些，具体可以到18世纪。主要用于研究几何模型或者空间学的，特殊之处在于拓扑图形的性质，就是不论你如何将它弯曲、缩小或者变形它都能保持不变，因此还得了一个别称叫“橡皮几何学”。

拓扑学研究的图形会使人感到十分费解，人们不能理解为什么要研究这些奇怪的图形。这里要解释一下，在我们的惯性思维当中，一切看到的图形都是在欧几里得几何定义之下的，是一种合乎“正常”的模样。

但是拓扑学则最大程度地跳出了这一定义，几何图形或者模型在这里有着更大的自由度，因此它们看起来奇形怪状的甚至说更加的抽象，与我们看到的欧几里得几何定义下的世界完全不同。因此可以说拓扑学是属于纯粹思维逻辑领域的学说，大家就不要以惯性的思维去看待这些图形有没有意义，这是一个思维误区。

综合拓扑学的发展以及相关定义来看，这门学科其实更像是一种思维游戏，绝大多数时间需要依靠大家自行发挥想象力，如果你只是用惯性思维进行看待，那么确实就是一个非常无厘头的几何模型。但是如果大家闭上眼睛进行想象，会发现它不同于传统数学，有精准的数字或者概念规定，因此拓扑学在现实中的应用其实很少，它更多时候发生在思维层面当中。

下文当中要介绍的莫比乌斯环和克莱因瓶就是拓扑学的典型研究对象，所以希望大家在观察这两个图形的时候，跳脱出直观世界的限制，不要将重点放在争论它到底有没有意义，或者合不合理。

莫比乌斯环也可以叫莫比乌斯带，它是1858年由德国数学家莫比乌斯和约翰·李斯丁共同发现的。它不同于普通纸带有两个面，它只有一个面，其边界由一条闭合曲线组成。假如将一只蚂蚁放在普通的纸条上，蚂蚁想到达另一面，肯定需要跨越纸面的“边界”，但是在莫比乌斯环之上“边界”神奇地消失了，蚂蚁可以不用跨越任何边缘地带就抵达另一面，甚至是回到起点。

莫比乌斯环的制作比较简单，所以这些年来常常出现在大众视野当中。但是细分之下它还能分为两种不同的类型，这是由大家扭转纸带的方向决定的，向左扭动则得到左旋莫比乌斯环，向右则得到右旋的，不知道商家在制作戒指时会不会注意到这一特点，可以以此来区分男戒和女戒，毕竟刚好与男左女右对应了。

很多人会觉得不就是简单地扭动了一下，说白了它还是个纸条而已，那么我们不如来看看莫比乌斯环和普通环圈之间的区别。首先，我们先使用裁剪的方式，看看它们会有什么不同。将普通纸环沿着中线剪开，那么你就会得到一个与原来纸环周长相等但是宽度更窄的环。但是如果是将莫比乌斯环沿着线剪开，你得到的纸环周长是原来纸环的一倍，大家有兴趣可以剪来试试看。

如果在莫比乌斯圈上划上两条等距离线再进行剪裁，那么你不仅能得到一个比原圈周长长一倍、比原圈宽度窄三分之二的普通环圈，同时还能在其中心部位再得到一个单独的、比原圈宽度窄三分之二，且周长与原圈等长的“窄”莫比乌斯圈。

可能会有人疑惑这种剪纸实验确实能证明它与普通的环圈不同，可是除此之外还有什么用呢？通过上述的裁剪结果可以看出，我们在三维世界当中对它剪裁，竟然是无法将它还原的，而是会剪出新的样子，这一部分呈现出的是“非三维”的状态，我们通过外力也无法将其改变。因此可以得出莫比乌斯环实际上是一种非三维的物体，我们能够将它制作出来完全是因为在这之上套上了两个三维坐标系。

充分了解了莫比乌斯环之后，我们就可以来看看它的升级版“克莱因瓶”了。为什么这么说呢，因为数学家已经证明了这两种模型之间是有联系的，在我国数学专家谈祥柏先生的著作《数学广角镜》当中就明确指出其实克莱因瓶是由两个莫比乌斯环组合而成的。

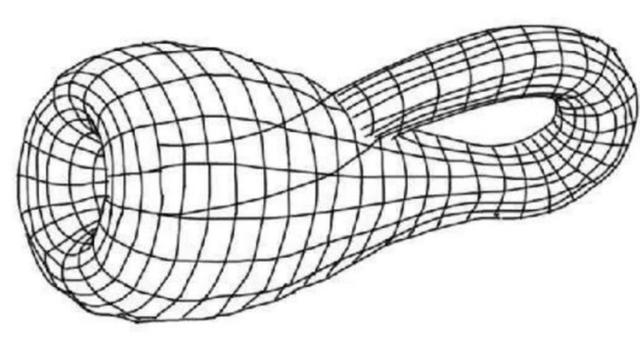
克莱因瓶是数学家菲利克斯·克莱因在1882年时发现的，对比上文莫比乌斯环的诞生时间，克莱因瓶要更年轻一些。这个瓶子同样也没有边界，整个表面都是封闭的曲面。大家可能不好想象封闭曲面，其实球体上的曲面就是封闭曲面，假如有人问你地球有边界吗？你一定会很纠结，感觉上是有的，但是以球面来说是没有的。这类无定向性的平面，并没有内部和外部的区别。

这个瓶子看起来没有瓶底，瓶颈则被拉长了，看起来是穿过了瓶壁与瓶底连接在了一起，但是如果在电脑建模当中它是没有穿过的。假如我们将莫比乌斯环上的蚂蚁放在克莱因瓶上，那么它能够穿过瓶颈，由瓶子的外部爬到瓶子的里面。不过我们都知道克莱因瓶不分里外，这种比喻只是便于大家理解。

目前市面上一些商家出售的克莱因瓶，都能明显地看到瓶颈伸入了瓶壁才到达底部。因此按照克莱因瓶的定义来说，这些都是虚假制品，真正的克莱因瓶是无法被制造的，这又是为什么呢？

先来看看能被制造出的莫比乌斯环的性质，前文提到了它属于非三维的物体，但是用来制作它的纸条本质上是属于二维的。大家小时候看的动画片大部分也是二维的，那上面的人物就像纸片一样单薄，因此我们也叫它们“纸片人”。所以莫比乌斯环其实是使用二维变换，证明了三维的一些理论。

可是克莱因瓶本质上已经属于四维空间了，因此我们在三维空间当中制作出的克莱因瓶看起来不伦不类，完全与它的本质不符。克莱因瓶连续性的特质正是导致它无法被制成的根本原因，实际制作当中，这个瓶颈与瓶壁的面势必会产生相交，导致连续性发生中断。所以我们看到的商家出售的那些克莱因瓶，早已失去了连续性和单侧性，这种瓶子完全不符合克莱因瓶的理论。

所以，三维世界中瓶颈和瓶壁相交的那个点，是它们在三维坐标系当中共用了一个位置，如果放进四维空间，就不会有相交的表现。大家可以试着想象将那个位置提起来，绕过瓶壁。就像最初数学家们为了方便我们利用线条理解莫比乌斯环举的例子，如果在纸上画一个8，那么它中间的位置必然是相交的。

但是使用拓扑学，用一个橡皮圈绕着一个8的形状，那一位置就没有相交，你可以轻松地拿起位于上端的部分。莫比乌斯环从简单的二维跨越到了三维，正是利用这种方法。

虽然莫比乌斯环本质上也不是三维物体，但是起码它有一部分是属于三维的，因此我们能够按照其定义将模型制作出来。真正的克莱因瓶需要放置在四维空间当中，才能体现出连续性闭合曲面的特质。

人类的想象力其实已经十分丰富了，我们从来不拘于如今的所见所想，因此我们才一直寻找外星的生命，探寻多维的宇宙。多维是否存在的问题爱因斯坦在一个世纪前的相对论当中就像我们提出了，“物质告诉时空如何弯曲，时空告诉物质如何运动”，在这一理论当中时间和空间是交叉的，并不是传统意义上的平行线。如果大家有兴趣，可以去了解一下广义相对论当中所描述的弯曲的时空，一定会因此打开新世界的大门。

诚然，多维度空间一定是存在的，不过其模样实在是超乎了我们的认知范围，这就类似于蚂蚁看人类活动，它们完全不能理解我们修建的高楼大厦到底是什么，而人类对于高维空间的理解也很难跳脱出现有思维的限制。我们在看拓扑模型时都感觉晕头转向，更不用说描述高维度空间了。

《三体》的结局当中，宇宙中的歌者文明向太阳系扔了一片二向箔，便轻松地把我们本是三维立体的太阳系变成了二维图片，直接把其中的所有球体按压成了一张纸，这就是所谓的降维打击。

所以我们无法制造出克莱因瓶的原因，其实和降维打击有些类似，大概就是四维空间对三维空间的限制吧！如果我们无法具象建成四维空间的模型，去形象理解四维空间，那么克莱因瓶在我们眼中永远都是一个长相奇怪的“瓶子”。