最新高中数学函数的解题方法（高中数学函数多选题）

下列说法，正确的有( ).

A. 函数f(x)=lnx 3x-6 的零点只有一个且属于区间(1,2).

B. 若关于x的不等式ax^2 2ax 1>0恒成立, 则a∈(0,1).

C. 函数y=x的图像与函数y=sinx的图像有3个不同的交点.

D. 函数y=sinxcosx sinx cosx, x∈[0, π/4]的最小值是1.

我们逐个选项分析。一般老黄都比较强调有图有真相，A选项作出大概图像，立马可以解决。

上图中y=lnx和y=-3x 6两个函数图像的交点就表示原函数的零点。一个函数的零点可以表示为两个函数的差等于0的情形。从图中一目了然可以看出两个图像有唯一的交点，且在(1,2)之间。

或者可以求原函数的导数，f’=1/x 3, 在函数的定义域x>0上，f’>0, 所以f是严格递增函数，这说明函数最多只有一个零点. 如果不会用导数证明函数的增减性，也可以用下面的一般方法：

设0<x1<x2,

则f(x2)-f(x1)=ln(x2/x1) 3(x2-x1)>0, 所以f是严格递增函数.

然后分别求得f(1)=-3<0, f(2)=ln2>0, 根据根的存在性定理就可以知道, f唯一的零点在(1,2)上. 因此A选项是正确的.

B选项也可以借助图像来理解一下。

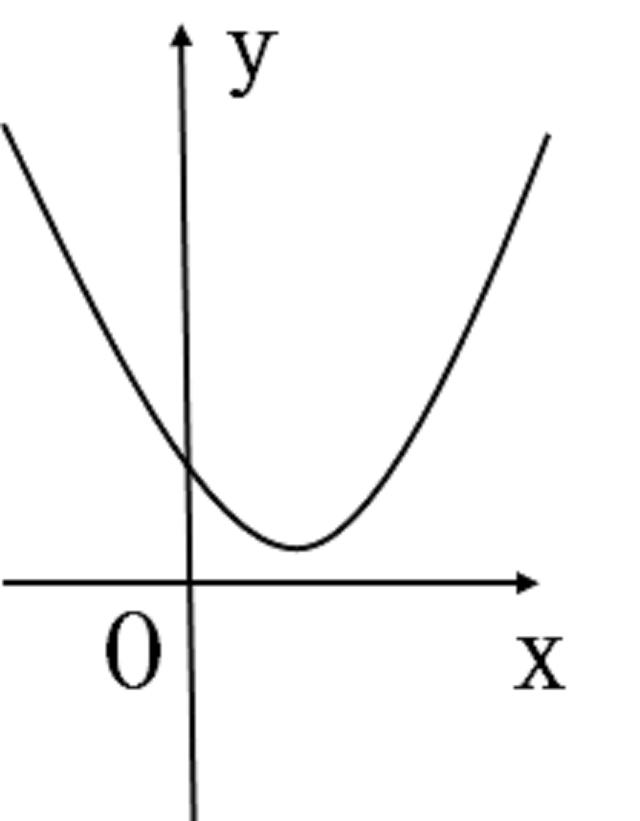
可以看到，要使不等式恒成立，有两个必要条件，一是a>0，二是判别式△=4a^2-4a<0.

可以解得0<a<1, 即a∈(0,1). 所以B选项也是正确的。

这里存在争议，当a=0时，不等式是成立的，但却不是关于x的不等式。所以这样的题最好少出。

C选项也借助图像大概了解一下：

可以看到，单凭图像无法做出准确的判断。最好是通过求两个函数的差构成的新函数的导数，通过判断新函数的增减性来确定。

记f(x)=sinx-x, 则f’(x)=cosx-1≤0,

即f是增函数, 增函数要么只有1个零点，要么有无限个零点. 因此C选项是错误的。如果不会用导数判断就麻烦了一些。我们可以发现图像是关于原点对称的，所以我们可以分开正负区间分析。比如在(0,π/2)的区间上分析。

设0<x1<x2<π/2,则0<(x2-x1)/2<(x2 x1)/2<π/2,

sinx2-sinx1=2cos[(x2 x1)/2]sin[(x2-x1)/2]<2cos[(x2-x1)/2]sin[(x2-x1)/2]=sin(x2-x1),

又sin(x2-x1)<x2-x1,

∴f(x2)-f(x1)=(sinx2-sinx1)-(x2-x1)<sin(x2-x1)-(x2-x1)<0.

同理可证-π/2<x1<x2<0的情形.

以上证明了f在(-π/2,0)和(0,π/2)上都严格单调增，因此至多在x=0有一个交点。而当|x|>π/2时，两个函数不可能有交点，从而可以知道C选项是错误的。

D选项并不容易作图像，所以直接在函数上做文章。可将函数化为y=sin2x/2 根号(1 sin2x), 利用换元法，记u=sin2x ，则u∈[0, 1], y=u/2 根号(1 u). 很明显，这是一个单调增函数。而在x∈[0, π/4]，u=sin2x也是单调增的。从而可知当x=0时, u=0, y=1最小。所以D选项是正确的。

综上，正确的答案是ABD. 错选，多选都不得分，少选要扣分。