构造数列的公式（图解普林斯顿微积分读本）

第 22 章 数列和级数：基本概念 (Sequences and Series: Basic Concepts)

本章的内容：

• 数列的收敛和发散;

• 两个重要数列;

• 数列极限和函数极限之间的联系;

• 级数的收敛与发散, 以及几何级数的敛散性讨论;

• 级数的第n 项判别法;

• 级数和反常积分的联系;

22.1 数列的收敛和发散(Convergence and Divergence of Sequences)

数列是一列有序的数, 可能是有限项, 也可能有无穷项, 其中有无穷项的数列叫作无穷数列(infinite sequence).

下角标经常用于数列中, 其中 a1 表示数列中的第一项, a2 表示第二项... , 数列经常由一个公式来给出, 比如:

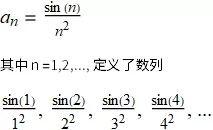
对于无穷数列, 我们主要讨论当 n 趋于无穷时数列的极限值. 数学上表示为, 极限:

是否存在. 如果存在, 值是多少. 如果越来越趋近于L 并一直保持这种趋势. 则数列 an 收敛, 否则发散.

22.1.1 数列和函数的联系

在水平渐近线上, 数列和函数有类似极限性质:

另一个重要的事实是三明治定理, 即夹逼定理, 对数列也适用. 此外连续函数保持极限以及洛必达法则对于数学都适用.

22.1 .2 两个重要数列

取常数 r, 考虑从 n=0 开始取值的数列 an=r^n , 这是一个等比数列:

上面这些都是下述一般规则的特例:

另一个很有用的数列, k 为任意常数:

22.2 级数的收敛与发散

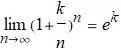
级数(Series)就是将数列 an 的所有项都相加起来. 无穷级数可写为:

重要的一点是：级数收敛还是发散与起始项无关!

几何级数(理论) Geometric series

来看如下一个等比数列的无穷几何级数的重要例子, 问题是, 该级数收敛吗？若收敛, 收敛于何值？

为了求解, 我们最好看一下部分和. 选择数 N, 则部分和 AN , 用求和号表示为:

22.3 第n 项判别法(理论)

但注意: 第n 项判别法不能用于级数收敛性的判别!

22.4 无穷级数和反常积分的性质

反常积分的四个判别法对无穷级数仍适用.

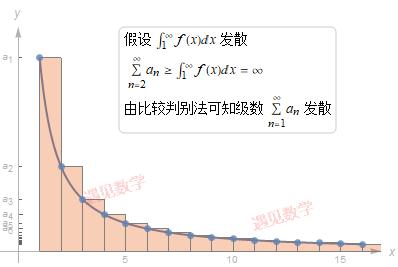
22.4.1 比较判别法(理论)

假设级数 ∑an 每一项为正, 若级数发散, 则只要找到一个更小的发散级数 ∑bn , 即证.

22.4.2 极限比较判别法(理论)

22.4.3 p 判别法(理论)

调和级数(Harmonic Series)

22.4.4 绝对收敛判别法

级数前面有限项不影响级数最终的收敛性. 所以如果级数从某一项后均为正(或者均为负), 则可只讨论后面的新级数部分.

如果是交错级数, 则用绝对收敛判别法: 若∑|an|收敛, 则 ∑an 也收敛.

22.5 级数的新判别法

22.5.1 比式判别法(理论)

该判别发只能用于级数, 级数相邻两项的比 bn . 如果新数列 bn 收敛与小于 1 的数, 则原级数收敛.

22.5.2 根式判别法(理论)

考虑的是第 n 项绝对值的 n 次方根, 构造新数列 bn=|an|^(1/n) , 求极限. 若极限<1, 则原级数收敛. 若极限值>1, 则发散. 如果极限值=1, 需要采用其他方法讨论.

22.5.3 积分判别法(理论)

(完)「予人玫瑰, 手留余香」

转发即支持, 一起来遇见数学!

,