spss 两个独立样本的秩和检验实例（SPSS数据分析之多独立样本的非参数检验操作）

多个独立样本检验，是用于检验多个独立样本之间是否具有相同的分布，零假设：多个独立样本之间的总体分布无显著性差异。

话不多说，直接上操纵。

原始数据

原始数据

问题：检验三块样地的树高是否具有显著性差异

操作：分析→非参数检验→旧对话框→K个独立样本

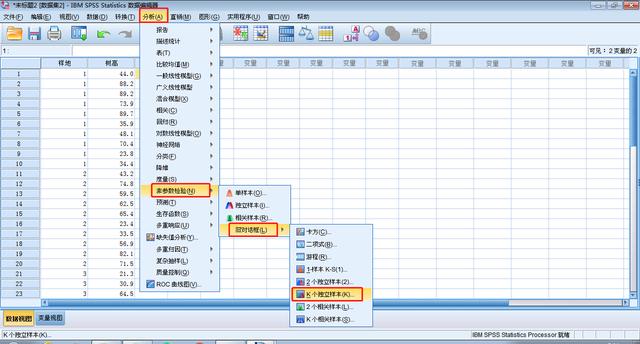
K个独立样本的操作

检验变量：树高

分组变量：样地 定义范围：最小值1，最大3

检验类型

Kruskal-Wallis H：是两独立样本的非参数检验中Mann-Whitney U的扩展，是单项方差检验分析的一个模拟，用于检验多个样本总体分布的所有差异

Jonckheere-Terpstra：在总体间进行排序的情况下，相对于其他两种检验是更适用的检验，通过计算样本中一个观测值小于另一个样本的个数来判断，比检验出现的第二类错误的概率更小，

中位数：检测位置和形状的分布差别，检验多个样本是否来自具有相同中位数的总体

选项：描述性、四分位数

检验类型

输出结果

从上表可知，树高案例个数30，均值为56.38，标准差为22。134，最小值（极小值）为21.3，最大值（极大值）为89.7。

Kruskal-Wallis 检验

上表可知，各个样地的个案数为10，均值分别为17.05/15.8/13.65，检验统计卡方值为0.763，渐近显著性为0.683＞0.05，说明这三个样地之间的树高无显著性差异。

中值检验

上表可知，各个样地大于中位数和小于中位数的个数，检验统计的渐近显著性为0.67＞0.05，说明这三个样地之间的树高无显著性差异。

上表可知，样地中的水平数（组数）为3，渐近显著性（双侧）值为0.351＞0.05，说明这三个样地之间的树高无显著性差异。

综上所述三种检验，说明三个样地之间的树高无显著性差异。

今天的数据分析就学习到这里，有任何问题可以评论留言，如有想看的操作讲解，可以私信我。谢谢大家的点赞、关注和转发。