麦克斯韦电磁学与经典力学（神奇的电磁世界）

神奇的电磁世界：电动力学(麦克斯韦方程组02)

如果喜欢的话请点点关注和转发哦，谢谢大家啦！

这个月要期末考试，因此没什么时间更新，抱歉各位。

---

介质的极化

在讨论介质中的麦克斯韦方程组之前，我们先要明白，电磁场的来源是电流和电荷，也就是说，只要空间中某处有电流和电荷的存在，那么该处就会产生电磁场。

在这一认知的帮助下，我们就可以通过寻找电磁介质中电流和电荷的总体分布来研究介质中的电磁场。

我们将一电介质放入电场中，正负电荷在外电场的作用下被拉开，形成电偶极子，这一过程就叫做极化。

电介质又存在着两种情况：

第一种电介质是在没有外电场的情况下，分子的正电中心和负电中心是重合的，没有固有的电偶极矩。当被放入电场中时，所有的正负电荷均沿着电场的方向被拉开，就会出现宏观电偶极矩的分布；

第二种电介质在没有外电场的情况下，分子的正电中心和负电中心并不重合，本身是存在固有的电偶极矩的，但是由于分子的排列是无规则的，所以在宏观上并以没有电偶极矩分布。当施加外电场后，在电场的作用下，有极分子的取向将会趋同，就会出现宏观电偶极矩的分布。

宏观电偶极矩用点极化强度矢量P来描述：

其中P_i(_i的意思是i是下标)是第i个分子的电偶极矩。

由于计划，分子的正负电中心发生相对位移，因此在ΔV内可能出现净余的正电或负电，即出现宏观的束缚电荷分布，我们现在首先要求出束缚电荷密度和电极化强度之间的关系。

设每个分子由相距l的一对正负电荷q构成，分子的电偶极矩为p=ql，当电偶极子的负电荷处于体积l·dS内时，同一偶极子的正电荷就传出界面dS外边。设单位体积分子数为n，则穿出界面的正电荷为：

假如界面S为包围闭合区域V的必和界面，那么穿出的正电荷就是：

由于介质本身是电中性的，因此正电荷的量也等于V内净余的负电荷，而这种由于极化出现的电荷分布称为束缚电荷，用ρ_p来表示束缚电荷密度，就有：

利用高斯公式我们可以得到上式的微分形式：

在介质中，介质的极化产生束缚电荷的分布，而束缚电荷又会激发电场，两者相互制约。因此对于介质中的电荷密度，我们既要考虑自由电荷，也要考虑束缚电荷，根据麦克斯韦方程组，相应的，我们就有：

为了方便书写和讨论，大家就想让这个式子能够简单一些，于是我们将上式通过移项得到：

这里我们引入电位移矢量D，定义为：

这样我们就得到了一个非常简单的关系式：

电位移矢量是一个帮助我们便于讨论的辅助场量，而这个辅助场量显然只和自由电荷密度有关。

为了求解方程，我们还需要知道D和E之间的关系。对于一般各向同性线性介质，我们有：

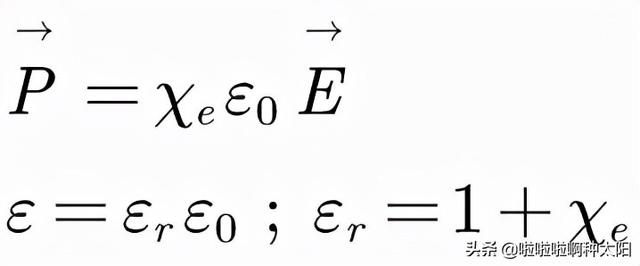
χ_e称为介质的极化率，ε称为介质的电容率，ε_r为相对电容率，将P带入电位移矢量定义式：

---

介质的磁化

介质分子内的电子运动构成微观分子电流，在外磁场的作用下，分子电流的取向将会变得有规则，形成宏观磁化电流密度J_M。微观分子中电子的运动，可以等效成载有电流i，面积矢量为a的电流环。每个电流环都有磁偶极矩：

介质磁化后，出现宏观磁偶极矩分布，用磁化强度M来表示，它定义为ΔV内的总磁偶极矩与ΔV之比：

接下来我们需要求出磁化电流密度J_M。

由图可知，通过S的总磁化电流I_M等于边界线L所

链环着的分子数目乘上每个分子的电流i。因为若分子电流被边界线L链环着，该分子电流就对S的电流有贡献.在其他情形下，或者分子电流根本不通过S，或者从S背面流出来后再从前面流进,所以对I_M没贡献。

若分子位于体积为a·dl的柱体内，则该分子电流就被dl所穿过。假设单位体积内分子数为n，则被边界线L链环着的分子电流数为：

我们将分子电流数目乘以每个分子的电流i：

而根据电流和电流密度的关系，我们不难得到磁化电流和磁化电流密度的关系为：

我们将两式相结合就可以得到：

利用斯托克斯公式，我们就能得到相应的微分形式：

当电场随时间改变时，极化过程中正负电荷的相对位移也将随时间改变，由此产生的电流称为极化电流。假设ΔV内每个带电粒子的位矢位x_i，电荷为e_i，就有：

磁化电流密度和极化电流密度之和是介质内总诱导电流密度，结合上一次我们得出的麦克斯韦方程组，就有：

这里我们要做一个和之前类似的处理来便于讨论，引入辅助场量磁场强度H：

那么我们就有：

通过实验，我们发现对于各向同性非铁磁物质，M和H之间有简单的线性关系：

χ_M称为磁化率：

μ为磁导率，μ_0为相对磁导率。

从物理本质上看，E和B是场的基本物理量，而D和H是辅助物理量，历史上由于人们对于磁场曾有不正确的认识，把H称为磁场强度而和电场强度E对比，现在人们知道这种看法是错误的，但由于历史原因，B和H原来的名称仍然保留了下来。

---

介质中的麦克斯韦方程组

现在我们将自由电荷和自由电流的下角标f略去，将之前得到的式子与原来真空中的麦克斯韦方程组结合，得到介质中的麦克斯韦方程组：

在解决实际问题时，而我们还需要一些电磁性质的实验关系：

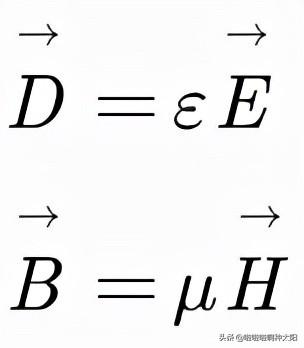
在导电物质中还有欧姆定律：

---

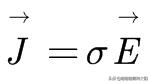
下期预告

麦克斯韦方程组可以用于连续介质内部，但是在介质的分界面上，由于一般出现面电荷电流分布，使物理量发生跃变，微分形式的麦克斯韦方程组不再适用。

因此，在下一期，我们将寻找另一种形式来描述界面两侧场强以及界面上电荷电流的关系。各位对电磁世界好奇的小伙伴，我们下期专题见啦，喜欢的话记得点一下关注哦！

---

编 辑|笨笨

校 对|笨笨

审 核|笨笨

,