中考数学动点小题100道 中考数学中点构造大法

已知题目中出现线段中点或两边倍半关系，要想到的辅助线有：

1、倍长中线

2、等腰三角形三线合一

3、中位线

4、直角三角形斜边上的中线

这讲重点讲解通过构造中位线来解决相关问题

I、通过构造中位线解决线段倍半问题：

先来看上讲的一道课后证明题，

证明三角形重心性质：

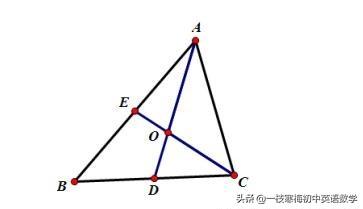
例1、已知：△ABC中，中线AD、CE相交于点O

求证：AO=2DO, CO=2EO

思路：要证线段倍半关系，

可倍长或取中点，

下面用取中点构造中位线证明：

分别取AO、CO中点G、H，

依次连接GEDF，

根据中位线性质

可证DE∥GF，DE=GF，

推得四边形GEDF为“平四”

得：EO=FO=FC,DO=OG=AG

（注：本题也可用倍长或相似证明）

练习1 已知：△ABC中，

点E为中线AD中点，

连BE并延长交 AC 于点 F.

求证：CF=2AF，BE=3EF

提示：

II、通过构造中位线解决中点四边形相关题型：

中点四边形有关结论有：

1、依次连接任意四边形四边中点可得平行四边形

2、依次连接对角线相等的四边形四边中点可得菱形

3、依次连接对角线互相垂直的四边形四边中点可得矩形

4、依次连接对角线相等且互相垂直的四边形四边中点可得正方形

（以上结论易证，由学生自己画图证明并掌握）

例2：已知：OA=OB,OC=OD,

且∠AOB=∠COD=α，

E、 F 、 G 、 H 分别为

AB 、 BC 、 CD 、 DA 边上的中点

（1）求证：四边形 EFGH 为菱形

（2）当 α =___°时，四边形EFGH为正方形

简析：

连对角线

先证明四边形EFGH为“平四”

1、由“手拉手”全等可证AC=BD，再证EH=HG,可得菱形

2、当α=90°时，可证AC⊥BD，可证菱形EFGH为正方形。

例3：已知：RT△ABC中，∠A=90°，D、E分别为

AC、AB边上两动点，

连BD、CE，F、G、M、N分别为BC、DE、CE、BD边上中点

（1）求证：FG=MN

（2）当动点D、E满足什么关系时，FG⊥MN

练习3 已知：正方形ABCD中，E、F、G、H分别为AB、BC、CD、DA边上的点，且EG⊥FH,依次连接EFGH,分别取EF、FG、GH、HE各边中点J、K、L、I，连KI、LJ,

探究线段KI与LJ的关系，并证明.

III、通过构造中位线把分散的边角 集中在一起

例4 已知：四边形ABCD中,M、N分别为AD、BC边的中点，AB=8,CD=6

（1）当∠ABC ∠DCB=90°时，求MN的值.

（2）求：MN的最大值

简析：

（1）连BD,取BD中点H,连HM,HN， 通过导角，可证∠MEN=90°，

勾股得MN=5

声明：图文来源于“以微课堂”，如有侵权请联系删除！

,