高考三角函数基础知识（高考考纲与考向）

考纲原文

1．任意角的概念、弧度制

（1）了解任意角的概念.

（2）了解弧度制的概念，能进行弧度与角度的互化.

2．三角函数

（1）理解任意角三角函数（正弦、余弦、正切）的定义.

知识点详解

一、角的有关概念

1．定义

角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形．

2．分类

（1）按旋转方向不同分为正角、负角、零角．

（2）按终边位置不同分为象限角和轴线角．

3．象限角与轴线角

二、弧度制

1．1弧度的角

把长度等于半径长的弧所对的圆心角叫做1弧度的角．

2．弧度制

3．弧度与角度的换算

4．弧长公式

l=|α|r，其中α的单位是弧度，l与r的单位要统一.

5．扇形的面积公式

三、任意角的三角函数

1．定义

2．三角函数值在各象限内的符号

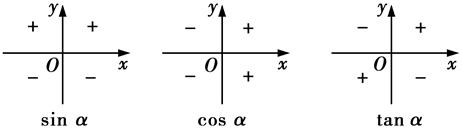
三角函数值在各象限内的符号口诀：一全正、二正弦、三正切、四余弦．

3．三角函数线

设角α的顶点与原点重合，始边与x轴非负半轴重合，终边与单位圆相交于点P，过P作PM垂直于x轴于M．由三角函数的定义知，点P的坐标为(cosα，sinα)，即P(cosα，sinα)，其中cosα=OM，sinα=MP，单位圆与x轴的正半轴交于点A，单位圆在A点的切线与α的终边或其反向延长线相交于点T，则tanα=AT．我们把有向线段OM,MP,AT分别叫做α的余弦线、正弦线、正切线．

各象限内的三角函数线如下：

4．特殊角的三角函数值

补充：

四、同角三角函数的基本关系式

3．同角三角函数基本关系式的变形

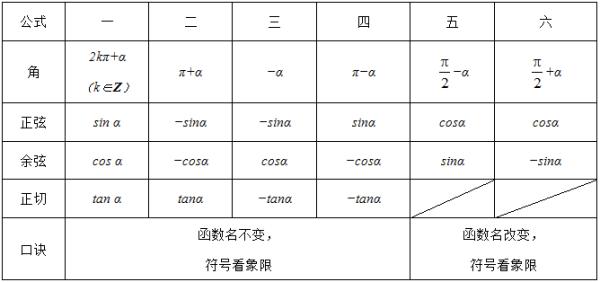
五、三角函数的诱导公式

考向分析

考向一 三角函数的定义

1．利用三角函数的定义求角的三角函数值，需确定三个量：角的终边上任意一个异于原点的点的横坐标x、纵坐标y、该点到原点的距离r.若题目中已知角的终边在一条直线上，此时注意在终边上任取一点有两种情况(点所在象限不同)．

2．利用三角函数线解三角不等式的步骤：①确定区域的边界；②确定区域；③写出解集．

3．已知角α的终边所在的直线方程或角α的大小，根据三角函数的定义可求角α终边上某特定点的坐标．

4．三角函数值的符号及角的位置的判断．已知一角的三角函数值(sinα，cosα，tanα)中任意两个的符号，可分别确定出角的终边所在的可能位置，二者的交集即为该角的终边位置．注意终边在坐标轴上的特殊情况.

【名师点睛】

任意角的三角函数值仅与角α的终边位置有关，而与角α终边上点P的位置无关．若角α已经给出，则无论点P选择在α终边上的什么位置，角α的三角函数值都是确定的．

考向二 象限角和终边相同的角的判断及表示方法

2．象限角的判定有两种方法：

一是根据图象，其依据是终边相同的角的思想；

二是先将此角化为k·360°＋α（0°≤α<360°，k∈Z）的形式，即找出与此角终边相同的角α，再由角α终边所在的象限来判断此角是第几象限角．

3．由角的终边所在的象限判断三角函数式的符号，需确定各三角函数的符号，然后依据“同号得正，异号得负”求解.

【名师点睛】

考向三 同角三角函数基本关系式的应用

考向四 诱导公式的应用

1．应用诱导公式，重点是“函数名称”与“正负号”的正确判断．求任意角的三角函数值的问题，都可以通过诱导公式化为锐角三角函数的求值问题，具体步骤为“负角化正角”→“正角化锐角”→求值．

2．使用诱导公式时一定要注意三角函数值在各象限的符号，特别是在具体题目中出现类似kπ±α的形式时，需要对k的取值进行分类讨论，从而确定出三角函数值的正负．

3．利用诱导公式化简三角函数式的思路：

（1）分析结构特点，选择恰当公式；

（2）利用公式化成单角三角函数；

（3）整理得最简形式．

利用诱导公式化简三角函数式的要求：

（1）化简过程是恒等变形；

（2）结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值．

4．巧用相关角的关系能简化解题的过程．

考向五 同角三角函数的基本关系式、诱导公式在三角形中的应用

,