数据结构树的主要内容（笔记数据结构树）

树的定义

树（tree）是n（n≥0）个节点的有限集合，当n=0时，为空树；n>0时，为非空树。任意一棵非空树，满足以下两个条件：

树的定义

例如，一棵树如图1所示。该树除了树根之后，又分成了3个互不相交的集合T1、T2和T3，这3个集合本身又各是一棵树，称为根的子树。

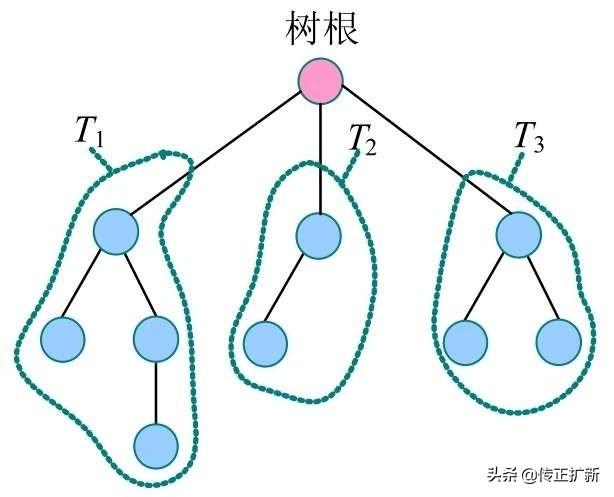
图1 树

该定义是从集合论的角度给出的树的递归定义，即把树的节点看作一个集合。除了树根以外，其余节点分为m个互不相交的集合，每一个集合又是一棵树。

与树相关的术语较多，以下一一介绍：

● 节点——节点包含数据元素及若干指向子树的分支信息。

● 节点的度——节点拥有的子树的个数。

● 树的度——树中节点的最大度数。

● 终端节点——度为0的节点，又称为叶子。

● 分支节点——度大于0的节点。除了叶子都是分支节点。

● 内部节点——除了树根和叶子都是内部节点。

例如，一棵树如图2所示，该树的度为3，其内部节点和终端节点（叶子）均用虚线圈了起来。

图2

● 节点的层次——从根到该节点的层数（根节点为第1层）。

● 树的深度（或高度）——指所有节点中最大的层数。例如，一棵树如图3所示，根为第1层，根的子节点为第2层……该树的最大层次为4，因此树的深度为4。

图3

● 路径——树中两个节点之间所经过的节点序列。

● 路径长度——两节点之间路径上经过的边数。例如，一棵树如图4所示，D到A的路径为D—B—A, D到A的路径长度为2。由于树中没有环，因此树中任意两个节点之间的路径都是唯一的。

图4

如果把树看作一个族谱，就成了一棵家族树，如图5所示。

图5

● 双亲、孩子——节点的子树的根称为该节点的孩子，反之，该节点为其孩子的双亲。

● 兄弟——双亲相同的节点互称兄弟。

● 堂兄弟——双亲是兄弟的节点互称堂兄弟。

● 祖先——从该节点到树根经过的所有节点称为该节点的祖先。

● 子孙——节点的子树中的所有节点都称为该节点的子孙。

祖先和子孙的关系，如图6所示。D的祖先为B、A, A的子孙为B、C、D、E、F、G。

图6

● 有序树——节点的各子树从左至右有序，不能互换位置，如图7所示。

图7

● 无序树——节点各子树可互换位置。

● 森林——由m（m≥0）棵不相交的树组成的集合。

例如，图7中的树在删除树根A后，余下的3个子树构成一个森林，如图8所示。

图8

树的存储结构

树形结构是一对多的关系，除了树根之外，每一个节点有唯一的直接前驱（双亲），除了叶子之外，每一个节点有一个或多个直接后继（孩子）。

采用顺序存储和链式存储两种形式。

1．顺序存储

顺序存储采用一段连续的存储空间，因为树中节点的数据关系是一对多的逻辑关系，不仅要存储数据元素，还要存储它们之间的逻辑关系。

顺序存储分为双亲表示法、孩子表示法和双亲孩子表示法。以图10为例，分别讲述3种存储方法

图10

顺序存储

（1）双亲表示法

双亲表示法，除了存储数据元素之外，还存储其双亲节点的存储位置下标，其中“-1”表示不存在。每一个节点有两个域，即数据域data和双亲域parent，如图9（a）所示。

树根A没有双亲，双亲记为-1, B、C、D的双亲为A，而A的存储位置下标为0，因此，B、C、D的双亲记为0。同样，E、F的双亲为B，而B的存储位置下标为1，因此，E、F的双亲记为1。同理，其他节点也这样存储。

（2）孩子表示法

孩子表示法是指除了存储数据元素之外，还存储其所有孩子的存储位置下标，如图9（b）所示。

图9

A有3个孩子B、C和D，而B、C和D的存储位置下标为1、2和3，因此将1、2和3存入A的孩子域。同样，B有2个孩子E和F，而E和F的存储位置下标为4和5，因此，将4和5存入B的孩子域。因为本题中每个节点都分配了3个孩子域（想一想，为什么？（数的最大度为3））, B只有两个孩子，另一个孩子域记为-1，表示不存在。同理，其他节点也这样存储。

3）双亲孩子表示法

双亲孩子表示法是指除了存储数据元素之外，还存储其双亲和所有孩子的存储位置下标，如图9（c）所示。

此方法其实就是在孩子表示法的基础上增加了一个双亲域，其他的都和孩子表示法相同，是双亲表示法和孩子表示法的结合体。

以上3种表示法的优缺点如下。

双亲表示法只记录了每个节点的双亲，无法直接得到该节点的孩子；孩子表示法可以得到该节点的孩子，但是无法直接得到该节点的双亲，而且由于不知道每个节点到底有多少个孩子，因此只能按照树的度（树中节点的最大度）分配孩子空间，这样做可能会浪费很多空间。双亲孩子表示法是在孩子表示法的基础上，增加了一个双亲域，可以快速得到节点的双亲和孩子，其缺点和孩子表示法一样，可能浪费很多空间。

2．链式存储

由于树中每个节点的孩子数量无法确定，因此在使用链式存储时，孩子指针域不确定分配多少个合适。如果采用“异构型”数据结构，每个节点的指针域个数按照节点的孩子数分配，则数据结构描述困难；如果采用每个节点都分配固定个数（如树的度）的指针域，则浪费很多空间。

可以考虑两种方法存储：一种是采用邻接表的思路，将节点的所有孩子存储在一个单链表中，称为孩子链表表示法；另一种是采用二叉链表的思路，左指针存储第一个孩子，右指针存储右兄弟，称为孩子兄弟表示法。

链式存储

（1）孩子链表表示法

孩子链表表示法表头包含数据元素并指向第一个孩子指针，将所有孩子放入一个单链表中。在表头中，data存储数据元素，first为指向第1个孩子的指针。单链表中的节点记录该节点的下标和下一个节点的地址。仍以图10为例，其孩子链表表示法如图12所示。

图10

图12

A有3个孩子B、C和D，而B、C和D的存储位置下标为1、2和3，因此将1、2和3放入单链表中链接在A的first指针域。同样，B有2个孩子E和F，而E和F的存储位置下标为4和5，因此，将4和5放入单链表中链接在B的first指针域。同理，其他节点也这样存储。

孩子链表表示法中，如果在表头中再增加一个双亲域parent，则为双亲孩子链表表示法。

（2）孩子兄弟表示法

节点除了存储数据元素之外，还有两个指针域lchild和rchild，被称为二叉链表。lchild存储第一个孩子地址，rchild存储右兄弟地址。其节点的数据结构如图13所示。

图13

仍以图10为例，其孩子兄弟表示法如图14所示。

图14

A有3个孩子B、C和D，其长子（第一个孩子）B作为A的左孩子，B的右指针存储其右兄弟C, C的右指针存储其右兄弟D。B有2个孩子E和F，其长子E作为B的左孩子，E的右指针存储其右兄弟F。C有1个孩子G，其长子G作为C的左孩子。D有2个孩子H和I，其长子H作为D的左孩子，H的右指针存储其右兄弟I。G有1个孩子J，其长子J作为G的左孩子。

孩子兄弟表示法的秘诀：长子当作左孩子，兄弟关系向右斜。

信息参考《趣学数据结构》

脑图查看：http://naotu.baidu.com/file/06974e0e847d1c1181ac863424edc03f?token=331132ddf8598156 密码：czkx

是否有帮助 单选

0人 0%

是

0人 0%

否

投票

,