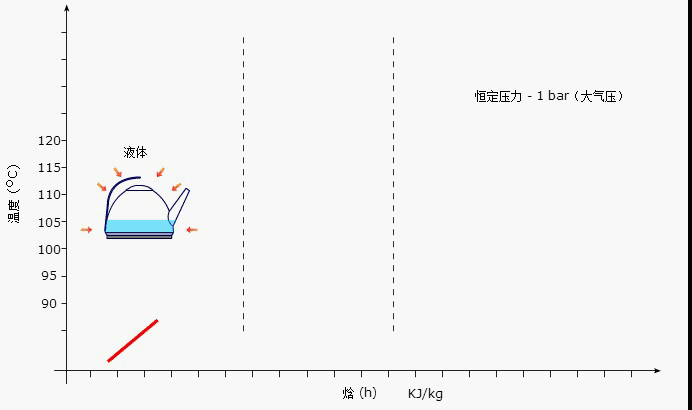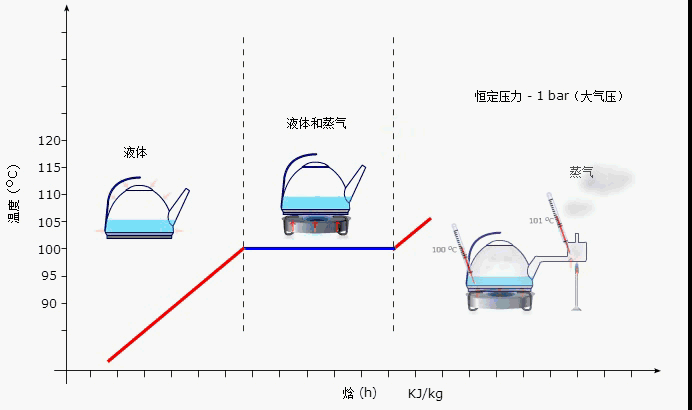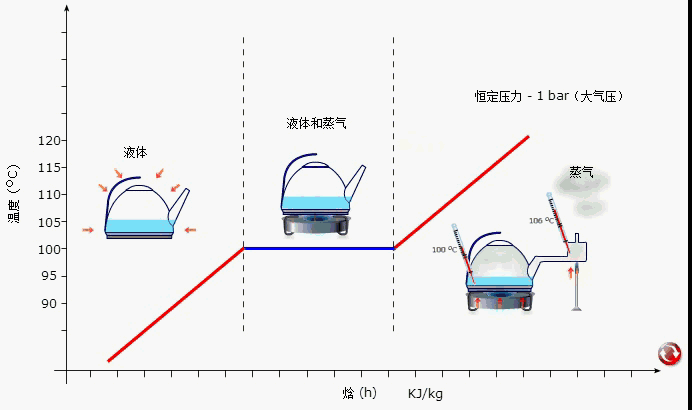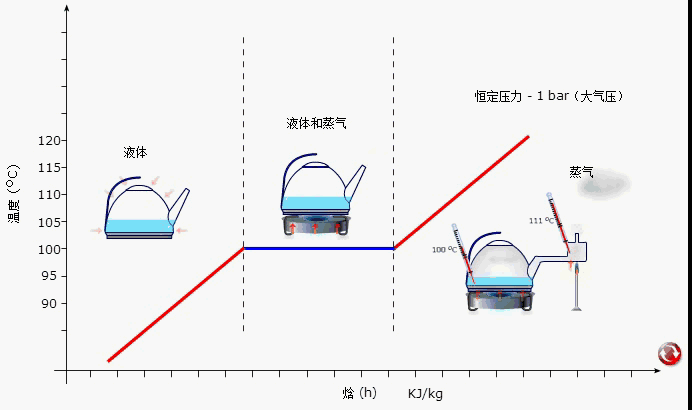
含有未知数的等式叫做方程对不对（含有未知数的等式就是方程）

“x=1是方程，还是方程的解？”这是学生常有的疑惑。

怎么解答这个问题？“因为它符合方程的定义：含有未知数的等式是方程，所以x=1是方程。”

这么说是不是感觉有些牵强？好像是个文字游戏，这样回答对学生理解方程思想有好处吗？

那我如果问：a b=b a是不是方程？C=2πR是不是方程？又该怎么解答？

让我们追根溯源，去了解方程概念的来源。

维基百科上equation的解释是：

In mathematics，an equation is a formula of the form A=B， where A and B are expressions that may contain one or several variables called unknowns，and “=” denotes the equality binary relation.（在数学上，方程是一个形 如A = B的式子，其中A和B是含有一个或几个未知数的表达式，等号“=”表示相等的二元关系）从这个定义看，equation的意思就是等式。

1859年，李善兰(1811-1882)和伟烈亚力(A. Wylie，1815〜1887)合作翻译英国著名数学家德摩根(又译棣么甘，A. De Morgan， 1806〜1871)著的《代数学》(Elements of Algebra)。第一次将equation译成“方程”。

李善兰（图片源于网络）

原文是：“Every collection of algebraical symbols is called an expression，and when two expressions are connected by the sign =，the whole is called an equation.” (A. De Morgan，1837)李善兰和伟烈亚力将这句话译为“并代数之几数名为式，两式之间作等号，谓之方程。”(棣么甘, 1859)

从原文来看，equation就是“将两个代数式用等号连接起来的式子”，依然还是等式的原始本意，并没有任何“未知数”之类的意思。那么为什么李善兰没有将equation直译为“等式”，而是意译为“方程”呢？

再看美国教材：equation一词具有多义性，狭义的理解当然是含有未知数待解的等式，而广义上说就是等式(equality)，都是指两个数量或表达式之间的相等。总体来说，除了“恒等式”(identity)之外，美国数学教材对“等式”基本不作什么解释，因为这是英语里一个浅显易懂的基本单词。而在美国这个十分强调种族和社会平等的体制里，equality (公平，平等)更是大众媒体频繁使用的关键词。equation一词也很类似，时政新闻和评论里经常会有“political equation”，“balance the equation”，“change the equation”之类的措辞，equation一词被赋予，“关联”、“平衡”之义。

从以上三处综合来看，“方程”一词实属中国特色，它将一类用等式表示、并由此求出未知数的模型凸显了出来，比广义的“等式”一词更加准确。英文里的“equation”一词更多是从宏观上强调其“平衡”、“等价”的本质，比较粗泛。如果我们把二者混为一谈是不准确的。

教材中用“含有未知数的等式叫方程”来定义，是受到西方数学教材中对方程定义的影响，而在实际操作中，往往片面地判别为“含有字母的等式叫方程”，那就是谬误了。教师用一堆含有字母的代数式，让学生判别：“是不是等式？”、“有没有字母？”来认识方程。这样做，不会让学生增加任何对方程概念本质属性的认识，很有点“庸人自扰”的味道。试问：有哪个学生因为不认识方程？方程概念一旦脱离寻求未知数这一核心思想，也就远离了它的数学本质。

将“含有未知数的等式”偷换为“含有字母的等式”在逻辑上是错误的。因为“含有字母的等式”种类很多，可以具有不同的意义；而方程只是“含有字母的等式”的一种情形，这个所谓的方程定义，在逻辑上“以偏概全”了。打个比方：“含有字母的等式”好像是一个馒头，你可以拿它当早餐，也可以当午餐、晚餐。馒头的使用目的全凭你而定。说“含有字母的等式叫方程”，就好比“当早餐吃的才叫馒头”，是当然不对的。

再比如：描述加法交换律的式子a b=b a，也是含有字母的等式，但这并不是方程，这个式子中的字母泛指任意数，而不是未知数。圆周长公式C=2πR，这里的字母表示某类数（C表示面积、R表示半径），和方程求未知数没有关系。s=vt当v为常数时，字母表示变量，式子表示两个变量的对应关系。

中国古代，将方程组的各项系数和“实”之数，用算筹布列成矩阵状（现称增广矩阵，这也是“方”字的由来），然后用消元法变换这些系数（“程”就是计量），最后求得问题的解。

增广矩阵（图片源于网络）

刘徽（魏晋时代人，生卒不详）是这样界定方程的：“群物总杂，各列有数，总言其实, 令每行为率。二物者再程，三物者三程，皆如物数程之。立列为行，故谓之方程。”（郭书春, 2004）结合《九章算术》方程章的问题，就可以知道，“方程”二字，其核心思想是借助一组等式关系求出未知数，所面对的是一个多元一次方程组。中国古代在高次方程求解上贡献很大，世称“天元术”。

《九章算术》（图片源于网络）

我们不妨揣测一下李善兰翻译时的良苦用意：可能在他看来，中国的天元术和解线性方程组，都是从一个或一组等式求出那些符号所代表的未知数之值。这样一来，方程就是一种等式关系，但又超出了“等式”原来的含义，中国的“方程” 一词就和“求未知数”、“求满足等式的根”的含义联系在了一起的。由此看来，方程作为最重要的一种等式, 在中国以及东方的汉字文化圈里得到传播，使后学者从中受益，至于仅仅把方程看作“含有字母的等式”，那是过于简单化，辜负了李善兰的一番苦心呀。

再插一个数学之外的“方程”——Fl（FIA Formula 1 World Championship，世界一级方程式锦标赛）。体育赛事怎么也会要解方程呢？原来是参加F1赛事的汽车的气缸、动力、传动、 轮胎等等都要符合一套规定，即一组formula，formula也就顺理成章地翻译成“方程式”。

看来，在长长的科学史上新的科学名词会不断更迭出现，西方文明与东方文明数次交流碰撞，我们绝不能妄自菲薄，照搬照抄，我们应该重视东西方文化的融合，找到西方文化背后的中国背景，让新的概念在博大的中华文化里落地生根。

长按关注哦！