学好二次函数的技巧（掌握了下面的基本知识点）

二次函数：一般地，如果y=ax2 bx c（a，b，c是常数，a≠0），那么y叫做x 的二次函数。对于二次函数，我们需要掌握哪些知识点，我在里向大家介绍一下：

首先，我们了解一下二次函数的一些基本特性：

①所谓二次函数就是说自变量最高次数是2;

②二次函数y=ax2 bx c（a≠0）中x、y是变量，a，b，c是常数，自变量x 的取值范围是全体实数，b和c可以是任意实数，a是不等于0的实数，因为y=ax2 bx c , a=0时，变为y=bx c若b≠0,则y=bx c是一次函数，若b=0，则y=c是一个常数函数。

③二次函数y=ax2 bx c（a≠0）与一元二次方程y=ax2 bx c（a≠0）有密切联系，如果将变量y换成一个常数，那么这个二次函数就是一个一元二次函数。

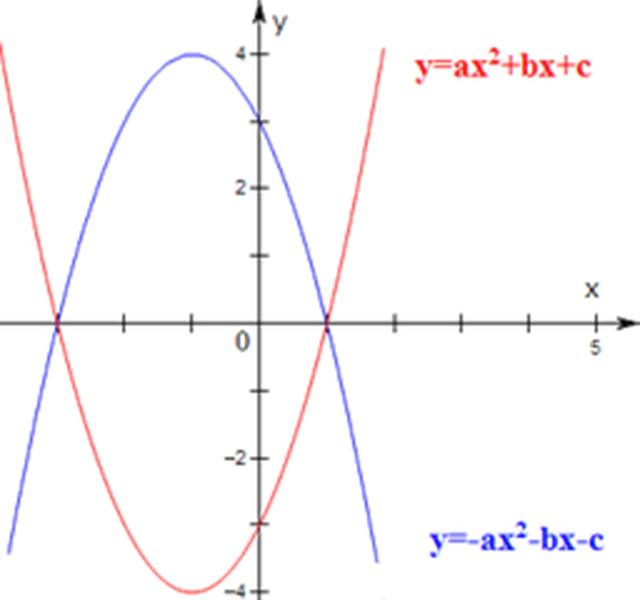
二次函数的解析式有三种形式：

（1）一般式：y=ax2 bx c（a，b，c是常数，a≠0）；

（2）顶点式： y=a(x-h)2 k（a，h，k是常数，a≠0）

（3）当抛物线 : y=ax2 bx c与x轴有交点时，即对应二次好方程ax2 bx c=0

有实根x₁和x₂存在时，根据二次三项式的分解因式 ax2 bx c=a(x-x1)(x-x2)

，二次函数 y=ax2 bx c可转化为两根式 y=a(x-x1)(x-x2)。如果没有交点，则不能这样表示。

二次函数的一般形式的结构特征：

①函数的关系式是整式；

②自变量的最高次数是2；

③二次项系数不等于零。

二次函数的判定：

二次函数的一般形式中等号右边是关于自变量x的二次三项式；

当b=0，c=0时，y=ax²是特殊的二次函数；

判断一个函数是不是二次函数，在关系式是整式的前提下，如果把关系式化简整理（去括号、合并同类项）后，能写成 y=ax2 bx c（a≠0）的形式，那么这个函数就是二次函数，否则就不是。

以上的这些知识点都是二次函数的一些基础知识，希望大家能够掌握，这对大家学好二次函数，会有一定的帮助，这有这样的不对积累，我们才能学好数学，提升我们的成绩，祝大家学习愉快。