gcc基础知识（一文带你入门GCN）

注：本文略过了大部分数学推导，防止掉头发，感兴趣的可自行推导

GCN背景知识

传统CNN只能处理比较简单的序列或网格结构的数据。但是现实世界中很多都是非结构化的，通俗理解就是在拓扑图中每个顶点的相邻顶点数目都可能不同，那么也无法用一个同样尺寸的卷积核来进行卷积运算。

由于CNN无法处理Non Euclidean Structure的数据，但又希望在这样的数据结构（拓扑图）上有效地提取空间特征来进行机器学习，所以GCN成为了研究的重点。

Spectral domain是GCN的理论基础，借助图谱的理论实现拓扑图上的卷积操作，借助拉普拉斯矩阵的特征值和特征向量研究图的性质

Graph上的卷积计算用到了傅立叶变换，而Graph Fourier Transformation及Graph Convolution的定义都用到图的拉普拉斯矩阵，首先介绍一下拉普拉斯矩阵。

拉普拉斯矩阵

对于图G=(V, E) ，其Laplacian 矩阵的定义为$$L=D-A$$ ，其中 L 是Laplacian 矩阵，D是顶点的度矩阵（对角矩阵），对角线上元素依次为各个顶点的度， A是图的邻接矩阵。

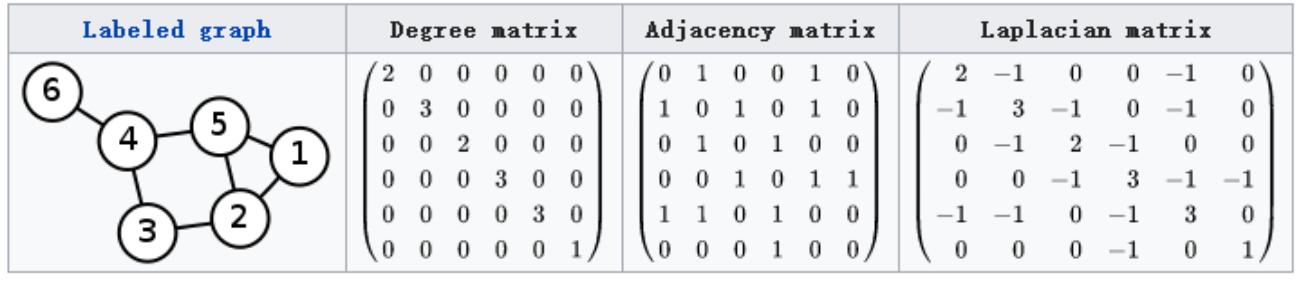
1. $$L=D-A$$定义的Laplacian 矩阵更专业的名称叫Combinatorial Laplacian，上面的图用的是这种计算方法
2. $$L^{sys}=D^{-1/2}LD^{-1/2}$$定义的叫Symmetric normalized Laplacian，很多GCN的论文中应用的是这种拉普拉斯矩阵
3. $$L^{rw}=D^{-1}L$$定义的叫Random walk normalized Laplacian

为什么GCN要用拉普拉斯矩阵？ 拉普拉斯矩阵矩阵有很多良好的性质，

1. 拉普拉斯矩阵是对称矩阵，可以进行特征分解（谱分解），这就和GCN的spectral domain对应上了
2. 拉普拉斯矩阵只在中心顶点和一阶相连的顶点上（1-hop neighbor）有非0元素，其余之处均为0

GCN的核心是基于拉普拉斯矩阵的谱分解，

其中L是拉普拉斯矩阵，U是正交矩阵，中间是n个特征值

傅立叶变换和graph上的傅立叶变换

传统的傅里叶变换定义为：

Graph上的傅立叶变换：

其中$$f(i)$$是Graph上的顶点$$i$$的向量，$$u_l(i)$$表示拉普拉斯矩阵的第$$l$$个特征向量的第$$i$$个分量，$$u_l^{*}(i)$$是$$u_l(i)$$的共轭，$$\lambda_l$$就是第$$l$$个特征值（相当于傅立叶变换的频率）。

$$\hat{f}(\lambda_l)$$的意思就是求f在Graph上做傅立叶变换后，第$$l$$个特征向量（基底）的分量

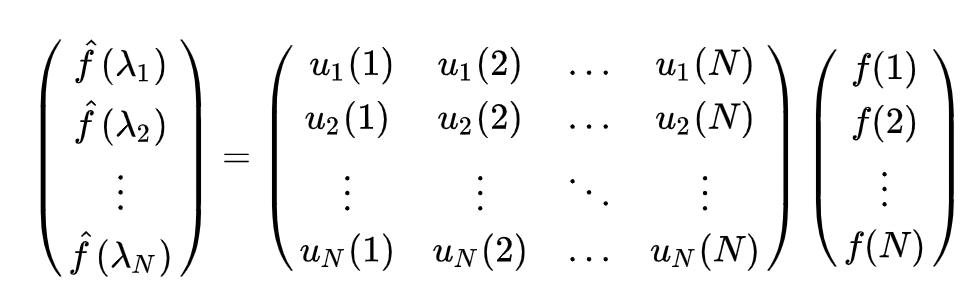
所以f在Graph上的傅立叶变换的矩阵形式为：$$\hat{f} = U^Tf$$，其中$$U$$是拉普拉斯矩阵的单位特征向量的矩阵。

同理，f在Graph上的傅立叶逆变换的矩阵形式为$$f = U\hat{f}$$

Graph上的卷积计算

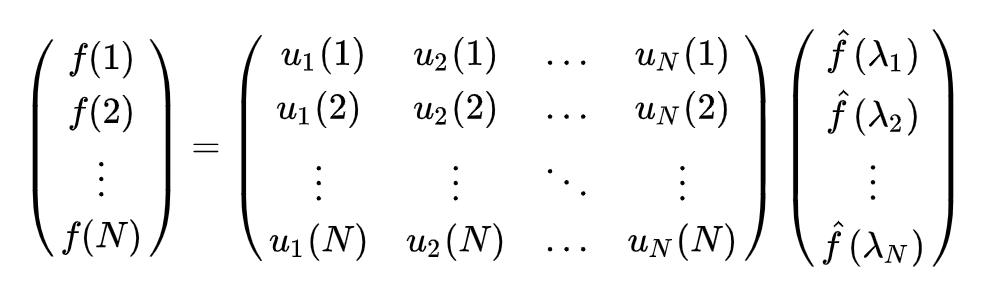
卷积定理：函数卷积的傅里叶变换是函数傅立叶变换的乘积

Graph上的卷积核$$h$$是一个矩阵，下面就是f和h在图上的卷积计算

其中，$$\hat{h}(\lambda_l) = \sum_{i=1}^Nh(i)u_l^*(i)$$是卷积核h在Graph上的傅立叶变换，$$U^Tf$$是f在graph上的傅立叶变换，左乘U是求逆变换

第一代GCN

paper链接

简单粗暴地把$$diag(\hat{h}(\lambda_l))$$作为卷积核$$diag(\theta_l)$$

其中$$g_{\theta}(\Lambda)$$是卷积核，n是顶点个数，$$Ug_{\theta}(\Lambda)U^Tx$$就是卷积运算的结果，x是每个顶点的输入向量，y是每一层的输出

反向传播拟合$$\theta_i$$。

缺点：

1. 每次卷积计算需要计算三个矩阵相乘，复杂度为$$O(n^3)$$
2. 几乎所有卷积核都是稠密的，失去了cnn卷积核的空间局部性。下图是卷积核的例子，图有6个节点

3. 需要n个参数，容易过拟合

第二代GCN

paper链接

计算公式不变，把卷积核设计为

其中，$$\lambda_l^j$$为Graph的第$$l$$个特征值的j次幂，L是Graph的拉普拉斯矩阵，即$$g_\theta(\Lambda) = \sum_{j=0}^K\alpha_j\Lambda^j$$

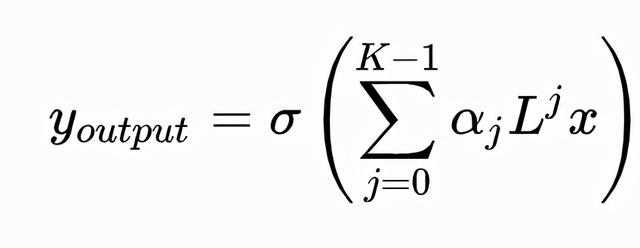
为什么这么设计？

1. 卷积核从n个参数降低成K个参数，K是自定义的参数，K<<n，复杂度降低
2. 公式中的特征矩阵U不需要计算了，不需要做特征分解了。矩阵计算复杂度是$$O(K|E|)$$，其中|E|是边数
3. 卷积核有很好的空间局部性，K代表了卷积核的感受域（回忆下拉普拉斯矩阵的定义），即每次卷积运算会将每个顶点距离为j的特征进行加权求和，权值为$$\alpha_j$$。下面是单个顶点的卷积计算，其中f(i)表示第i个顶点的输入向量

用这个矩阵左乘每个顶点的输入向量即为卷积的运算结果。

缺点：

1. 参数太少，并且不能对不同邻居分配不同权重

第三代GCN

第二代卷积核：$$g_\theta(\Lambda) = \sum_{j=0}^K\alpha_j\Lambda^j$$

用chebyshev多项式拟合卷积核中的$$\Lambda^j$$计算复杂度

第三代卷积积核：$$g_\theta(\Lambda) = \sum_{j=0}^K\alpha_jT_k(\hat{\Lambda})$$

其中$$T_k$$是Chebyshev多项式，$$\hat{\Lambda}=2*\Lambda/\lambda_{max}-I$$，$$\lambda_{max}$$是拉普拉斯矩阵特征值的最大值

第四代GCN

paper链接

第三代卷积计算（$$\theta_k$$是拟合的卷积核参数，L是拉普拉斯矩阵，$$\hat{L}=2*L/\lambda_{max}-I$$，x是顶点的输入向量）：

取$$\lambda_{max}$$= 2，K = 2，有

为了避免过拟合，令$$\theta=\theta_0=-\theta_1$$

模型训练

每一层输入输出都是图结构

以一个半监督文本分类任务为例子，下面这个GCN包括一个隐藏层

数据集是一个论文图，共2708个节点，每个节点都是一篇论文，所有样本点被分为7类别：

Case_Based, Genetic_Algorithms, Neural_Networks, Probabilistic_Methods, Reinforcement_Learning, Rule_Learning, Theory

每篇论文都由一个1433维的词向量表示，即节点特征维度为1433。词向量的每个特征都对应一个词，取0表示该特征对应的词不在论文中，取1则表示在论文中。每篇论文都至少引用了一篇其他论文，或者被其他论文引用，这是一个连通图，不存在孤立点。GCN在训练的时候需要输入整个图，包括测试和验证集样本的结构。

GCN应用

• 半监督人群分类
• 空手道俱乐部是一个包含34个成员的社交网络，有成对的文档交互发生在成员之间。俱乐部后来分裂成两个群体，分别以指导员（节点0）和俱乐部主席（节点33）为首，整个网络可视化如下图：

任务是预测每个节点会加入哪一边。

• 文本分类

• 静态结构图的分类任务
• 预测用户行为是否正常

• GCN(128)->GCN(64)->GCN(64)->Linear(2)

• 人体动作识别
• 人体骨架作为节点

• paper链接，链接2

• 多标签图像识别
• paper链接

• 图像检索

• 。。。

GCN的局限性：

1. GCN在训练的时候需要输入整个图，（如果一个节点代表一个样本，要包括测试和验证集的样本），训练的时候用到所有邻居节点的信息。无法处理新来的节点（处理起来比较tricky），在现实某些任务中也不能实现(比如用今天训练的图模型预测明天的数据，但明天的节点是拿不到的）
2. 无法处理动态图问题
3. 需要将整个图放到内存和显存里，耗费资源
4. 处理有向图比较困难，无法分配不同权重给不同的邻居

其他GNN：GAT，GraphSAGE，VGAE

附录

上文讲的只是GNN中的一小部分，感兴趣的同学可以看看论文

,