初中数学绝对值求解方法（有关绝对值的几个问题）

刚上初一的孩子们会接触到一个新的数学概念：负数。有关复数的运算中，绝对值的问题相对不好理解。下面对有关绝对值的问题做一个简要的探讨。

要首先明白理解概念：一个数或者一个式子的绝对值等于这个数或者这个式子结果的正数值。

比如，a是正数，b是负数，则|a|=a，然而|b|=－b，因为b是负数，－b则是正数。比如，b=－3，－b=－(－3)=3。

再比如，a＋b是正数，c＋d是负数，则|a＋b|=(a＋b)=a＋b，|c＋d|=－(c＋d)=－c－d。我们可以看到，仅判断这个式子的结果是正数还是负数，结果若是正数，则绝对值符号直接变为小括号即可；结果若是负数，则绝对值符号变为小括号后，在小括号前加负号即可。下面我们看一个例题。

解：首先，根据数轴可以判断出a，b为负数，c为正数，且|a|＞|c|＞|b|。

其次，|b|=－b，

|b－a|=(b－a)=b－a，

|a＋c|=－(a＋c)=－a－c，

最后，|b|＋|b－a|－ |a＋c|

=－b＋(b－a)－(－a－c)

=－b＋b－a＋a＋c

=c

同学们，可以带入具体的数字来进行验算。比如a=-5，b=-2，c=3，计算结果为3，即证明解算正确。

咱们再来看一道题来加深理解。

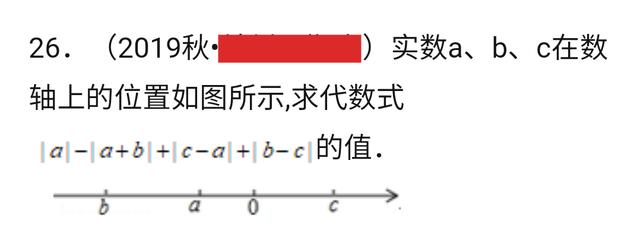
解：首先，根据数轴可以判断出a，b为负数，c为正数，且|b|＞|c|＞|a|。

其次，|a|=－a，

|a＋b|=－(a＋b)=－a－b，

|c－a|=(c－a)=c－a，

|b－c|=－(b－c)=－b＋c，

最后，|a|－|a＋b|＋|c－a|＋|b－c|

=－a－(－a－b)＋(c－a)＋(－b＋c)

=－a＋a＋b＋c－a－b＋c

=2c－a

同样，同学们可以代入具体的数值来检验答案是否正确，比如a=-3，b=-7，c=5代入算式后，计算结果为13，而2c－a=13，即证明解算正确。

关于绝对值的计算就讲解到这里。如果同学们有什么疑问，可私信与我联系。我将尽自己所能为各位同学提供帮助。