空间直角坐标系的两点距离公式（空间两点间不只有空间距离）

• 我的真实姓名叫胡风学，十八岁参加煤矿工作，在煤矿井下干测量工作三十多年。由于煤矿的各项工作都是在通视条件非常有限的立体空间进行，对空间几何做了些许研究，现已退休，把研究感悟发表于此，供大家评判笑谈。别不多说，先谈谈空间点与空间点

• 1.什么是空间点？
• 立体几何书上说“点是只描述而不加定义的原始概念，不能进行度量”。确实，点这个东西我们不能表达它的大小，因为你说它有大小时在平面它就成了园，在空间它就变成球了。并且这个东西宇宙物理学家都发愁，他们说宇宙起源于一次宇宙大爆炸，这个爆炸点叫奇点，这个奇点体积无限小，质量无限大，这个东西到现在我也理解不了。但是，在数学上，在空间几何上，只要利用空间直角坐标系这个平台，理解这个东西就比较方便。

2.空间直角坐标系

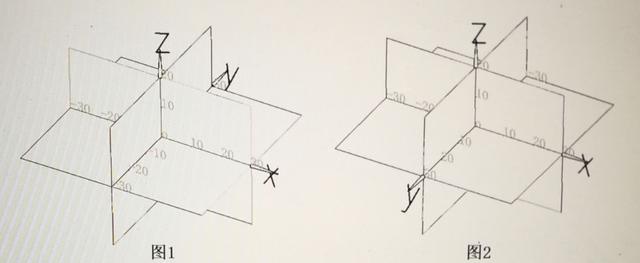
空间直角坐标系就是通过空间任意一点O，作三条互相垂直的直线，并规定其正负方向，他们都以o为原点，具有相同的长度单位，这三条轴分别交x轴，y轴，z轴，通称为坐标轴。并且规定x轴，y轴所在的平面为水平面，z轴是铅垂线。这样三条坐标轴就组成了一个空间直角坐标系。见图1，图2

教材教学时多用图1所示坐标系，大地测量和工程施工中多用图2所示坐标系。

3 空间直角坐标系中的空间点

在空间直角坐标系中，你只要用笔尖轻轻一点，这个点就可以用三个有序数字书写下来。比如图3中的A点，我们分别量取它到三个坐标轴的距离求得其坐标为A（30，10，20） 。

如果我们随意地书写三个有序数字，比如B(—30，25，—20)，我们把它填画到空间直角坐标系中，得图4。这组有序数字，就表示空间直角坐标系中的一个点。

4 空间直角坐标系中两点间的空间距离

我们常说的空间两点间的空间距离见图5。

图5中空间两点间的空间距离就是A、B点之间线段的长度，等于73.6546。

但是，仅仅只知道两点间的空间距离在实际应用中是远远不够的，还需要知道两点间的水平距离，方位角，高差，倾角。

5 空间直角坐标系中两点间的水平距离

大地测量坐标系中空间两点间的水平距离见图6。

图6中，两点间的水平距离A1B1等于61.8466。

6 空间直角坐标系中两点所在直线的方位角

方位角是指大地测量坐标系中已知直线的投影与x轴正方向顺时针旋转的夹角。见图7。

图7中，A，B两点所在直线的投影A1B1方向与x轴的正方向的夹角等于165.9638度。即AB直线的方位角等于165.9638度。

7 空间直角坐标系中两点间的高差

空间直角坐标系中A、B两点间的高差见图8。

图8中，A、B两点的高差等于40.0000。

8 空间直角坐标系中 两点所在直线的倾角

空间直角坐标系中两点所在直线的倾角见图9。

图9中，A、B两点所在直线的倾角等于32.8932度。

9 空间两点坐标在计算工程参数时的应用

图10为某煤矿工程立体示意图，根据需要，需在中央泵房A点与回风巷B点之间开掘回风联巷AB。AB点坐标已知，求在AB点之间开掘巷道的相关参数。 A(95.2290,19.4760,0.0000) B(96.0220,-48.0330,28.8640)

解：本题是传统的各类建筑，开采，隧道工程中常用的由已知两点坐标计算相关工程参数的方法。计算结果见图11。

图11中

10 空间两点的图形类型

图11只是空间两点图形的一种，实际上空间点与空间点在空间直角坐标系中共有4种图形。其图形与数据关系见下表。

11 总结

空间两点间不是仅仅有距离一个数据，两点间存在水平距，方位角，高差，倾角，空间距离五个数据，在施工工程中都非常重要，一个都不能少。

（本文为原创作品，欢迎阅读点赞，关注，转发。反对侵权）

,