素数定理证明论文（正弦定理的源起与应用）

本文为“2022年第四届数学文化征文活动

正弦定理的源起与应用

作者 : 沈乐童

作品编号：052

1. 试题再现

(2019全国Ⅰ理17)的内角A，B，C的对边分别为a，b，c，设

（1）求A；

（2）若，求．

解（1）由已知得

由余弦定理得

因为，所以

（2）由（1）知，由题设及正弦定理得

即

由于，所以，故

2. 史料呈现

正弦定理是三角学中最重要的定理之一，它是直角三角形中边角关系的推广，也是三角形中“大角对大边”这一定性性质的定量刻画。那么首先，我们来思考一下何为“正弦 (Sine)”。

三角学起源于天文学，最早，古希腊天文学家希帕恰斯（Hipparchus，约公 元前 190-120）为了解决天文学中的计算问题，将每一个三角形都当作是圆的内 接三角形，这样三角形的边均变成圆的弦，对角也随之变成弦所对的圆周角（见图1）。

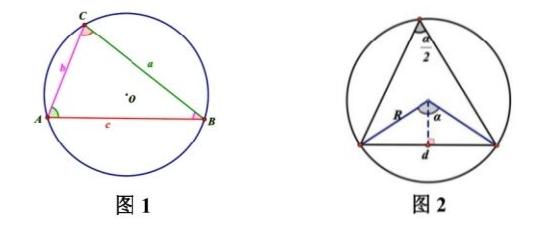
而后托勒密（C. Ptolemy）继承了希帕恰斯的工作，他利用圆半径及弦所对圆周角计算弦长以编制弦表，由图2不难发现，托勒密的“秘密武器”即为这一关系式。几百年后，印度数学家将上式改写成，而阿里亚哈塔（Aryabhata，约 475-550）首次用半弦定义了正弦，这正是正弦“Sine”的词源。

由此可见，所谓的正弦本来就源自圆的弦，而希帕恰斯将三角形看成是圆的 内接三角形的方法深刻地影响了后世数学家对正弦定理乃至整个三角学的研究， 这也就不难理解为什么数学家们会用作外接圆的方法来证明正弦定理。并且，16 世纪以前，正弦（及一切三角函数）均为“线段定义”而非今天所用的“比值定义”。

这是欧洲的普遍说法，那我们再来看看中国古代对于正弦的定义。

图3

正弦是股与弦的比例勾股定理。古代说的“勾三股四弦五”中的“弦”,就是直角三角形中的斜边。股就是人的大腿,长长的,古人称直角三角型中长的那个直角边为“股”。正放的直角三角形,应是大腿站直.正弦是股与弦的比例,余弦是余下的那条直角边与弦的比例。正弦等于股长除弦长。

3. 思考与感悟

数学学习的主要目的是：“在掌握知识的同时，领悟由其内容反映出来的数学思想方法，要在思维能力、情感态度与价值观等多方面得到进步和发展。”数学学习的有效方式是“主动、探究、合作。”现代教育应是开放性教育，师生互动的教育，探索发现的教育，充满活力的教育，以体现数学精神。

但对于学生来说，面对枯燥的数学公式，我们通常处于无感的状态。但通过介绍我们可以知道，正弦定理早在古代就已然存在了，那么这就会引起学生们对于正弦定理的好奇——“正弦定理是怎么来的”、“古代的正弦定理和现代的有什么区别”、“为什么要学习正弦定理”……这些诸如此类的问题便会用现在学生的脑海里。

所以数学这门深奥的，有用的，甚至可以说是奇妙的学科，很值得我们开发大脑去探索。但说数学有用又不仅仅局限于此，作为人类一切科学的源科学，数学与哲学一样能教给人们许多生活的哲理，以及不同的逻辑思维方式。一个好的数学家必定也是一个不凡的哲学家。可以说：数学很大程度上教给人们的不是如何解决问题的方法，而是一种追求真知的信念。所以说，数学很有用，有用的数学才是数学。徐光启译《几何原本》时说：凡同此书者，无事不能通。数学是一门人生学科，需要一生学习。

所以热爱数学吧，它使我们的生活变得更加丰富多彩。

已发文章>>

001 阅读《数学的故事》有感

002 我想和数学谈场恋爱

003 数学“化错”中的美

004 让数学思考成为数学课堂的主旋律

005 卢梭的“错”？

006 数学教学案例《找次品》

007 基于优化学生数学思维的高效课堂创建——以等腰三角形的判定一课为例

008 从特殊到一般，引导数学思维

009 数学文化融入家庭教育的研究

010 sin 震荡函数的图像分析

011 四阶幻方的“太极图”性质

012 无理数的定义和实数理论的建立

013 一个容易被忽视的问题——数学文化

014 “双减”背景下初中数学学科的合作学习方式探究

015 中学数学德育渗透的方法与路径

016 《数学的力量》读后感

017 基于数学文化的单元统整教学设计——以“圆的认识与面积”教学为例

018 有助于数的理解的数字圈环

019 以折叠为例，探究生长型数学教学模式

020 我从事数学科普写作的经验与启示

021 在阅读中滋长智慧——读《教育智慧从哪里来》有感

022 学习数学史 做数学的使者

023 开数学文化之窗 启数学文化魅力——阅读《美丽的数学》有感

024 “文学独白”——数学教学因你而精彩

025 如何用多面体三等分正方体

026 HPM视角下《圆的周长》教学设计

027 被误解的“勾股定理”

028 好玩的数学

029 帮小青蛙设计一个井

030 万物的基础——数学——读《从一到无穷大》有感

031 读《孙子算经》鸡兔同笼问题有感

032 HPM视角下高中数学多样化作业的设计

033 攀越高峰的领路人——数学文化

034 我的好兄弟：数学

035 细嗅数学文化之香

036 藤蔓的喜悦

037 物理力学中数学的影子

038 复数外传

039 函数的历史和发展

040 数学文化与我

041 数学之趣

042 探索数学知识背后的秘密

043 数学文化和我的数学学习

044 古代算数几何形体——阳马与鳖臑

045 数学文化与我的数学学习

046 我与数学文化

,