高中数学必修一知识点详细讲解(高中数学必修一)
第一章 集合与常用逻辑用语
知识点一 集合
1.常用数集及其记法
|
常用数集 |
自然数集 |
正整数集 |
整数集 |
有理数集 |
实数集 |
|
记法 |
N |
N+或N* |
Z |
Q |
R |
2.集合的区间表示
设a,b是两个实数,而且a<b.我们作出规定:
|
集合 |
区间表示 |
区间名称 |
|
{x|a≤x≤b} |
[a,b] |
闭区间 |
|
{x|a<x<b} |
(a,b) |
开区间 |
|
{x|a≤x<b} |
[a,b) |
半开半闭区间 |
|
{x|a<x≤b} |
(a,b] |
半开半闭区间 |
|
集合 |
区间表示 |
|
R |
(-∞,+∞) |
|
{x|x≥a} |
[a,+∞) |
|
{x|x>a} |
(a,+∞) |
|
{x|x≤b} |
(-∞,b] |
|
{x|x<b} |
(-∞,b) |
3.类比实数的大小关系理解集合间的关系
|
实数 |
集合 | |
|
定义 |
a≤b包含两层含义:a=b或a<b |
A⊆B包含两层含义:A=B或A⫋B |
|
相等 |
若a≤b,且b≤a,则a=b |
若A⊆B,B⊆A,则A=B |
|
传递性 |
若a≤b,b≤c,则a≤c |
若A⊆B,B⊆C,则A⊆C |
|
若a<b,b<c,则a<c |
若A⫋B,B⫋C,则A⫋C |
4.有限集合的子集个数
含有n个元素的集合有2n个子集,有(2n-1)个真子集,有(2n-1)个非空子集,有(2n-2)个非空真子集.
5.集合中元素的三个特性
|
特性 |
含义 |
示例 |
|
确定性 |
集合的元素必须是确定的,因此,不能确定的对象不能组成集合,即给定一个集合,任何对象是不是这个集合的元素,应该可以明确地判断出来 |
集合A={1,2,3},则1∈A, 4∉A |
|
互异性 |
对于一个给定的集合,集合中的元素一定是不同的,因此,集合中的任意两个元素必须都是不同的对象,相同的对象归入同一个集合时只能算作集合中的一个元素 |
集合{x,x2-x}中的x应满足x≠x2-x,即x≠0且x≠2 |
|
无序性 |
集合中的元素可以任意排列 |
集合{1,0}和集合{0,1}是同一个集合 |
6.∅的概念及性质
|
概念 |
不含任何元素的集合叫做空集 |
|
性质 |
1.空集是任意一个集合A的子集,即∅⊆A. 2.空集是任意一个非空集合A的真子集,即∅⫋A(A≠∅) |
7.集合的基本运算
|
并集的 概念 |
A∪B={x|x∈A或x∈B} |
|
并集的 性质 |
(1)①A⊆(A∪B),B⊆(A∪B);②A∪A=A,A∪∅=A;③A∪B=B∪A; ④(A∪B)∪C=A∪(B∪C); (2)若A⊆B,则A∪B=B;反之,若A∪B=B,则A⊆B |
|
交集的 概念 |
A∩B={x|x∈A且x∈B} |
|
交集的 性质 |
(1)①(A∩B)⊆A,(A∩B)⊆B;②A∩A=A,A∩∅=∅;③A∩B=B∩A; ④(A∩B)∩C=A∩(B∩C); ⑤(A∩B)∪C=(A∪C)∩(B∪C),(A∪B)∩C=(A∩C)∪(B∩C); (2)若A⊆B,则A∩B=A;反之,若A∩B=A,则A⊆B |
|
补集的概念 |
∁UA={x|x∈U且x∉A} |
|
补集的 性质 |
(1)∁UU=∅,∁U∅=U,∁U(∁UA)=A,A∪(∁UA)=U,A∩(∁UA)=∅; (2)若A⊆B,则∁UA⊇∁UB;反之,若∁UA⊇∁UB,则A⊆B; (3)若A=B,则∁UA=∁UB;反之,若∁UA=∁UB,则A=B; (4)①∁U(A∩B)=(∁UA)∪(∁UB);②∁U(A∪B)=(∁UA)∩(∁UB) |
知识点二 常用逻辑用语
1.全称量词命题与存在量词命题的否定
|
命题类型 |
否定 |
|
存在量词命题:∃x∈M,p(x) |
否定为全称量词命题:∀x∈M,¬p(x) |
|
全称量词命题:∀x∈M,q(x) |
否定为存在量词命题:∃x∈M,¬q(x) |
|
命题p |
命题p的否定(¬p) |
|
真 |
假 |
|
假 |
真 |
2.常见的否定词语
|
正面词语 |
= |
>(<) |
是 |
都是 |
任意(所有) |
存在 |
至多有1个 |
至少有1个 |
或 |
且 |
|
否定词语 |
≠ |
≤(≥) |
不是 |
不都是 |
某个 |
不存在 |
至少有2个 |
1个也没有 |
且 |
或 |
3.充分条件与必要条件
|
p与q满足的关系 |
p是q的________条件 |
|
p⇒q且q不能推出p |
充分不必要 |
|
p能推出q且q⇒p |
必要不充分 |
|
p⇒q且q⇒p(p⇔q) |
充要 |
|
p能推出q 且q能推出p |
既不充分也不必要 |
第二章 等式与不等式
知识点 等式与不等式
1.等式与不等式的性质
|
等式的 性质 |
文字语言 |
符号语言 | |||
|
性质1 |
等式的两边同时加上同一个数或代数式,等式仍成立 |
如果a=b,那么对任意c,都有a+c=b+c | |||
|
性质2 |
等式的两边同时乘以同一个不为零的数或代数式,等式仍成立 |
如果a=b,那么对任意不为零的c,都有ac=bc | |||
|
不等式的性质 |
别名 |
性质内容 |
注意 | ||
|
性质1 |
可加性 |
如果a>b,那么a+c>b+c |
可逆 | ||
|
性质2 |
可乘性 |
如果a>b,c>0,那么ac>bc |
c的符号 | ||
|
性质3 |
可乘性 |
如果a>b,c<0,那么ac<bc |
c的符号 | ||
|
性质4 |
传递性 |
如果a>b,b>c,那么a>c |
同向 | ||
|
性质5 |
对称性 |
a>b⇔b<a |
可逆 | ||
|
推论1 |
移项法则 |
如果a+b>c,那么a>c-b |
可逆 | ||
|
推论2 |
同向可加性 |
如果a>b,c>d,那么a+c>b+d |
同向 | ||
|
推论3 |
同向同正可乘性 |
如果a>b>0,c>d>0,那么ac>bd |
同向同正 | ||
|
推论4 |
可乘方性 |
如果a>b>0,那么a的n次方>b的n次方(n∈N,n>1) |
同正 | ||
|
推论5 |
可开方性 |
如果a>b>0,那么a的算数平方根>b的算数平方根 |
同正 | ||
2.等式与不等式的运用
|
比较大小的方法 |
方法 |
依据 |
应用范围 |
|
作差法 |
a-b>0⇔a>b; a-b=0⇔a=b; a-b<0⇔a<b |
整式、分式的大小比较 | |
|
比较大小的方法 |
作商法 |
a>0,b>0, 则a/b>1⇔a>b; a/b=1⇔a=b; a/b<1⇔a<b |
乘积式、指数式的大小比较 |
|
a<0,b<0, 则a/b>1⇔a<b; a/b=1⇔a=b; a/b<1⇔a>b | |||
|
乘方法 |
a的平方>b的,且a>0,b>0⇒a>b |
无理数(式)的大小比较 | |
|
十字相乘法 |
对于二次三项式Ex2+Fx+G,如果能找到a,b,c,d,使得E=ac,G=bd,且F=ad+bc,则Ex2+Fx+G=(ax+b)(cx+d) | ||
|
一元二次方程根与系数的关系 |
如果一元二次方程ax2+bx+c=0(a≠0)的两根是x1,x2,那么x1+x2=-b/a,x1x2=c/a | ||
3.常用结论
|
重要不等式 |
a^2+b^2≥2ab,当且仅当a=b时,等号成立 |
|
基本不等式 |
(a b)/2≥√ ̄(ab)(a>0,b>0),当且仅当a=b时,等号成立 |
|
最值定理 |
设x,y都是正数. (1)若x+y=S(和为定值),则当x=y时,积xy取得最大值; (2)若xy=P(积为定值),则当x=y时,和x+y取得最小值. 说明:应用均值不等式求最值的条件为“一正、二定、三相等” |
第三章 函数
知识点一 函数的图像
|
函数的图像变换 |
平移变换 |
①函数y=f(x+a)(a≠0)的图像可以由函数y=f(x)的图像沿x轴向左(a>0)或向右(a<0)平移|a|个单位长度得到; ②函数y=f(x)+a(a≠0)的图像可以由函数y=f(x)的图像沿y轴向上(a>0)或向下(a<0)平移|a|个单位长度得到 |
|
对称变换 |
①函数y=f(-x)的图像可由函数y=f(x)的图像作关于y轴的对称变换得到; ②函数y=-f(x)的图像可由函数y=f(x)的图像作关于x轴的对称变换得到; ③函数y=-f(-x)的图像可由函数y=f(x)的图像作关于原点的对称变换得到 | |
|
翻折变换 |
①作函数y=f(|x|)的图像,可先作函数y=f(x)的图像,保留函数y=f(x)的图像在y轴上及y轴右侧的部分,并将y轴左侧的图像换成y轴右侧的图像沿y轴翻折而成的图像即可; ②作函数y=|f(x)|的图像,可先作函数y=f(x)的图像,保留函数y=f(x)的图像在x轴上及x轴上方的部分,并将x轴下方的部分沿x轴翻折到x轴上方即可 |
知识点二 函数的单调性
|
条件 |
一般地,设函数y=f(x)的定义域为D,且I⊆D,如果对任意x1,x2∈I,当x1<x2时,都有 | |
|
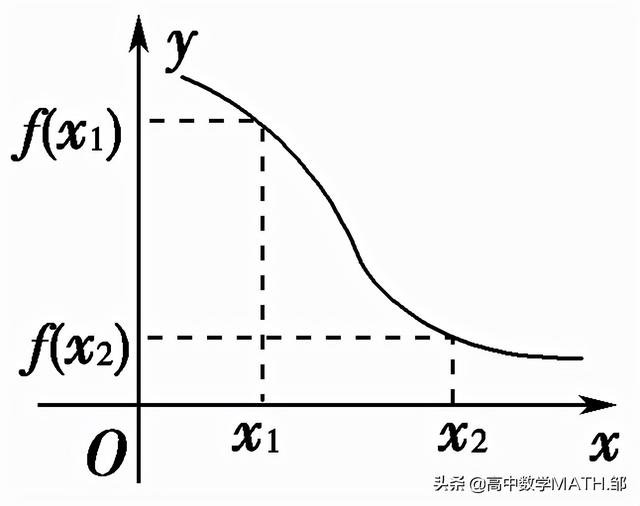
f(x1)<f(x2) |
f(x1)>f(x2) | |
|
结论 |
则称y=f(x)在I上是增函数(也称在I上单调递增) |
则称y=f(x)在I上是减函数(也称在I上单调递减) |
|
图示 |
自左向右图像逐渐上升 |
自左向右图像逐渐下降 |
|
判断方法 |
任取x1,x2∈D,x1≠x2,那么当x1<x2时,f(x1)<f(x2)⇔(x1-x2)[f(x1)-f(x2)]>0⇔>0⇔f(x)在区间D上单调递增; 当x1<x2时,f(x1)>f(x2)⇔(x1-x2)[f(x1)-f(x2)]<0⇔<0⇔f(x)在区间D上单调递减 | |
1.常见函数的单调性
|
函数 |
单调性 |
|
一次函数y=ax+b(a≠0) |
a>0时,在R上单调递增; a<0时,在R上单调递减 |
|
反比例函数y=(a≠0) |
a>0时,单调递减区间是(-∞,0)和(0,+∞); a<0,单调递增区间是(-∞,0)和(0,+∞) |
|
二次函数y=a(x-m)2+n(a≠0) |
a>0时,单调递减区间是(-∞,m],单调递增区间是[m,+∞); a<0时,单调递减区间是[m,+∞),单调递增区间是(-∞,m] |
|
对勾函数y=x+(p>0) |
单调递增区间是(-∞,-]和[,+∞),单调递减区间是[-,0)和(0,].
|
2.单调函数的运算性质
|
f(x) |
g(x) |
f(x)+g(x) |
f(x)-g(x) |
|
增函数 |
增函数 |
增函数 |
不能确定单调性 |
|
增函数 |
减函数 |
不能确定单调性 |
增函数 |
|
减函数 |
减函数 |
减函数 |
不能确定单调性 |
|
减函数 |
增函数 |
不能确定单调性 |
减函数 |
3.函数的最值
|
最大值 |
最小值 | |
|
定义 |
一般地,设函数f(x)的定义域为D,且x0∈D:如果对任意x∈D,都有f(x)≤f(x0),则称f(x)的最大值为f(x0),而x0称为f(x)的最大值点 |
一般地,设函数f(x)的定义域为D,且x0∈D:如果对任意x∈D,都有f(x)≥f(x0),则称f(x)的最小值为f(x0),而x0称为f(x)的最小值点 |
|
几何意义 |
函数的最大值对应其图像最高点的纵坐标 |
函数的最小值对应其图像最低点的纵坐标 |
|
常用 结论 |
(1)如果函数y=f(x)在区间[a,b]上单调递增,那么函数y=f(x),x∈[a,b]在x=a处取得最小值,在x=b处取得最大值; (2)如果函数y=f(x)在区间[a,b]上单调递减,那么函数y=f(x),x∈[a,b]在x=a处取得最大值,在x=b处取得最小值; (3)如果函数y=f(x)在区间[a,b]上单调递增,在区间[b,c]上单调递减,那么函数y=f(x),x∈[a,c]在x=b处取得最大值; (4)如果函数y=f(x)在区间[a,b]上单调递减,在区间[b,c]上单调递增,那么函数y=f(x),x∈[a,c]在x=b处取得最小值 | |
知识点三 函数的奇偶性
1.函数的奇偶性
|
定义 的等 价式 |
奇函数定义的等价式:f(-x)=-f(x)⇔f(-x)+f(x)=0或=-1(f(x)≠0); 偶函数定义的等价式:f(-x)=f(x)⇔f(-x)-f(x)=0或=1(f(x)≠0) |
|
常 用 结 论 |
(1)如果一个奇函数在原点处有定义,那么一定有f(0)=0.有时可以用这个结论来判定一个函数不是奇函数; (2)奇函数的图像关于原点对称,且在关于原点对称的区间上有相同的单调性;偶函数的图像关于y轴对称,且在关于原点对称的区间上有相反的单调性.上述结论可简记为“奇同偶异” |
2.奇偶函数的运算性质及复合函数的奇偶性
设非零函数f(x),g(x)的定义域分别是F,G,若F=G,则有下列结论:
|
f(x) |
g(x) |
f(x)+g(x) |
f(x)-g(x) |
f(x)g(x) |
f[g(x)] |
|
偶函数 |
偶函数 |
偶函数 |
偶函数 |
偶函数 |
偶函数 |
|
偶函数 |
奇函数 |
不能确定奇偶性 |
奇函数 |
偶函数 | |
|
奇函数 |
偶函数 |
奇函数 |
偶函数 | ||
|
奇函数 |
奇函数 |
奇函数 |
奇函数 |
偶函数 |
奇函数 |
注意:上述表格中不考虑f(x)±g(x)=0;f[g(x)]中,需x∈G,g(x)∈F.
3.函数图像的对称性
|
轴 对 称 |
函数y=f(x)在定义域内恒满足的条件 |
函数y=f(x)的图像的对称轴 |
|
f(a+x)=f(a-x) |
直线x=a | |
|
f(x)=f(a-x) |
直线x= | |
|
f(a+x)=f(b-x) |
直线x= | |
|
中 心 对 称 |
函数y=f(x)在定义域 内恒满足的条件 |
函数y=f(x)图像 的对称中心 |
|
f(a+x)+f(a-x)=2b |
点(a,b) | |
|
f(x)+f(a-x)=b |
点 | |
|
f(a+x)+f(b-x)=c |
点 |
知识点四 函数与方程、不等式之间的关系
|
零点的意义 |
方程f(x)=0有实数根⇔函数y=f(x)的图像与x轴有交点⇔函数y=f(x)有零点 |
|
函数零 点存在 定理 |
如果函数y=f(x)在区间[a,b]上的图像是连续不断的,并且f(a)f(b)<0(即在区间两个端点处的函数值异号),则函数y=f(x)在区间(a,b)中至少有一个零点,即∃x0∈(a,b),f(x0)=0 |
|
二分法 |
二分法的解题原理是函数零点存在定理. 通过二分法使有解区间逐步缩小,体现“无限逼近思想” |
1.二次函数与一元二次方程、不等式的对应关系
|
Δ>0 |
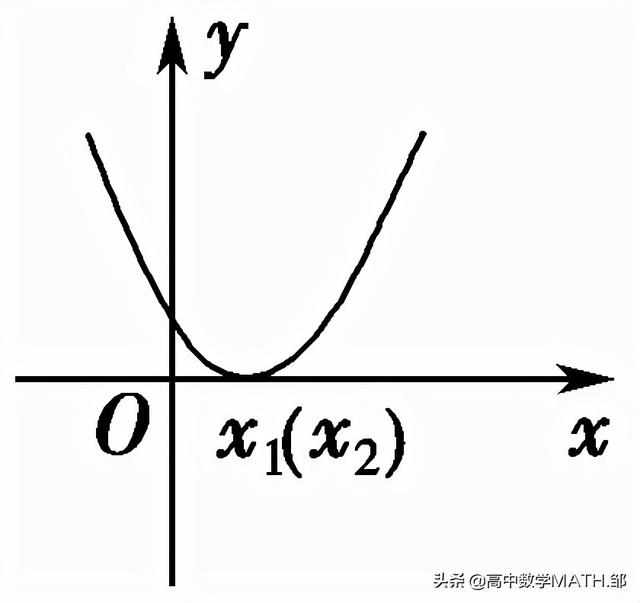
Δ=0 |
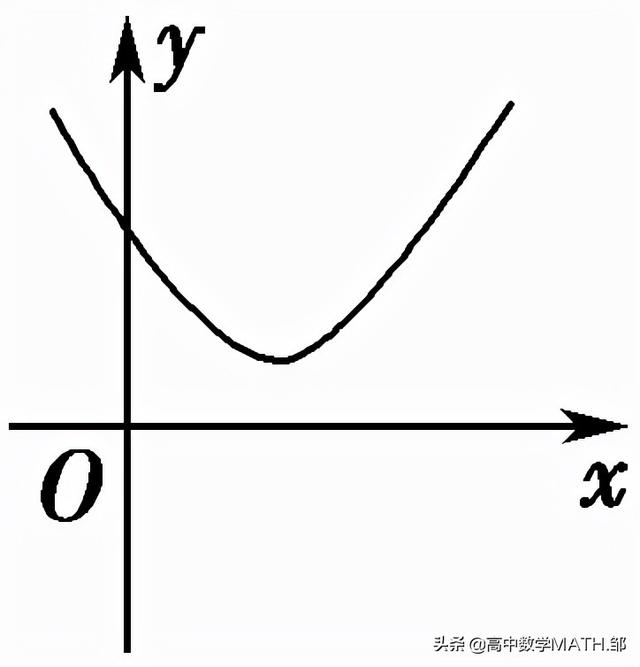
Δ<0 | ||
|
二次函数 y=ax2+bx+c (a>0)的图像 |
|
|
| |
|
一元二次方程 ax2+bx+c=0 (a>0)的根 |
有两个相异的实数根x1=, x2= |
有两个相等的实数根x1=x2=- |
没有实数根 | |
|
一元 二次 不等 式的 解集 |
ax2+bx +c>0 (a>0) |
{x|x<x1或x>x2} |
{x∈R|x≠-} |
R |
|
ax2+bx+c<0 (a>0) |
{x|x1<x<x2} |
∅ |
∅ | |
2.不等式恒成立问题的解法
(1)a≠0时,ax2+bx+c>0(<0)对任意实数x恒成立的条件是().
(2)对于参数较易分离且分离后函数的最值易求的问题都可以采用分离参数法,其常用的结论是:g(a)>f(x)(g(a)<f(x))恒成立等价于g(a)>f(x)max(g(a)<f(x)min).
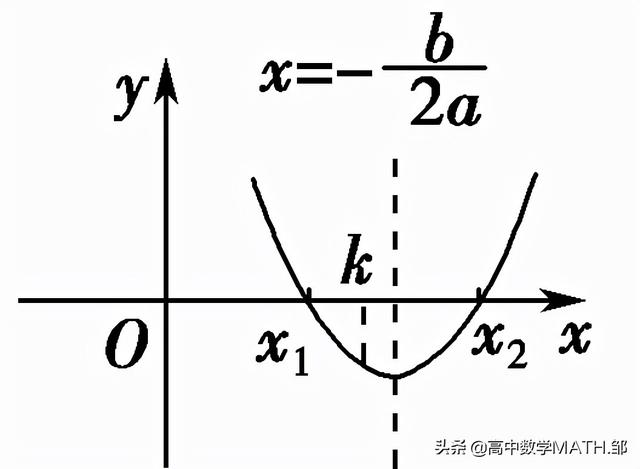
3.方程f(x)=0(f(x)=ax2+bx+c,a>0)的根的分布问题
|
根的分布 |
图像 |
所需条件 |
|
x1<x2<k |
| |
|
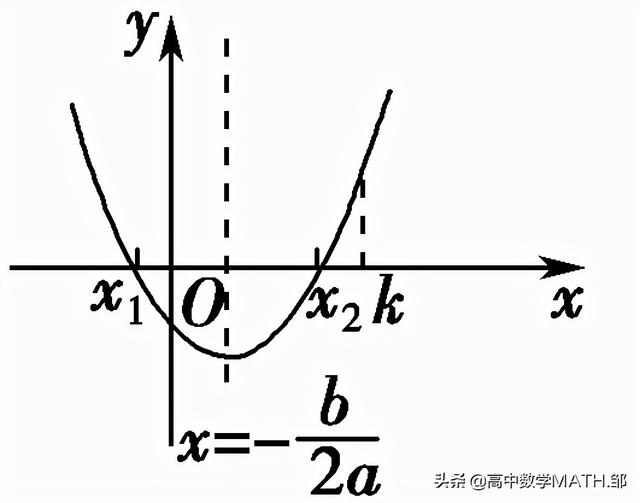
k<x1<x2 |
| |
|
x1<k<x2 |
|
f(k)<0 |
|
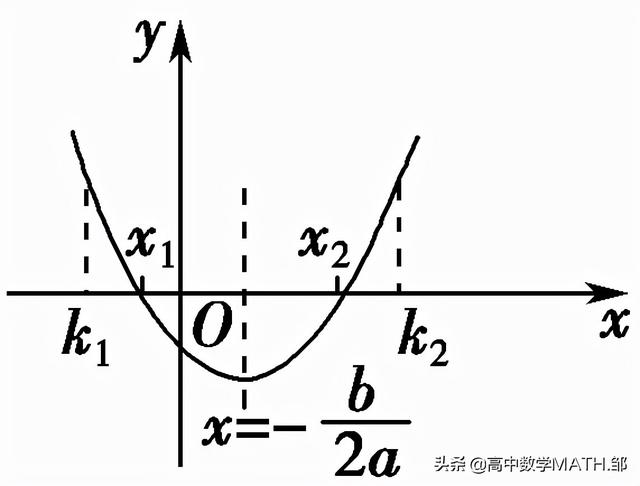
x1,x2∈(k1,k2) |
| |
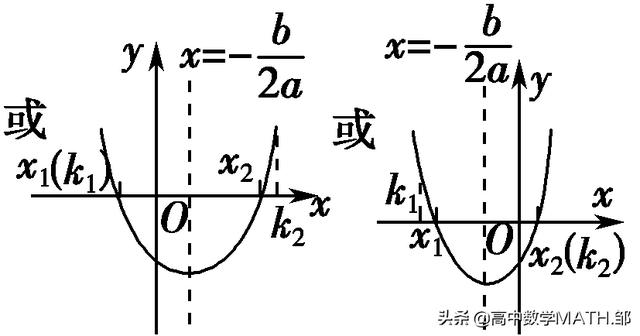
|
x1,x2中有且仅有一个在(k1,k2)内 |
|
f(k1)f(k2)<0或f(k1)=0,k1<-<或f(k2)=0,<-<k2 |
免责声明:本文仅代表文章作者的个人观点,与本站无关。其原创性、真实性以及文中陈述文字和内容未经本站证实,对本文以及其中全部或者部分内容文字的真实性、完整性和原创性本站不作任何保证或承诺,请读者仅作参考,并自行核实相关内容。文章投诉邮箱:anhduc.ph@yahoo.com