为啥现在的解方程那么复杂（解方程的历史与近世代数起源）

解方程是一项古老又迷人并且极具数学趣味性的智力游戏。通过回溯人类解方程的历史，可以窥见数学发展历史的一些蛛丝马迹。

Long long ago，人们还没有分数的概念，直到最先接触到形如ax b=0的一元一次方程（a肯定是不等于0），求根公司为x=-b/a，为了简单起见，人为定义了分数（两个整数之比）。

再后来，解一元二次方程（形如ax^2 bx c=0），人们得到的求根公式中涉及到开方，但是经常遇到根号下的数为负数的情况，于是人们引入了虚数的概念，从而将数域从实数扩充到复数。

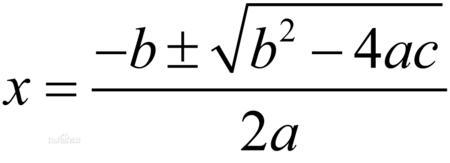
一元二次方程求根公式

再后来，一元三次方程和一元四次方程的求根公式都被陆续被找到了，于是数学家们信心大增，认为一元五次方程的求根公式很快就会被找出来。于是他们义无反顾踏上了寻找一元五次方程的求根公式之旅……然而几百年过去了，无数的数学家纷纷折戟而归，这个问题依然悬而未解。

一元四次方程求根公式

有些人依旧孜孜不倦的在寻找答案，而年轻的法国数学家伽罗瓦则打算另辟蹊径，他猜想万一本一元五次方程本来就不存在求根公式呢？如果说能发展出一套理论用于判断任意次方程能否存在求根公式就好了。后来他用‘群’的思想证明了他的想法是对的，从而一下子解决了这个世界难题。后人受他启发，逐渐完善了群论，而这也正是近世代数的重要起源。为了纪念他开创了群论，伽罗瓦群就是以他的名字命名的。

法国数学家伽罗瓦

他是第一个提出「群」的思想的数学家，一般称他为近世代数创始人。他使代数学由作为解 的科学转变为研究代数运算结构的科学，即把代数学由 时期推向抽象代数即近世代数时期。

围绕着人类解方程的历史，会发现数学大厦正变得越来越完善了，首先体现在数域扩充上面，从自然数集拓展到整数集，再到实数集，最后再到复数集，其次在研究方法上由静态分析到微积分的发现，数学开始运动起来，后来为了解决“最速降线”问题，发展出了“变分法”思想，再从简单代数到后来发现群论，开始研究抽象代数（也就是近世代数）……

发展到现在，数学的水已经非常深了，不信的话可以看看下面这张图“数学的深渊”

数学的深渊

为什么我们有时候觉得数学没那么难，不就加减乘除解方程吗？我们的迷之自信从哪里来？这其实是因为著名的“达克效应”。 达克效应（D-K effect），全称为邓宁-克鲁格效应（Dunning-Kruger effect）。它是一种 现象，指的是能力欠缺的人在自己欠考虑的决定的基础上得出错误结论，但是无法正确认识到自身的不足，辨别错误行为。这些能力欠缺者们沉浸在自我营造的虚幻的优势之中，常常高估自己的能力水平，却无法客观评价他人的能力。

达克效应

希望我们能认清自己，对未知充满敬畏，努力拓展自己的知识边界，只有站在更高的位置，才能意识到自己的微不足道，学会谦卑。

如果说对数学有着浓厚的兴趣，可以读一下吴军写的《数学之美》这本书，书中将高深的数学原理讲得更加通俗易懂，让非专业读者也能领略数学的魅力。通过具体实例教会读者在解决问题时如何化繁为简，如何用数学去 工程问题，如何跳出固有思维不断去思考创新等。