知道均值和方差求无偏估计（话说数据科学数学技能之均值）

本期我们来简单了解一下均值（mean）和方差（variance）这两个概念，同样我们会在西格玛运算这一背景之下来进行说明。

均值（mean）

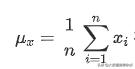
在这个等式的左侧使用符号来表示均值，其右下侧的x表示一个集合，故所表达的是集合x中所有数之和的均值。通过等式右侧的表达式可知，在集合x中有n个数，集合x的所有数之和表示为

，即

的计算结果，因此其均值为所有数的总和除以数字的个数n。

我们举一个简单的例子来看一下，假设有一个集合A，该集合中有三个实数如下：

A={1，5，12}，其集合A的绝对值为|A|=3，说明该集合有三个实数。

集合A的均值计算过程为：

，因此=6。

在了解均值的基础上，我们延伸到另外一个概念——均值中心化，简单来说，可以理解为将我们所计算出的当前均值作为中心点（“0”）来看待。例如当集合A的均值“6”作为中心点来看的话，相应的集合A的所有数字均需相应地进行位移。

均值中心化这一概念会在线性回归中应用到，对于数据分析也是很重要的一个技巧，在之后相关的内容中，我们会进一步介绍。

至于为何要提出均值这一概念，我们可以这样去理解，如果遇到一个体量非常大的数据集合，均值或许是我们能总结该数据集信息的最简单方式，毕竟这个均值是可以给我们提供一定的信息的。

方差（variance）

虽然均值在一定程度上可以提供关于数据集的信息，但并不总是如此。例如，以下两个集合：

A={1，5，12}，B={5，6，7}

和经计算后，两个集合的均值都是6，但实际上两个集合是不一样的，因此我们也需要其他的判断方式或工具来帮助我们进行数据集的区分。

如果在实数轴上来看这两个集合，会发现集合B的延展性更大。

如何知道其延展性具体是多少，我们可以通过方差来进行对比。

等式左侧用表示集合X的方差，右侧表达式取集合X中每个数与均值差的平方之和，最后除以集合X所有数的个数或其绝对值n。

这里为何使用集合X中各个数字与均值差的平方，是考虑到差会有负数的情况，例如在集合A中，均值左侧的数字1和5与均值相减得到就是负数，而我们实际要知道的是该数与均值之间的距离，通过平方就可解决这一问题。

根据以上等式，我们来计算一下所给的两个集合A和B的方差。

比较之下，集合A的方差远远大于集合B，从而也印证了在实数轴上它的延展性更大。尽管两个集合的均值相同，但是其方差或标准差不一样，这对于我们在进行数据分析时是个很好的判断工具，比较两个数据集的差别。