pso算法和bp神经网络（TomasoPoggio深度学习理论深度网络）

笑话衬心 2022-12-04 19:26:05

选自arXiv，作者：Tomaso Poggio等，机器之心编译，参与：路、李亚洲、刘晓坤。

本文是 DeepMind 创始人 Demis Hassabis 和 Mobileye 创始人 Amnon Shashua 的导师、MIT 教授 Tomaso Poggio 的深度学习理论系列的第三部分，分析深度神经网络的泛化能力。该系列前两部分讨论了深度神经网络的表征和优化问题，机器之心之前对整个理论系列进行了简要总结。在深度网络的实际应用中，通常会添加显性（如权重衰减）或隐性（如早停）正则化来避免过拟合，但这并非必要，尤其是在分类任务中。在本文中，Poggio 讨论了深度神经网络的过拟合缺失问题，即在参数数量远远超过训练样本数的情况下模型也具备良好的泛化能力。其中特别强调了经验损失和分类误差之间的差别，证明深度网络每一层的权重矩阵可收敛至极小范数解，并得出深度网络的泛化能力取决于多种因素的互相影响，包括损失函数定义、任务类型、数据集类型等。

1 引言

过去几年来，深度学习在许多机器学习应用领域都取得了极大的成功。然而，我们对深度学习的理论理解以及开发原理的改进能力上都有所落后。如今对深度学习令人满意的理论描述正在形成。这涵盖以下问题：1）深度网络的表征能力；2）经验风险的优化；3）泛化——当网络过参数化（overparametrized）时，即使缺失显性的正则化，为什么期望误差没有增加？

本论文解决了第三个问题，也就是非过拟合难题，这在最近的多篇论文中都有提到。论文 [1] 和 [7] 展示了线性网络的泛化特性可被扩展到 DNN 中从而解决该难题，这两篇论文中的泛化即用梯度下降训练的带有特定指数损失的线性网络收敛到最大间隔解，提供隐性的正则化。本论文还展示了同样的理论可以预测经验风险的不同零最小值（zero minimizer）的泛化。

2 过拟合难题

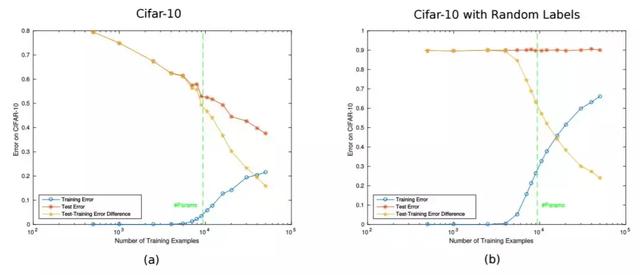
经典的学习理论将学习系统的泛化行为描述为训练样本数 n 的函数。从这个角度看，DNN 的行为和期望一致：更多训练数据带来更小的测试误差，如图 1a 所示。该学习曲线的其他方面似乎不够直观，但也很容易解释。例如即使在训练误差为零时，测试误差也会随着 n 的增加而减小（正如 [1] 中所指出的那样，因为被报告的是分类误差，而不是训练过程中被最小化的风险，如交叉熵）。看起来 DNN 展示出了泛化能力，从技术角度上可定义为：随着 n → ∞，训练误差收敛至期望误差。图 1 表明对于正常和随机标签，模型随 n 的增加的泛化能力变化。这与之前研究的结果一致（如 [8]），与 [9] 的稳定性结果尤其一致。注意泛化的这一特性并不寻常：很多算法（如 K 最近邻算法）并不具备该保证。

图 1：不同数量训练样本下的泛化。（a）在 CIFAR 数据集上的泛化误差。（b）在随机标签的 CIFAR 数据集上的泛化误差。该深度神经网络是通过最小化交叉熵损失训练的，并且是一个 5 层卷积网络（即没有池化），每个隐藏层有 16 个通道。ReLU 被用做层之间的非线性函数。最终的架构有大约 1 万个参数。图中每一个点使用批大小为 100 的 SGD 并训练 70 个 epoch 而得出，训练过程没有使用数据增强和正则化。

泛化的这一特性虽然重要，但在这里也只是学术上很重要。现在深度网络典型的过参数化真正难题（即本论文的重点）是在缺乏正则化的情况下出现明显缺乏过拟合的现象。从随机标注数据中获得零训练误差的同样网络（图 1b）很显然展示出了大容量，但并未展示出在不改变多层架构的情况下，每一层神经元数量增加时期望误差会有所增加（图 2a）。具体来说，当参数数量增加并超过训练集大小时，未经正则化的分类误差在测试集上的结果并未变差。

图 2：在 CIFAR-10 中的期望误差，横轴为神经元数量。该 DNN 与图 1 中的 DNN 一样。（a）期望误差与参数数量增加之间的相关性。（b）交叉熵风险与参数数量增加之间的相关性。期望风险中出现部分「过拟合」，尽管该指数损失函数的特点略微有些夸大。该过拟合很小，因为 SGD 收敛至每一层具备最小弗罗贝尼乌斯范数（Frobenius norm）的网络。因此，当参数数量增加时，这里的期望分类误差不会增加，因为分类误差比损失具备更强的鲁棒性（见附录 9）。

我们应该明确参数数量只是过参数化的粗略表征。实验设置详见第 6 章。

5 深度网络的非线性动态

5.3 主要问题

把所有引理合在一起，就得到了

定理 3：给定一个指数损失函数和非线性分割的训练数据，即对于训练集中的所有 x_n，∃f(W; x_n) 服从 y_n*f(W; x_n) > 0，获得零分类误差。以下特性展示了渐近平衡（asymptotic equilibrium）：
GD 引入的梯度流从拓扑学角度来看等于线性化流；
解是每一层权重矩阵的局部极小弗罗贝尼乌斯范数解。

在平方损失的情况下分析结果相同，但是由于线性化动态只在零初始条件下收敛至极小范数，因此该定理的最终表述「解是局部极小范数解」仅适用于线性网络，如核机器，而不适用于深度网络。因此在非线性的情况下，平方损失和指数损失之间的差别变得非常显著。对其原因的直观理解见图 3。对于全局零最小值附近的深度网络，平方损失的「地形图」通常有很多零特征值，且在很多方向上是平坦的。但是，对于交叉熵和其他指数损失而言，经验误差山谷有一个很小的向下的坡度，在||w||无限大时趋近于零（详见图 3）。

在补充材料中，研究者展示了通过惩罚项 λ 写出 W_k = ρ_k*V_k，并使 ||V_k||^2 = 1，来考虑相关动态，从而展示初始条件的独立性以及早停和正则化的等效性。

图 3：具备参数 w_1 和 w_2 的平方损失函数（左）。极小值具备一个退化 Hessian（特征值为零）。如文中所述，它表示在零最小值的小近邻区域的「一般」情况，零最小值具备很多零特征值，和针对非线性多层网络的 Hessian 的一些正特征值。收敛处的全局最小值附近的交叉熵风险图示如右图所示。随着||w|| → ∞，山谷坡度稍微向下。在多层网络中，损失函数可能表面是分形的，具备很多退化全局最小值，每个都类似于这里展示的两个最小值的多维度版本。

5.4 为什么分类比较不容易过拟合

由于这个解是线性化系统的极小范数解，因此我们期望，对于低噪声数据集，与交叉熵最小化相关的分类误差中几乎很少或没有过拟合。注意：交叉熵作为损失函数的情况中，梯度下降在线性分离数据上可收敛至局部极大间隔解（local max-margin solution），起点可以是任意点（原因是非零斜率，如图 3 所示）。因此，对于期望分类误差，过拟合可能根本就不会发生，如图 2 所示。通常相关损失中的过拟合很小，至少在几乎无噪声的数据情况下是这样，因为该解是局部极大间隔解，即围绕极小值的线性化系统的伪逆。近期结果（Corollary 2.1 in [10]）证明具备 RELU 激活函数的深度网络的 hinge-loss 的梯度最小值具备大的间隔，前提是数据是可分离的。这个结果与研究者将 [1] 中针对指数损失的结果扩展至非线性网络的结果一致。注意：目前本论文研究者没有对期望误差的性质做出任何声明。不同的零最小值可能具备不同的期望误差，尽管通常这在 SGD 的类似初始化场景中很少出现。本文研究者在另一篇论文中讨论了本文提出的方法或许可以预测与每个经验最小值相关的期望误差。

总之，本研究结果表明多层深度网络的行为在分类中类似于线性模型。更准确来说，在分类任务中，通过最小化指数损失，可确保全局最小值具备局部极大间隔。因此动态系统理论为非过拟合的核心问题提供了合理的解释，如图 2 所示。主要结果是：接近经验损失的零极小值，非线性流的解继承线性化流的极小范数特性，因为这些流拓扑共轭。损失中的过拟合可以通过正则化来显性（如通过权重衰减）或隐性（通过早停）地控制。分类误差中的过拟合可以被避免，这要取决于数据集类型，其中渐近解是与特定极小值相关的极大间隔解（对于交叉熵损失来说）。

6 实验

图 4：使用平方损失在特征空间中对线性网络进行训练和测试（即 y = WΦ(X)），退化 Hessian 如图 3 所示。目标函数是一个 sine 函数 f(x) = sin(2πfx)，在区间 [−1, 1] 上 frequency f = 4。训练数据点有 9 个，而测试数据点的数量是 100。第一对图中，特征矩阵 φ(X) 是多项式的，degree 为 39。第一对图中的数据点根据 Chebyshev 节点机制进行采样，以加速训练，使训练误差达到零。训练使用完整梯度下降进行，步长 0.2，进行了 10, 000, 000 次迭代。每 120, 000 次迭代后权重受到一定的扰动，每一次扰动后梯度下降被允许收敛至零训练误差（机器准确率的最高点）。通过使用均值 0 和标准差 0.45 增加高斯噪声，进而扰动权重。在第 5, 000, 000 次迭代时扰动停止。第二张图展示了权重的 L_2 范数。注意训练重复了 29 次，图中报告了平均训练和测试误差，以及权重的平均范数。第二对图中，特征矩阵 φ(X) 是多项式的，degree 为 30。训练使用完整梯度下降进行，步长 0.2，进行了 250, 000 次迭代。第四张图展示了权重的 L_2 范数。注意：训练重复了 30 次，图中报告了平均训练和测试误差，以及权重的平均范数。该实验中权重没有遭到扰动。

7 解决过拟合难题

本研究的分析结果显示深度网络与线性模型类似，尽管它们可能过拟合期望风险，但不经常过拟合低噪声数据集的分类误差。这遵循线性网络梯度下降的特性，即风险的隐性正则化和对应的分类间隔最大化。在深度网络的实际应用中，通常会添加显性正则化（如权重衰减）和其他正则化技术（如虚拟算例），而且这通常是有益的，虽然并非必要，尤其是在分类任务中。

如前所述，平方损失与指数损失不同。在平方损失情况中，具备任意小的 λ 的正则化（没有噪声的情况下）保留梯度系统的双曲率，以收敛至解。但是，解的范数依赖于轨迹，且无法确保一定会是线性化引入的参数中的局部极小范数解（在非线性网络中）。在没有正则化的情况下，可确保线性网络（而不是深度非线性网络）收敛至极小范数解。在指数损失线性网络和非线性网络的情况下，可获得双曲梯度流。因此可确保该解是不依赖初始条件的极大间隔解。对于线性网络（包括核机器），存在一个极大间隔解。在深度非线性网络中，存在多个极大间隔解，每个对应一个全局最小值。在某种程度上来说，本研究的分析结果显示了正则化主要提供了动态系统的双曲率。在条件良好的线性系统中，即使 λ → 0，这种结果也是对的，因此内插核机器的通用情况是在无噪声数据情况下无需正则化（即条件数依赖于 x 数据的分割，因此 y 标签与噪声无关，详见 [19]）。在深度网络中，也会出现这种情况，不过只适用于指数损失，而非平方损失。

结论就是深度学习没什么神奇，在泛化方面深度学习需要的理论与经典线性网络没什么不同，泛化本身指收敛至期望误差，尤其是在过参数化时出现了过拟合缺失的情况。本研究分析通过将线性网络的特性（如 [1] 强调的那些）应用到深度网络，解释了深度网络泛化方面的难题，即不会过拟合期望分类误差。

8 讨论

当然，构建对深度网络性能有用的量化边界仍然是一个开放性问题，因为它是非常常见的情形，即使是对于简单的仅包含一个隐藏层的网络，如 SVM。本论文研究者主要的成果是图 2 所展示的令人费解的行为可以通过经典理论得到定性解释。

该领域存在很多开放性问题。尽管本文解释了过拟合的缺失，即期望误差对参数数量增加的容错，但是本文并未解释为什么深度网络泛化得这么好。也就是说，本论文解释了为什么在参数数量增加并超过训练数据数量时，图 2 中的测试分类误差没有变差，但没有解释为什么测试误差这么低。

基于 [20]、[18]、[16]、[10]，研究者猜测该问题的答案包含在以下深度学习理论框架内：
不同于浅层网络，深度网络能逼近层级局部函数类，且不招致维数灾难（[21, 20]）。
经由 SGD 选择，过参数化的深度网络有很大概率会产生很多全局退化，或者大部分退化，以及「平滑」极小值（[16]）。
过参数化，可能会产生预期风险的过拟合。因为梯度下降方法获得的间隔最大化，过参数化也能避免过拟合低噪声数据集的分类误差。

根据这一框架，浅层网络与深度网络之间的主要区别在于，基于特定任务的组织结构，两种网络从数据中学习较好表征的能力，或者说是逼近能力。不同于浅层网络，深度局部网络特别是卷积网络，能够避免逼近层级局部合成函数类时的维度灾难（curse of dimensionality）。这意味着对于这类函数，深度局部网络可以表征一种适当的假设类，其允许可实现的设置，即以最小容量实现零逼近误差。

论文：Theory IIIb: Generalization in Deep Networks

论文链接：https://arxiv.org/abs/1806.11379

摘要：深度神经网络（DNN）的主要问题围绕着「过拟合」的明显缺失，本论文将其定义如下：当神经元数量或梯度下降迭代次数增加时期望误差却没有变差。鉴于 DNN 拟合随机标注数据的大容量和显性正则化的缺失，这实在令人惊讶。近期 Srebro 等人的研究结果为二分类线性网络中的该问题提供了解决方案。他们证明损失函数（如 logistic、交叉熵和指数损失）最小化可在线性分离数据集上渐进、「缓慢」地收敛到最大间隔解，而不管初始条件如何。本论文中我们证明了对于非线性多层 DNN 在经验损失最小值接近零的情况下也有类似的结果。指数损失的结果也是如此，不过不适用于平方损失。具体来说，我们证明深度网络每一层的权重矩阵可收敛至极小范数解，达到比例因子（在独立案例下）。我们对动态系统的分析对应多层网络的梯度下降，这展示了一种对经验损失的不同零最小值泛化性能的简单排序标准。
,