等腰直角三角形几何题解题方法（这道题涉及等腰直角三角形）

各位朋友，大家好！今天是2020年9月20日星期日，数学世界将继续为大家分享小学五、六年级的数学竞赛试题以及高年级的数学思考题。今天我们讲解一道有关等腰直角三角形的面积计算的数学思考题，此题属于能力拓展题。

对于大多数学生来说还是有一定难度，但是只要掌握了等腰直角三角形的面积求法，学生应该能够理解这样的解题思路。数学世界在此分享这些有趣的数学题，目的是希望能够激发学生学习数学的兴趣，并且能够给大家的学习提供一些帮助！

例题：（小学数学思考题）如图，有两块等腰直角三角形的三角板，直角边分别是10厘米和6厘米，把它们按照图中那样重合，求重合部分（阴影部分）的面积是多少平方厘米？

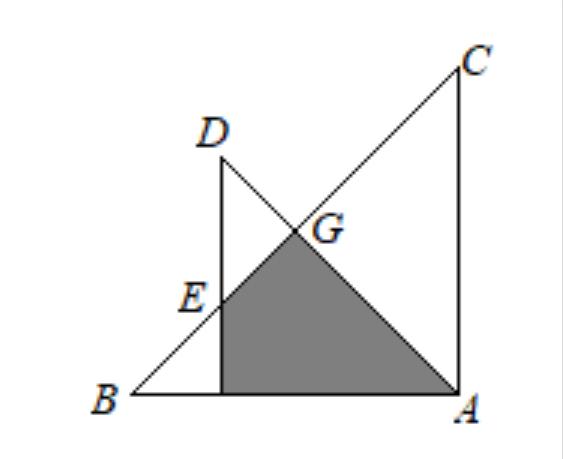
这道题要求的是阴影部分的面积，显然这重合部分并不是一个规则图形，只能通过相关图形面积相加减求出。其实这道题并不是很难，对于成绩较好的同学完全能够做出来，但是还有很多学生看完题目后，不知如何从哪里进行思考，根本做不出来。对于这样的数学题，需要较强的观察和分析能力。接下来，数学世界就与大家一起来完成这道例题吧！

分析：仔细观察图形后，分析可知：阴影部分的面积=三角形ABG的面积-三角形BEF的面积。于是只要求出这两个三角形的面积，问题就解决了。先来求三角形ABG的面积，由于三角形ABC和三角形ADF都是等腰直角三角形，所以可以推出三角形ABG和三角形ACG也是等腰直角三角形，于是BG=GC，所以三角形ABG的面积等于三角形ABC面积的一半，而三角形ABC的面积容易求出。

下面，我们再来求三角形BEF的面积，根据题意，三角形BEF也是等腰直角三角形，直角边BF=AB-AF=10-6=4厘米，于是三角形BEF的面积容易求出。由此列式解答即可，于是问题就可以得到解决。下面，我们就按照以上思路解答此题吧！

解答：经过分析可知：

阴影部分的面积=三角形ABG的面积-三角形BEF的面积。

由于三角形ABC和三角形ADF都是等腰直角三角形，

所以∠B=∠C=∠BAG=∠CAG=45°，

即三角形ABG和三角形ACG也是等腰直角三角形，

可以得出BG=GC，

因此，三角形ABG的面积等于三角形ABC面积的一半，

因为三角形ABG的直角边分别是10厘米，

三角形ABG的面积为：

10×10÷2÷2=25（平方厘米）

根据题意，三角形BEF也是等腰直角三角形，

直角边BF=AB-AF=10-6=4（厘米）

三角形BEF的面积为：

4×4÷2=8（平方厘米）

所以阴影部分的面积为：

25-8=17（平方厘米）

答：阴影部分的面积是17平方厘米。

（完毕）

这道题主要考查了等腰直角三角形的性质和面积计算。解答此题的关键是：通过仔细观察图形，找出阴影部分面积的计算方法，求三角形ABG的面积是此题的难点。温馨提示：朋友们如果有不明白之处或者有更好的解题方法，欢迎大家在下面留言讨论。