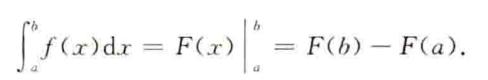考研数学积分怎么计算（定积分计算体系要点详谈）

1. 基本方法
2. 基本性质
3. 基本结论与技巧
4. 基本题型（每个类型的特征 解题要点）
5. 如何用好题型问题简单谈谈。

• 本次文稿仅作为梳理问题，基于不定积分计算的前提下，希望能给人以帮助，在这一部分就统考的数学而言，个人建议可以借助题型分类，从而可以根据不同类型的题干本身的特征，快速定位题型，进而锁定方法方向，更有针对性解决问题。

要想定积分计算的快，准，易，除不定积分基础外，应当把该背的公式和方法梳理清楚。

定积分计算体系

• 2.1 牛顿莱布尼茨公式

图片-02 牛顿莱布尼茨公式

前提条件请自己查。本来原函数存在，与定积分是否存在，但牛顿莱布尼茨公式建立起了两者的关系，给出了：用原函数求定积分的方法。 因此，不定积分计算必然是基础。

• 公式两步走：1.算原函数（不定积分）；2.代上下限
• 2.2 定积分的换元法（注意条件，涉及到个别题开根号之后取值正负）

图-03 摘选自《复习指南》

定积分换元法(3换步骤）： 1.换元 x=g(t)；2.换微元：dx=dg(t)=g'(t)dt； 3.换上下限：x=a，则t=m;x=b,则t=n[一一对应]

• 相比不定积分换元法而言，定积分换元不需要回代，只用把对应的上下限值改掉即可。

图-04 摘选自《同济教材高数》

• 简化定积分换元手法：先凑微分，再平衡系数，将来换微元的时候就不用求导了。

图-05 简化定积分换元的一个手法

• 2.3 定积分的分布积分法

图-06 分部积分法

07-基本性质

08-基本性质

结论：定积分的值只与积分区间，被积分函数有关，与其积分变量x的记号无关，当被积分函数仅含积分变量，且上下限为常数的时候，其值为一个数K.

09-会识别是个数

此类题的解题要点：识别定积分=K，两边积分构造A=K BA的等式进而解出A。

基本结论与技巧（背多分）

1.定积分的几何意义（借用熟悉的平面图形的面积来求解）

易错点：定积分与面积的概念是有区别的，经过实测2019考研数学真题求围绕面积的那个大题很多同学上来写错了表达式，甚至看了答案后还不知为何套了绝对值。实则基本概念出现了问题，因此要重视基本概念，定理和结论的前提条件。

10-来自百度文库某位老师的PPT

11-常用定积分几何意义公式

2.对称区间上的积分性质：

要点：1.先看整体以及局部是否具有奇偶对称性，有就用相应的结论 ; 2.没有则转化到正区间看“f(x) f(-x)” 设其中g(x)=f(x) f(-x)→先看是否能约分化简；否则再拿去g(x)求导看导数是否为0，若导数为0，则恒为常数g(x)=g(0)(找特殊点）≡K（算常数） 通常考研数学的题，这个点一般会是提出一部分因子，剩余部分要么能化简约分；要么恒为常数找个特殊点算出来；当然再往深一步，就是分部积分法抵消一部分。

12-摘选某书

13-典型例题

3.周期函数，三角函数的基本公式与结论

周期函数

• 华里士公式你会熟练用吗？此外后期的伽马函数你也会灵活用吗？

华里士公式

上述结论要求会证会用，要敏感，证明见同济教材定积分换元部分例题，这一节的例题都是典型例题。

4.要灵活运用分项积分与结合积分，分部积分法

小技巧

基本题型分类（关注：分类的特征 解题要点 ）

题型1：基本型：属于大众脸，不特殊的常规性。

识别特征：如何识别呢？排除【下文】特殊几个典型题型，剩余的就是它-基本型。 解题要点： 方向→牛顿莱布尼茨公式， 算原函数，代上下值 方法→凑微分，换元法，分部积分法 前提：不定积分中常见的换元结构要记住。根式etc

牛顿莱布尼茨公式

偶尔可能需要先处理下求出表达式，（符号的运用，整体代换）

例题

题型2：对称区间类型

典型特征：区间上下限相反数对称→1s就可以识别出来了吧。 解题要点：见前文基本结论部分，

对称区间

题型3：分段函数，|*|，max min，sign

典型特征:形如这类分段函数的特征，我想题干表达式很鲜明的特征，你肯定会识别。 解题要点:形如∫f(g(t))dt,先做变量替换u=g(t)化简，然后从分段点拆分，分段积分。

分段函数

题型4：被积分函数含变限积分函数，且无法积分出来的 或者 被积分函数含有导数类型

要点：借助分部积分法，可对阶数进行升降处理。

类型一：被积分函数含变限积分函数，且无法积分出来.

识别特征：1.被积分函数含有变限积分函数；2.所含变限积分函数不可积分出；

解题要点：分部积分法&二重积分换序【理着口诀换序即可】

能识别出的前提：被积函数，变限积分函数要知道；不可积分函数要积累一些有重要用途。

【注意】是不可积分出来的变限积分函数才用分部或者二重积分换序，能积分出来就算呗。

【题外之话】：部分同学因为改了字母，就不会识别这类型可以看作为二重积分(请查概念) ∫dx∫f(x,y)dy=∫[∫f(x,y)dy]dx,倒着看:要会把先积分部分视为一元中的被积函数.

【重要】分部积分法的要点：先凑变限积分函数之外部分的微分，再用一次分部积分定理，就能把不可积分出来的变限积分函数求导干掉了。（好好看这句话，解题的关键）

仔细看看

常见不可积分的函数有哪些，它们有什么作用呢？ 1.在一元积分中出现，由于不可积分，因此暗示你分部积分处理； 2.在二重积分先积分部分出现，由于不可积分，暗示你调换二重积分次序； 亦可：先设不可积分部分为G(x)。 3.以上两种途径均不可解决，那么你放心，必然是题中有相互抵消的部分。

常见不可积分的函数积累

类型二：被积分函数含有导数→方向：分部积分法

典型特征：被积分函数含有导数的定积分 解题要点：分部积分法→把导数部分先凑微分 与上一类题恰好相反。

典型例题

题型5：含周期函数，三角函数是天生的周期函数，别看见三角函数没有冲动，以及结论。

• 典型特征：周期函数，三角函数 sinx cosx
• 解题要点：用好有关的基本结论见前文，取好a=?（证明过程值得借鉴）

周期，三角函数的若干结论

题型6:区间再现型：几乎是超纲的，记住几个典型的。（考的概率很低，了解即可）

特别的∫x|sinx|dx这种再现值得借鉴上述公式的证明。 【心得】：但凡你尝试了其他方法解决不出来的时候，进行不下去，往往就是利用换元法，区间再现来求解。

常见区间再现

题型7.大题考点，含参数积分的定积分。如何讨论，特别是绝对值类型，如何优雅的去绝对值(2次大题)

请详看下图含参数绝对值的定积分，如何分段处理的解决办法。

绝对值

如何用好题型分类？

• 观点：任何时候基本概念，基本定理和基本方法，基本计算是基础和重点。题型只是辅助梳理。
• 当然数学应试就避免不了题型的训练，并且部分经典命题模式已经固定，由此梳理常考的符合命题依据的科学分类的题型解题要点，程序有时候能提升解题速度。

很多人用不好题型的原因，是基于以下几个方面。

1.本来是题型课，可是你们自己做题的时候不会识别，反应不出来是课中那种题型。

2.对应的这类题的解题要点没梳理清楚，就算知道是这个题型，脑子里不知道分几步解，每一步做什么，怎么解，

3.怎么解，是需要相应的基本概念，基本定理和基本方法，以及扎实的基本计算作为依据的。（这里有问题也没办法）

4.独立，刻意重复练习太少，习惯看而不是动笔，过于沉迷视频等。缺乏大量的练习和总结。

• 两个情景的启发：

场景

要用好题型的前提，首先相应的基本功扎实，其次对题型的解题要点要梳理清楚，明确这类题的解题方向和步骤，知道这个题从那个角度切入，分几步解，每一步做什么怎么做。但是这个还得基于一个前提：就是你要能从茫茫题海中识别出这个题是属于见过的那种题型，场景问题中所说M国的人具有肤色的特征特点，其实题型分类往往基于题干条件的一些差别特点，比如对称区间，被积分函数含有变限积分，这些特征我想你只需要1S就能识别出来了吧。考场没有提示，因此平时需要关注这些特征，从那个特征看出来用那个方法，怎么做到“什么时候用什么方法”。微分方程中按类型求解，在此给你把定积分计算也按类型求解，你只要拿到一个定积分计算题，锁定对应的特征，然后根据上文梳理的解题要点去操作，基本考研数学的题是能完美搞定的。

• 举个栗子：

真题训练

• 本来这套体系应该结合我借助一些例题具体的讲解如何使用，那样的话更容易吸收。但是上文已经给了例题展示，目前也没有时间做视频分享。自己琢磨。
• 考研数学一个典型的东西：特征→（定位了类型）→决定：方法
• 并非所有的题型分类都靠谱，只是辅助梳理。关键是梳理清楚思维，个人觉得定积分计算部分可以采用题型分类来学习。上述题型分类和要点，只要你借助一定的题目来训练，我想你可以复制思维，1s钟之内就可以识别出那一种题型，是从而反应出解题的方向。因为特征太明显了。

本文档直接借助了部分资料的截图，再次表示歉意，由于没太多时间来键入公式与文字，但不做任何商业用途，单纯分享，望能理解。

谢谢收看本期节目。

,