狭义相对论的相对速度公式推导（顺手推导狭义相对论公式）

南阳师范学院 左军超

1、 三维空间和四维时空

在三维空间中，最大的特点是两个点的距离不随坐标系的变换也而变化。你无论是平移还是旋转，两个点的距离r始终是一个定值。如果设一个坐标为原点，则r=(x^2 y^2 z^2)^（1/2）是一个定值，S=x^2 y^2 z^2为一个定值。

但是在四维时空下，x^2 y^2 z^2不再是一个定值，加入时间这个坐标后，S= x^2 y^2 z^2-(ct)^2才是一个定值，亦可以表示为S=r^2-(ct)^2为一个定值，或者S= x^2 y^2 z^2 (ict)^2。其中i是虚数，i^2=-1。

这样，在四维时空中根据S是一个定值，很容易推导出v=dr/dt=c，或者vx=dx/dt=c(假设沿x方向运动)。

也就是说，在四维时空中，没有静止质量的玻色子，在不与任何其它物质产生相互作用的真空中，其速度为c是一个天然属性，是由四维时空的自身性质决定的。

这样，原来三维空间中的三个相互垂直的坐标系x轴、y轴和z轴在四维的时空坐标中，则由x轴、y轴、z轴和ict轴（简写为w轴）代替。任何一点在时空中的坐标位置，都可以有x，y，z和ict(w)四个坐标来表示。

为了表示直观，我们舍去y轴和z轴，仅展示出x轴和w轴，并顺手推导出看似神奇的狭义相对论坐标转换公式。

2、 狭义相对论公式的推导

如图所示，如果假设我们自身为原点，且静止不动，则我们自身在时空坐标中的状态是什么？是一条沿w坐标轴向上的直线，x坐标值始终为0，而时间t在流逝，ict值在不断增加。

此时，如果有一个物体相对于我们沿着x轴正向以速度v运动，那么它在时空坐标中的状态是什么呢？是一条斜直线，如图所示，如果其x坐标表示为vt，则其w坐标为ict，其与w坐标轴的夹角θ。很容易得出tanθ=-iv/c，并可以顺手推出sinθ=-

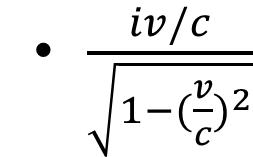
，cosθ=

。

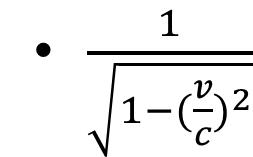
如果现在我们以该运动物体为参照系，意味着什么？就意味着该物体的运动状态变成了新的w轴，我们设为w'。此时我们就有了一个新的坐标系w'、x'。

那如果原来的坐标系中有一点S（x,ict），其在新的坐标系中的，其坐标值(x',ict')是什么呢？

根于w'轴相对于w轴的位置可以看出，坐标轴绕原点顺时针旋转了θ角，也就相当于坐标相对于原点逆时针旋转了θ。根据坐标变化公式，x'=xcosθ-wsinθ，w'=xsinθ wcosθ，将sinθ和cosθ的值带入，即可得

，

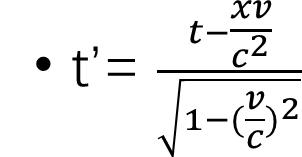
这恰好就是狭义相对论的坐标转换公式。

如果仔细看完这个推导过程，就可以看出其实这个推导非常简单，是四维时空坐标系下一个顺手完成的事情。唯一需要注意的是时间轴的坐标是一个虚坐标，处理的时候要小心一点。

狭义相对论的时空坐标转换公式不神奇，真正有意思的是对四维时空的理解，这才是更有价值和意义，也更有趣的事情，对于我们理解量子力学中费米子和玻色子的运动属性，可以起到非常重要的作用。