拉马努金为什么不能自己证明公式 颠覆你认知的π

我们都知道圆周率π，一开始人们是利用割圆术逐渐逼近的方法来计算π。我国古代著名数学家祖冲之就曾利用割圆术将π精确计算到小数点后7位。

π=3.1415926……

但这种计算方法的逼近速度太慢，在那个没有计算机的时代，要想准确计算π非常困难。荷兰数学家鲁道夫曾将π精确计算到小数点后35位，人们为了纪念他，将这个35位小数命名为“鲁道夫数”，并刻在了鲁道夫的墓碑上。

随着数学体系的发展，人们逐渐发现了π的多种表达方式和逼近公式。今天我们首先来介绍一个非常著名的表示π的级数——莱布尼茨级数。

我们一步步慢慢来，先求出反正切函数y=arctan(x)的导数。

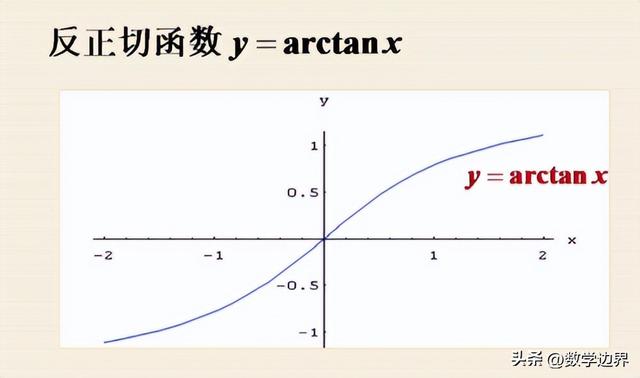
求：y′(x)=arctan′(x)

解：y=arctan(x)，x=tan(y)

dx/dy=d[tan(y)]/dy=tan′(y)

=[sec(y)]^2=1 [tan(y)]^2=1 x^2

y′(x)=dy/dx=1/(dx/dy)=1/(1 x^2)

arctan′(x)=1/(1 x^2)

利用麦克劳林公式可将1/(1 x^2)作如下展开：

麦克劳林公式

1/(1 x^2)=1-x^2 x^4-x^6 …

这里展开过程从略，留给大家自行验证。

由arctan′(x)=1/(1 x^2)，可得

∫[1/(1 x^2)]=arctan(x)

由[x^(n 1)]′=(n 1)x^n，可得

[x^(n 1)/(n 1)]′=x^n

∫(x^n)=x^(n 1)/(n 1)

对以上等式两边同时积分

∫[1/(1 x^2)]=∫(1-x^2 x^4-…)

arctan(x)=x-x^3/3 x^5/5-…

由tan(π/4)=1，可得arctan(1)=π/4

对以上等式，令x=1

arctan(1)=1-1^3/3 1^5/5-…

我们得到了著名的莱布尼兹级数：

π/4=1-1/3 1/5-1/7 …

这个形式真是太美妙了，真是令人陶醉。

莱布尼茨级数

对莱布尼兹级数两边同乘以4，就得到了π的另一种表达式：

π=4×(1-1/3 1/5-1/7 …)

利用莱布尼兹级数来逼近π，显然比割圆术提升了一个维度。

然而，人们逐渐发现，莱布尼兹级数的收敛速度还是太慢了。英国数学梅钦受莱布尼兹级数的启发，提出了收敛速度更快的梅钦公式。

π/4=4arctan(1/5)-arctan(1/239)

梅钦公式

注意：梅钦公式并不是一个无穷级数，也不是一个近似公式，而是一个完全精确计算π的有限项等式。

如果你是第一次看到这个公式，你一定会惊讶于公式中出现的常数“239”，这个数是怎么出现的？这个数怎么可能精确计算π？

接下来我就严格证明梅钦公式，真正让你心服口服。

求证：

π/4=4arctan(1/5)-arctan(1/239)

证明：令tan(x)=1/5

根据二倍角公式

tan(2x)=2tan(x)/{1-[tan(x)]^2}

=2×(1/5)/[1-(1/5)^2]

=(2/5)/(24/25)=5/12

tan(4x)=tan(2×2x)

=2×(5/12)/[1-(5/12)^2]

=(5/6)/(119/144)=120/119

根据两角和差公式

tan(4x-π/4)

=(120/119-1)/[1 (120/119)×1]

=(120-119)/(119 120)=1/239

tan(4x-π/4)=1/239

4x-π/4=arctan(1/239)

π/4=4x-arctan(1/239)

=4arctan(1/5)-arctan(1/239)

π/4=4arctan(1/5)-arctan(1/239)

证毕！

利用前面推导的arctan(x)的展开式去计算：

arctan(1/5)和arctan(1/239)

arctan(x)=x-x^3/3 x^5/5-…

在那个没有计算器的年代，可以轻松将π计算到小数点后100多位，这是多么可怕的成就。是多么惊人的想象力才能创造出这样一个公式，就问你服气不服气。

然而，真正令人恐怖的人物即将出现。如果说人类历史上只有一位绝世数学天才的话，那这个人只能是拉马努金，在娜玛卡尔女神的指引下，拉马努金已然是那个最接近神的男人。

拉马努金

拉马努金说道，在我眼里梅钦公式的收敛速度实在是太缓慢了，于是他一挥手写下了震惊世人的拉马努金公式。

拉马努金公式

当我第一次看到这个公式时，内心的震惊无以言表，完全颠覆了我对数学公式的认知。拉马努金公式的出现让人类感受到了被神支配的恐惧，这是人类能够构造出来的公式吗？

拉马努金给公式几乎不给证明过程，只有结论。拉马努金一生创造了2000多个诸如此类的公式，这些公式大多都是灵光乍现写出来的，没有留下证明过程。后人通过反复研究拉马努金留下的宝贵遗产，已证得他留下的众多没有严格证明的结论中，几乎都是正确的。

“不要问我公式里面那些26390等常数是怎么来的，我只能告诉你那是娜玛卡尔女神在梦中指引我。”

1985年，人们第一次利用计算机对拉马努金公式进行计算，第一次出手就将π计算到了小数点后1700万位，开创了前无古人的新高度，这简直就是对莱布尼兹级数和梅钦公式的降维打击。

,