数学二次函数例题（数学第二章函数）

1. 二次函数：一般地，自变量x和因变量y之间存在如下关系：一般式：

则称y为x的二次函数。

2.二次函数的解析式三种形式。

一般式

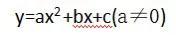
顶点式

交点式

3.二次函数图像与性质

对称轴

顶点坐标

与y轴交点坐标（0，c）

4.增减性：

当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大

当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小

5.二次函数图像画法：

勾画草图关键点：1开口方向 2对称轴 3顶点 4与x轴交点 5与y轴交点

6.图像平移步骤

（1）配方

确定顶点（h,k）

（2）对x轴 左加右减；对y轴 上加下减

7.二次函数的对称性

二次函数是轴对称图形，有一结论：横坐标为x1, x2 其对应纵坐标相等则对称轴

8.根据图像判断a,b,c的符号

（1）a ——开口方向

（2）b ——对称轴与a 左同右异

9.二次函数与一元二次方程的关系

抛物线

与x轴交点的横坐标x1, x2 是一元二次方程的根

抛物线

当y=0时，抛物线便转化为一元二次方程

当

时，一元二次方程有两个不相等的实根，二次函数图像与x轴有两个交点；

当

时，一元二次方程有两个相等的实根，二次函数图像与x轴有一个交点；

当

时，一元二次方程有不等的实根，二次函数图像与x轴没有交点

需要免费的数学专业指导，请私信我。

,