路径最短的几何问题（数学模型下的航线较短）

问题：

从北京（靠近北纬40°、东经120°，以下经纬度均取近似值）飞往南非首都约翰内斯堡（南纬30°、东经30°），有两条航空线可供选择：

甲航空线：从北京沿纬度弧向西飞到土耳其首都安卡拉（北纬40°、东经30°），然后向南飞到目的地；

乙航空线：从北京向南飞到澳大利亚的珀斯（南纬30°、东经120°），然后向西飞到目的地．

请问：哪一条航空线较短（地球视为半径R=6370km的球）？

解：把北京、约翰内斯堡、安卡拉、珀斯分别看作球面上的A、B、C、D四点（如图），则甲航程为A、C两地间的纬度长⌒AC与C、B两地间的球面距离⌒BC之和，乙航程是A、D两地间的球面距离⌒AD加上D、B两地间的纬度线长⌒DB．

设球心为O， O1、O2分别是北纬40°圆与南纬30°圆的圆心，则

从而，

．

故甲航程为:

乙航程为:

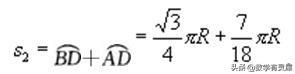
由cos40°<cos30°，知S1<S2，，所以甲航空线较短．

今天的分享结束，欢迎留言、收藏、分享、关注！