四下数学三角形三边的关系讲解（小学数学中三角形三边关系学习的四次思维转折）

　　小学数学中三角形三边关系学习的四次思维转折

　　2018年8月25日星期六

　　这部分内容来源于人教2011版小学四年级《数学》下册第五单元“三角形”，该单元带领小朋友们学习了三角形的特性、三角形的分类、三角形的内角和。其中三角形的特性一节的内容具体又有：三角形的概念、表示、底和高、稳定性、三边关系。在这些“特性”中：“概念和表示”是最基础的，也是学习起来最自然的，三角形有3个顶点、3条边、3个角，命名抓住了“3个顶点”，比如：三角形ABC（大写字母表示点的名称，小写字母表示线的名称，这是一种数学字母符号表示的约定俗成），概念则抓住了“3条线段”围成的图形，可见，最基本的性质都和数字“3”相关；“底和高”的学习除了理解概念，还要重视操作，二者不可偏颇，相互促进；“稳定性”的理解可简单可深入，简单来说：三角形木框区别于长方形木框“拉不动”三字，即可构成对“三角形具有稳定性”最直观的理解，深入地谈则有：形状的唯一性、形状的不变性以及边数大于3的多边形“容易变形”的特点，是一块在理解上“弹性”很大的内容；考虑到小学生学习、计算、应试的实际，综合对比：“三边关系”的学习难度最大，理解层次多，解答题型丰富，考试比重大，故而本文择其谈之。对于“稳定性”，似乎也有谈谈的必要，后续再看情况。

　　教材关于三角形“三边关系”的学习只提供了1页内容2个例子，见下图：

人教版四年级数学下册63页

　　从这些内容来看，三角形三边关系的学习根本不需要“四次”思维转折，只需“两次”就够了。但从学生面对的试题、配练实际出发，要求被“拔高”了。因此，本文的视角基于教材，统筹练习，面向小朋友们的学习实际。

　　第一次思维转折：理解公理，应用公理。

　　此处所说的“公理”，即例3所要表达的内容，如下图：

　　这条“公理”概括起来叫做“两点之间线段最短”。何谓“公理”？即公认的道理。即是公认，便是勿需证明的基本的正确事实，这些“公理”往往构成了一门学科的出发点。值得一提的是，我们初中所学的《几何》其实完整点应当叫做《欧几里得几何》：“欧几里得几何指按照古希腊数学家欧几里得（公元前330年～公元前275年）的《几何原本》构造的几何学。欧几里得几何有时单指平面上的几何，即平面几何。三维空间的欧几里得几何通常叫做立体几何。高维的情形请参看欧几里得空间。”这是“百度百科”关于“欧氏几何”的简介，我借用一下。欧几里得几何有个主要的特点是：基于5条公理和定义，演绎出了诸多的定理和推论，构成了一套严密的“演绎系统”。这5条公理是：

　　“

　　1.过相异两点，能作且只能作一直线（直线公理）；

　　2.线段（有限直线）可以任意地延长；

　　3.以任一点为圆心、任意长为半径，可作一圆（圆公理）；

　　4.凡是直角都相等（角公理）；

　　5.两直线被第三条直线所截，如果同侧两内角和小于两个直角，则两直线作延长时在此侧会相交。

　　上述前三条公理是尺规作图公理，用来定直线与圆。第四条公理比较不一样，它好像是一个未证明的定理。事实上，它宣称着：直角的不变性或空间的齐性。它规范了直角，为第五公理铺路。第五公理又叫做平行公理，因为它等价于：

　　在一平面内，过直线外一点，可作且只可作一直线跟此直线平行。

　　”

欧几里得和《几何原本》

　　您也许会奇怪，这5条公理并不包含“两点之间线段最短”，这也是我的疑惑。我想要表达的是：

　　①我偶然间发现的问题“两点之间线段最短是公理吗”，并不是一个轻松的问题。从我的学习经历来看，我的几何老师确定无疑地讲给我们它是公理，网搜也可以得到大量“是公理”的答案。但是，也有不认为其是公理的，理由是“两点之间线段最短”是可以用“变分法”证明的。对此，我只能说：“水平有限，难以理解”。

　　②公理作为一门学科的基本出发点，往往决定了学科的发展方向。事实上，后来的数学家，比如高斯等人，改变了第5公理，发展起了全新的、高深莫测的“非欧几何”。这五大公理，原来是叫做5大公设的。即是假设，自然是可以改变的。但关于“公理”与“公设”的差别，细究起来，又是长篇累牍，只好作罢。

　　③对于解决问题的依据，寻根溯源，找出最初始的依据，是一种科学的态度。从小学数学教材的编排来看，自然也是以“两点之间线段最短”作为公理的。

　　……

　　就让我们逃开这些理论上的难题，转而关注于“两点之间线段最短”的本身意义，这才是小朋友们最应该直接面对的。

　　我想这句话可以啰嗦一点去理解：“两点之间，非线段比线段长”。有哪些“非线段”？譬如：折线、弧线、任意曲线。如下图：

折线

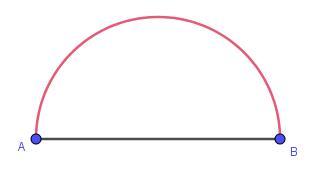
半圆弧

任意曲线

　　直观来看，确实“线段最短”。“直来直去，省时省力”，呵呵。

　　我们拿出“折了1次”的折线来对比：

1次折线

　　显然：红色的“一次折线”比黑色的线段长。由于整个图形构成了一个三角形，因而这个结论可以换个等价的说法：三角形两边之和大于第三边。于是，我们得出了三角形三边关系的最初的结论。

　　第二次思维转折：理解“任意”，拓展结论。

　　我们可以这样约定俗成地表示一个三角形：

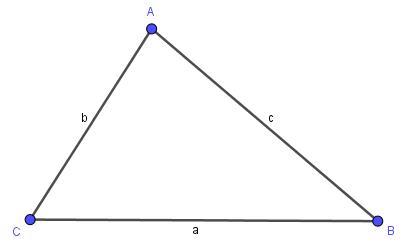
　　即三角形ABC，或△ABC，三个顶点为：A、B、C；三条边为：线段AB或c、线段BC或a、线段AC或b；三个角为：角A或∠A、角B或∠B、角C或∠C。以小写字母命名边时，遵循了：∠A的对边为a、∠B的对边为b、∠C的对边为c。

　　上述“思维转折一”事实上是以边AB为出发点观测，可得结论： BC＋AC＞AB，即：a＋b＞c。

　　“任意”的意思是可遍历或随意选取三角形的任一边为观测出发点：

　　以边BC为出发点观测，可得结论：AC＋AB＞BC，即：b＋c＞a；

　　以边AC为出发点观测，可得结论：BC＋AB＞AC，即：a＋c＞b。

　　于是，综合得出结论：

　　三角形任意两边的和大于第三边。

　　或表达为：第三边＜两边和

　　（重要程度★★★★）

　　此时，教材上的内容似乎完成了，只需再学习一些解题的技巧，比如下面的题：

人教版四年级数学下册练习十五第7题

　　以长3cm、4cm、5cm的小棒是否能拼成三角形为例说明：

　　完整的判断如下：

　　由于：

　　3＋4＞5成立

　　3＋5＞4成立

　　4＋5＞3成立

　　所以：长3cm、4cm、5cm的小棒能拼成三角形。

　　但事实上可以简化判断过程如下：

　　设任意给定三条线段为：a、b、c，且满足：a≤b≤c（实为对三条线段从短到长排序），如果有：a＋b＞c成立，则线段a、b、c一定能围成三角形。

　　用“不太准确的人话”描述就是：

　　只需检验：

　　小边＋中边＞长边，是否成立？

　　即可。

　　（重要程度★★★★）

　　这使得验证工作量“由3次降为1次”，对于解题，还是很实用的。比如：（5，6，11）不能围成三角形，原因只是：5＋6＞11不成立。

　　第三次思维转折：变“和”为“差”，转换角度。

　　已知三角形ABC，三条边为：a、b、c，我们已知的三边关系有：

　　a＋b＞c、a＋c＞b、b＋c＞a。

　　如果我们学习了“不等式的性质”，比如：

　　a＋b＞c

　　两边同时减去b，不等号的方向不变。

　　a＋b－b＞c－b

　　得：a＞c－b

　　也即：c－b＜a

　　同理有：c－a＜b 、b－c＜a、b－a＜c、a－b＜c、a－c＜b。

　　可得结论：

　　三角形任意两边的差小于第三边。

　　或表达为：两边差＜第三边

　　（重要程度★★★★）

　　但是，可惜的是，小学生并没有学习这些，我们需要转换思路：

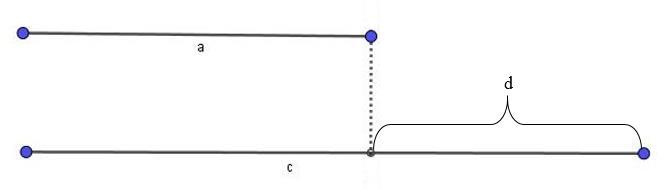
　　如上图，已知两条线段a、c，且a＜c，c－a＝d，此时如果要选择第三条线段b与线段a、c围成三角形，则线段b至少要比d长，否则根本“够不到”，因此有：

　　b＞d

　　即：b＞c－a

　　或许，这是唯一可以让小学生理解这个结论的办法。

　　第四次思维转折：“和”“差”对照，完善结论。

　　任意给定两条线段：a、b。请注意，此时我们是“完全任性”的，这两条线段的长度随意。

　　如果我们要接着给出第三条线段c，且a、b、c要能够围成三角形，则这个“第三边”便不能再“完全任性”了，在一定范围内，它才是自由的。即：第三边不能太长，要小于已知两边之和；第三边不能太短，要大于已知两边之差（自然选正值之差，或曰：绝对值大的差，小朋友对此忽略）。描述为：

　　两边差＜第三边＜两边和

　　（重要程度★★★★★）

　　例　已知一个三角形的两条边长为5cm、9cm，请问第三条边的长度可能是哪些？（仅罗列整厘米结果）

　　解：两边差＜第三边＜两边和

　　　　　9－5＜第三边＜9＋5

　　　　　　　4＜第三边＜14

　　答：第三边的整厘米长度可能是：5、6、7、8、9、10、11、12、13cm。

　　如果考虑小数结果，则会发现，可能的三角形会有无穷多种。

,