三角形内角外角知识点（巧用三角形内角和180）

知识点：

三角形内角和180°

三角形的外角等于和它不相邻的两个外角之和

例题1、如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，则∠A=

思路点拨：

此类题条件中没有任何一个角的度数，只有边的关系，最后要求角的度数，思路由两种：

“特殊边的关系对应特殊角”或者是“利用内角和为180°建立方程”，而此题利用后者。

由BD=BC=AD得出：∠A=∠ABD，∠BDC=∠C，

由AB=AC得出：∠ABC=∠C，

为了方便计算，设∠A=x，则∠ABD=x，∠BDC=∠C=2x，∠ABC=2x，

在△ABC中，∠A ∠ABC ∠C=180°，x 2x 2x=180°，解得x=36°。

例题2、如下图所示，D为BC上一点，且AB=AC=BD，则图中∠1与∠2的关系是（ ）

A．∠1=2∠2 B．∠1 ∠2=180° C．∠1 3∠2=180° D．3∠1-∠2=180°

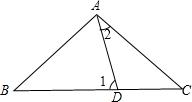
思路点拨：

看问题是找两角之间的关系，此类题的方法常常是利用内角和或者外角定理找关系；

由AB=AC=BD，得出：∠1=∠BAD，∠B=∠C，

题中问题是找∠1与∠2的关系，而利用外角定理可知：

∠1=∠2 ∠C，可转化为∠C=∠1-∠2，从而得出∠B=∠1-∠2，

在△ABD中，∠1 ∠B ∠BAD=180°，等量代换得∠1 ∠1-∠2 ∠1=180°,

化简得：3∠1-∠2=180°，即选D。

练习

1、如图1，在三角形ABC中，AB＝AC，D为BC边上的一点，且AB＝BD，AD＝CD，

则∠ABC= 36°

2、如图2，△ABC中，点D为BC上一点，且AB=AC=CD，则图中∠1和∠2的关系是（C）

A．∠2=2∠1 B．∠1 2∠2=90° C．2∠1 3∠2=180° D．3∠1 2∠2=180°

例题3、如图，已知AB=AC, ∠B=∠EDF，BE=DC，证明：DE=DF

思路点拨：

（1）根据结论，初步判断需要证明：△BDE≌△CFD或者是证明∠DEF=∠DFE。

（2）结合条件AB=AC（∠B=∠C），BE=DC判断，证明△BDE≌△CFD可能性比较大，因为已

经有2个条件了，接下来找第3个条件；发现∠B=∠EDF还没有用，怎么用？看（3）

（3）因为∠B ∠BDE ∠BED=180°，∠EDF ∠BDE ∠FDC=180°，推出：∠BED=∠FDC，

到此全等条件已经具备，利用ASA判定△BDE≌△CFD即可。

此题还可以用外角定理来完成∠BED=∠FDC的证明，在我的文章里已经专题讲解过，欢迎查

找之前的文章。

各位好友，后续会持续更新等腰三角形问题，相互学习，谢谢关注！