六种方法帮你解决模型过拟合问题（拉格朗日对偶模型臆想之KKT凸优化和强弱对偶）

上篇（第二十九篇）对拉格朗日对偶模型的剖析中，小白对关于拉格朗日乘子的理解还是满意的，即拉格朗日乘子的本质在于描述对偶问题所关联的对偶函数空间彼此膨胀（彼此约束）的数学建模。但是对"相加"（拉格朗日函数表示为问题函数和约束函数"相加"）的解释不甚满意。因此，本章内容首先会再次分析拉格朗日函数，得出"相加"的含义是问题函数和约束函数对偶关系的数学建模。接着，小白会引出凸优化，KKT条件以及强弱对偶，进而更完善的完成关于拉格朗日对偶模型的理解。

第三十篇 拉格朗日对偶模型臆想之KKT凸优化和强弱对偶拉格朗日函数"相加"的含义

图1

如图1，对于函数Z=f(x,y)。可以理解为，f是一个面（x,y）到一个标量数轴Z的映射，每一个Z的取值h对应着平面（x,y）上一条线h=f(x,y)，这条线可理解为一维的空间。即，Z=f(x,y)把面（x,y）分割成了无数个h=f(x,y)空间，Z的变化对应着不同空间。

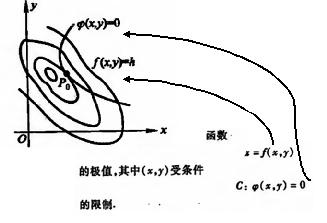
图2

因此，如图2，我们可以把问题函数f(x,y)和约束函数Q(x,y)看成是对平面(x,y)以不同映射方式分割而成的无数个函数空间。其中一个问题函数空间对应着问题的极值，其中一个约束函数空间对应着约束的边界（Q(x,y)=0）。

小白感觉，从函数空间角度去理解似乎很好，很清晰。此刻，回到问题本身，我们的目标是对于"约束条件下的问题函数的极值"建模，即，在特定的约束函数空间边界，问题函数空间的边界在哪呢？

我们发现，问题函数空间和约束函数空间都在（x,y）的平面上，因此，我们只需要朝着约束函数边界的方向去寻找，找到和约束函数边界相切的问题函数空间，切点（P0）的坐标就是我们问题的解，问题空间对应的Z的值就是我们要找的极值。

因此，我们理解，Q(x,y)和f(x,y)相加，背后的含义是问题的极值和约束边界交合，一方的增加，另一方是必减少，此消彼长，对偶而生。相加是对 对偶关系的建模。

我们在此顺便理解下拉格朗日乘子，其背后的含义是和约束函数空间边界相切的问题函数空间伸缩度的度量，这个度量就是切点的斜率。

趁热打铁，我们再来理解下拉格朗日对偶函数L（x,y,a）。

拉格朗日函数L的含义

如上是拉格朗日函数，先从约束函数开始，对于约束空间，体现为在平面（x,y）上的一条曲线，如下图3中的黑色曲线。

图3

然后，我们再想，这条曲线由经过f(x,y)的映射，变成了如图3中的红色的曲线。这个曲线就是L，这个曲线L在(x,y)上的投影是约束函数的函数空间，同时，这个曲线又由问题函数空间f（x,y）膨胀而成，因此，曲线L(即对偶模型函数)是问题函数和和约束函数的 双重叠加。另外，拉格朗日乘子就是红色曲线最高点的斜率。

引出KKT条件

图4

如上图4，约束条件可能是不等式。这时，约束空间由边界曲线变成了有边界的面。这种情况，我们不难分析 ，其等同于等式约束的情况。

图5

如上图5，假如不等式 约束函数是凸的，那么可能出现如上情况。这种情况，我们不难分析，这时候约束是无效的，即，无约束的情况。

对于上面图4和 图5两种情况 ，在拉格朗日对偶模型里，通过KKT条件进行概括；

KKT条件

通常，我们扩展一个广义的拉格朗日函数，同时包含等式约束和不等式约束的情况，如下：

对于的KKT条件是：

其中：

（1） 是拉格朗日函数解的条件；

（2） 被称作松弛互补条件，其目的是覆盖上面图4和图5的情况，即考虑到约束函数有效和无效的情况，比如beta为0，其实约束是无效的；

（3） 和（4）是原约束条件；

（5）拉格朗日乘数，即约定。度量边界的膨胀率。

引出凸优化

图6

如图6。我们可能会想到，约束函数空间边界如上图6中红色曲线时，情况将会如何？我们知道实际的极值点可能是P0点，但我们可能找到了P1。这时，我们有一种直观上的感受，就是约束边界如何表现为向外凸起的形状时，切点即为极值点的结论才是正确的，即在非凸的（Non-convex）情况下，我们找到的极值点，可能不是全局最优的。因此，拉格朗日对偶模型常会考虑问题函数和约束函数是凸集的一些场景，我们称之为凸优化问题 。下面列出一些常用的凸优化拉格朗日对偶模型。

注：如果对偶模型遇到非凸函数时该如何处理呢，小白思考，我们应该可以尝试把非凸问题转化为凸问题，这样就可以了。当然，下面还会谈到弱对偶，是与非凸情况相关的。

"凸"的定义

首先，如下是凸集的定义：

如上定义2.1对于凸集的定义，很容易形象化的理解，即一个凸集的元素x和元素y之间连线上的任一元素都属于当前的凸集。定义3.1是关于凸函数的定义。

线性凸优化模型

如上，线性凸优化模型。我们可以理解，线性凸优化模型的问题函数和约束函数都是凸的，其实它满足2.1凸定义中的等式条件。

二次规划模型

如上，二次规划模型定义，即QP。我们看到，问题函数对于资源空间x是二次的，是凸函数（想象抛物线是凸的）；约束函数是线性函数，也是凸的。

二次约束二次规划模型

如上，二次约束二次规划模型，即QCQP。我们看到，问题函数和约束函数都是二次的，都是凸的。

半正定模型

如上是半正定模型，回顾小白《对矩阵的线性臆想》一文，tr表示矩阵的"迹"。半正定规划也是凸的。

强对偶与弱对偶

从字面上看，对偶必有两者，意为问题函数和约束函数。一是从问题本身出发解决问题，二是，从约束出发解决问题。下面我们从约束函数的角度出发，来解决问题。从而得出与问题函数的强弱关联。

如果我们直接求解问题函数，我们是求解L(x)的最大下确界（inf）

我们如果x看作常量 ，把拉格朗日乘子看作变量，如下：

下面我们仅考虑问题函数f(x,y)和仅有一个约束函数h(x,y)的情况。这样我们只考虑h(x,y)映射的Y和f(x,y)映射的Z的情况，如下图，Y和Z形成了一个封闭的空间G：

图7

如图7，从（Z,y）的空间看，极值点就是Ｐ0处。而拉格朗日乘子就是P0处的切线的斜率。我们知道，对如上图的凸区间G，拉格朗日乘子变化（即对偶问题自变量的变化），可形象的看作上图中切线沿着闭区间的边界运动，因此，一定是能和P0点重合的。因此，这就体现了从对偶的角度解决问题。

图8

我们再考虑如上图8的情况，（Z,y）的空间G非凸区间内。我们发现沿着G的边界是永远找不到最优的点（上方红色的点），但是我们可以找到一个次优的点（下方红色的点）。而我们称此时，问题和对偶问题时弱对偶的，对偶问题的解和实际的解有差距，我们称这个差距（红色点之间的距离）称为对偶间隔。

如下图，我们再从解决问题函数角度看，可能是如下这种情况，即约束函数的非凸特点，造成了弱对偶。

图9

因此，我们理解 ，非凸的问题函数或约束函数，可能是弱对偶的；凸优化是强对偶的。

,