常见决策模型（模型思考者3三种分布模型）

这里是斯科特·佩奇的《模型思考者》这本书的第三讲，咱们讲三个特别常用的统计模型，分别是“正态分布”、“对数正态分布”和“幂律分布”。

我敢打赌你至少听说过“正态分布”。我们专栏以前提到过正态分布 [1]，这次是以模型的眼光把三个重要分布放在一起讲。佩奇的模型课完全不介意使用数学，这三个概念听起来就有强烈的数学味道……而我保证，在我们整个的系列解读中，你都不需要拿起笔来做数学计算。

但是你需要从这个系列中获得一点“数学感”。球迷自己不会踢，看别人踢球也会得到有一点“球感”，也能在一定程度上阅读比赛、甚至做出很好的预测判断，我说的数学感差不多也是这个意思。

这一讲说的数学感能带给你一个非常实用的判断力：什么时候应该担心发生极端事件，什么时候不应该担心。我们讲“蝴蝶效应”的时候说过 [2]，就算你是个小心谨慎的人，你也不应该一天到晚对什么事情都提心吊胆。

有些天真的人认为极端事件随时都可能在任何领域发生，真正的学者不会这么看问题的 —— 我们的确见过很多身高超过两米的人，但是可没见过身高 15 米的人。而在另一些领域中，的确就是存在特别极端的例子，比如世界上有些特别有钱的人。这二者的区别是啥呢？

区别是人的身高服从正态分布，而财富不是。

1.正态分布

咱们先回到上一讲说的那个开餐馆的事儿。如果你的餐馆事业已经比较稳定了，你不会太担心顾客流量的波动。这种情况，就是正态分布。

假设你的餐馆平均每天有 100 个顾客，比较好的时候能到 115 人，比较差的时候也有 85 人，那么画出图来，就是下面这样的一条钟形曲线 ——

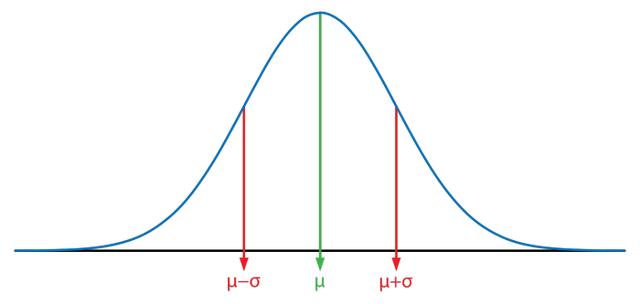
曲线的横坐标代表每天来的人数，纵坐标代表在比如说一个季度之中，来这么多人的时候有多少天。图中标记了正态分布的两个重要概念：平均值（μ），和标准差（σ）。对你这个餐馆来说，μ = 100，σ = 15，这意味着在 68%的日子里，你的顾客人数会在 85 和 115 之间 —— 这叫“一个标准差之内”。横轴上距离平均值越远的地方越是极端事件，而那些事件的纵坐标大小则代表它们发生的概率。

只要你知道餐馆人数符合正态分布，平均值和标准差就都可以用平时的流量数据统计出来。有了平均值和标准差你就可以大致估算各种事件发生的概率：95%的事情都发生在两个标准差之内，99.7% 的事情发生在三个标准差之内。有个极客说要找个美貌程度在两个标准差之外的女朋友，那就意味着她要比 97.5%的人都漂亮。

这些概念是一名现代大学生应该具备的常识，你在课堂上可能都学过。但是也许你有个疑问：

为什么餐馆人数满足正态分布？

并不是所有随机事件都满足正态分布。想要学会判断什么样的事件满足正态分布，你必须有一点数学感，你需要了解“中心极限定理”。中心极限定理说，如果一个事件满足下面这些条件，它的分布就是正态分布 ——

第一，它是由多个 —— 至少 20 个 —— 随机变量*相加*的结果；

第二，这众多的随机变量是互相“独立”的；

第三，每个随机变量的方差都只有有限大；

第四，每个随机变量对结果都要有一定的贡献，否则如果只是其中几个起到决定性的作用，那也不能算“多”。

简单地说，关键要求有两个：“相加”和“独立” —— 凡是多个独立随机变量相加的事件，结果就会是正态分布 [3]。

你的餐馆顾客满足这些条件。每个顾客来不来吃饭都是他自己的决定，是独立的；而你计算的是今天总共来了多少人，是这些人的和。

直观地说，中心极限定理说的是每个人来不来可能波动很大，但是因为人多，整体上来多少人，波动就不会有那么大，所以满足正态分布。

生物学家认为人的身高是由至少 180 个基因共同决定的。有的决定你的小腿有多长，有的决定你的脖子有多长 —— 而你的身高，是所有这些因素相加之和。作为一个很好的近似，决定身高的各个基因是比较互相独立的。所以身高满足正态分布。

你看这是不是有一种“冥冥之中自有定数”的感觉。虽然你不知道明天会有哪些顾客，但是你知道他们的总人数不会太离谱：三个标准差已经覆盖了 99.7%的可能性，来超过 145 或者低于 55 人的可能性只有千分之一。这意味着两三年都碰不到一次，所以你真的没有必要准备那么多桌椅。

正态分布能给人充分的掌控感。每个案例相差都不会很大，通常翻不了天。

好，现在回到正态分布的两个条件，“相加”和“独立”：如果局面不满足这两个条件，结果会是怎样的呢？那你就得做好准备迎接极端事件了。

2.对数正态分布

如果一个事件的结果不是由独立随机事件相加、而是由相乘决定的，它的分布将是“对数正态分布”。这个分布的形状就不是对称的钟形了，而是像下面这样 ——

它有一个比较长的尾巴。这意味着其中发生极端事件的可能性比正态分布高很多。

比如说涨工资吧。有个公司，本来员工之间工资相差不大。有一天老板宣布了一个涨工资计划，说以后每年业绩突出的员工，工资会增加 10%。你猜这个政策意味着什么？

意味着员工之间的工资差距将会变得越来越大。可能老王工资本来就比小李高，这次业绩又比小李好，那么老王涨 10%，小李没有，所以两人的差距将会变大。换一种情况，老王表现没有小李好，那么小李涨 10%，两人差距会缩小。但是，请注意，因为老王工资高，所以第一种情况导致的工资差距拉大，会超过第二种情况导致的工资差距缩小 —— 所以总体看来，全体员工的收入差距必然拉大。

这就是因为你使用了相乘的方法。换个方案，如果规定业绩好的员工，不论之前的工资是多少，一律涨一万块钱，那么员工之间的工资差距就不会拉大。

你喜欢让员工的收入差距拉大还是缩小呢？不管你喜欢哪种局面，你需要这个数学感。否则是你自己设计的模型，含着泪也得接受它的结果。

请注意，对数正态分布仍然假设每个随机变量的作用是互相独立的 —— 这意味着哪个员工今年能做出更好的业绩，跟他去年的工资没关系。而如果你认为员工工资代表了能力，那么工资越高的人就越有可能做出好业绩，那结果就不会是对数正态分布了，而是比这还要容易出极端事件的“幂律分布”。

3.幂律分布

幂律分布的“长尾”，比对数正态分布更长 ——

网页链接的幂律分布

对数坐标下，幂律分布（黑线）和对数正态分布（灰线）的比较

这意味着幂律分布中会有大量的极端事件。

幂律分布是*不独立*的随机变量作用的结果。科学家找到了很多个能带来幂律分布的模型，咱们这里说其中最常见的两个。

第一个模型是“马太效应”。比如你去书店买书，那么多本书选哪本呢？你会优先关注那些上了排行榜的“畅销书”。这是人之常情，但是这对那些没上榜的书是不公平的 —— 这等于说越畅销的书就会越容易被关注，而越容易被关注就让它进一步更畅销。这就成了一个富者愈富的局面。幂律分布使得图书市场中会出现少量特别畅销的书，而绝大多数书的销售成绩都很差。

而这一切都是因为你做决定的时候是在模仿别人。你看到别人都买这本书，所以你才关注它。你的买书行为不是独立的。

明星的粉丝数量、公司的大小、城市的大小，都是幂律分布。比如一个城市越大，其中人与人的互动就越多，就业机会和创新机会也会越多，就越能吸引到新人的加入。这就是为什么中国有那么多的超大城市。当然每个幂律分布中的那个幂律参数不见得是一样的，但是这一讲我们不关心具体的数学，只关心数学感。

如果一个局面中有很多极端事件，我们基本上可以猜测它满足某种某种幂律分布。佩奇做了个计算，说如果美国人的身高是幂律分布的，全美国就会至少有一个人比帝国大厦还要高，而且有一万人会比长颈鹿高……这就是幂律分布的威力。

另一种幂律分布模型来自于复杂系统的“自组织”现象。一个系统在变大、变复杂的过程中，它的各个部分互相依赖的程度将会增加。到了一个临界点，因为互相关联实在太紧密了，一部分出个小问题就会导致整个系统出大问题，那就是雪崩式的灾难。

核电站的安全性、地震、森林大火，这些事情中包含自组织，各个部分之间会有复杂的联动。而我们说过，所谓蝴蝶效应，罪过不在蝴蝶，恰恰就是因为系统中的复杂联动。这些系统可能平时什么事儿都没有，但是其中蕴含着大灾难的可能性。

可能一个地区每天都发生一万次以上的小地震，影响微不足道，但是你考虑到地震是幂律分布的事件，就必须对大地震做好防灾准备。

*

总而言之，如果这个事件代表多个独立随机变量之和，它就满足正态分布，你不用担心会有什么极端的情况发生。如果一个事件是独立随机变量的乘积，那就是对数正态分布，其中会有一些比较极端、但不是那么极端的事情发生。而如果一个事件中的随机变量不是互相独立的，有互相模仿或者达成了紧密的关联，那你就必须做好应对极端情况的准备。

如果你是一个管理者，这个数学感会让你希望建立一个“原子化”的组织。其中的个体都独立决定，不要互相模仿、不要有什么民间组织和派系，实现正态分布。这意味着你要打压那些所谓一呼百应的“社会凝结核”，你要把坏消息的传播控制在最低限度。

而作为个体，也许幂律分布对你有某种诱惑……咱们会专门说说这个。

,