数学概念与方程（数学笔记基本方程）

方程是含有未知数的等式。

解方程的一般步骤：去分母——去括号——移项——合并同类项——系数化为1

分析实际问题中的数量关系，利用其中的相等关系列出方程：设未知数，列方程，解方程，检验结果，确定答案。

一元一次方程

通常形式: ax b = 0 (a，b为常数，且a≠0）。

例：整理一批图书，由一个人完成要40 h。现计划由一部分人先做 4 h，然后增加2人与他们一起做 8 h 完成这项工作。假设这些人的工作效率相同，具体应先安排多少人工作？

分析：如果把总工作量设为1，则人均效率(一个人1h完成的工作量)为1/ 40 ，x人先做4h完成的工作量为4x/40，增加2人后再做8h完成的工作量为8(x 2)/40 这两个工作量之和应等于总工作量。

解：设安排x人先做4h，根据先后两个时段的工作量之和应等于总工作量，列出方程：

4x/40 8(x 2)/40 = 1

解方程，得: x = 2

答：应先安排2个人工作。

二元一次方程组

二元一次方程组中有两个未知数，如果消去其中一个未知数，就把二元一次方程组转化为一元一次方程，先求出一个未知数，再求出另一个未知数，这种将未知数的个数由多化少、逐一解决的思想，叫做消元思想。代入消元和加减消元是二元一次方程组的两种解法。

三元一次方程组

解三元一次方程组的步骤

一元二次方程

一般形式：ax² bx c=0(a≠0)

解一元二次方程:

1.配方法 ( x n )² = p

p＞0 ，有两实根，p=0，有两个相同的根；p＜0，无实根。

2.公式法

一般地，式子 b²- 4ac 叫做一元二次方程ax² bx c=0 根的判别式，通常用希腊字母“Δ”表示它，即 Δ=b²-4ac 。

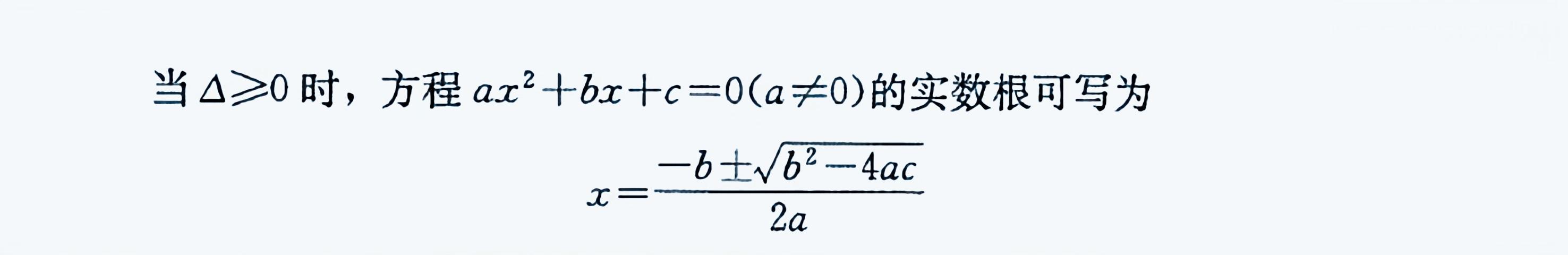
求根公式

3.因式分解法

使方程化为两个一次式的乘积等于0的形式，再使这两个一次式分别等于0，从而实现降次的方法叫做因式分解法。

因式分解例题练习

一元二次方程的根与系数的关系:

一元二次方程的根与系数的关系

分式方程

一般地，如果A，B表示两个整式，并且B中含有字母，那么式子A/B叫做分式，其中，B≠0。

分式的基本性质:

分式的基本性质

根据分式的基本性质，把一个分式的分子与分母的公因式约去，叫做分式的约分。分子与分母没有公因式的分式，叫做最简分式。根据分式的基本性质，把几个异分母的分式分别化成与原来的分式相等的同分母的分式，叫做分式的通分。通分要先确定分式的最简公分母。

分式的运算法则:

分式的加减法则

分式的乘除法则

分式的乘方

分母中含有未知数的方程叫做分式方程。

解分式方程的一般步骤

,