初中数学圆的图形（初中几何10三角形的旁切圆）

这里我们先再了解一下三角形的五心之一——旁心。

三角形旁切圆的圆心，简称为三角形旁心，它是三角形一个内角的平分线和其他两个内角的外角平分线的交点；显然，任何三角形都存在三个旁切圆、三个旁心。

旁心主要有4个性质：

性质1 ：三角形的一条内角平分线与其他两个角的外角平分线交于一点，该点即为三角形的旁心。

性质2：旁心到三角形三边的距离相等。

性质3：三角形有三个旁切圆，三个旁心。旁心一定在三角形外。

性质4：直角三角形斜边上的旁切圆的半径等于三角形周长的一半。

前3个都容易理解，这里主要讨论一下第4个性质：

证明如下：

圆F为直角△ABC斜边BC上的外切圆，切点分别为D，E，G，

因此FE=FG=FD，可得两组全等三角形：

△BEF ≌ △BGF

△FGC ≌ △FDC

∴ BE=BG，GC = CD

且四边形EFDA为正方形

∴ EF FD = BE BA DC CA

且 BG CG = BC

∴ BA AC CB = EF FD = 2r

即，斜边上的旁切圆的半径为直角三角形的半周长

证明完毕

前面的章节里介绍了直角三角形的内切圆半径是：

因此对于等腰直角三角形，内切圆圆心和斜边的旁切圆的圆心的线段长度为两条直角边的和。

即，DK = AB AC（圆D和圆K相切与F点）

在解题中，对三角形旁心的使用比较少，遇到时，如果看不出的话会比较棘手。

如下题：

四边形各角如下，求∠DBC角度？

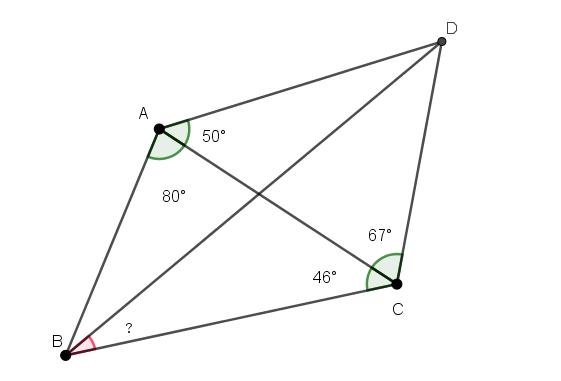
咋看之下没有头绪，当我们延长BA和BC之后会发现AD和CD是两个外角的角平分线，点D为AC边的旁切圆，那么BD就是∠ABC的角平分线。因此

∠DBC = (180 – 80 – 46)/2 = 27°