判别式法求函数值域（105判别式法求函数的值域）

前面讲了，当遇到分子分母都是一次函数形式的函数的时候，可以用分离常数法解决，但如果遇到分母是二次函数形式的函数，应该怎么做呢，我们一般采用的是：

判别式法

解题模板：

第一步 观察函数解析式的形式，形如

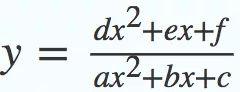
的函数；

第二步 将函数式化成关于x的方程，且方程有解，用根的判别式求出参数y的取值范围，即得函数的值域.

例：

函数的值域，本质上是y的取值范围，而y的范围是由x决定的，每个x必须有意义，如果把函数写成关于x的二次方程，方程必须有解，也就是二次方程的判别式要大于零，从而解出y的范围，就函数的值域。

大家可以试试看，然后再看下面的解析哦

看明白了吧，可以试试下面的练习

变式训练：

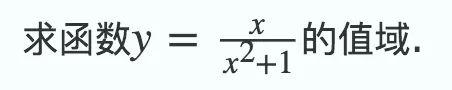
大家可以自己做做看。如果有任何问题，可以给我留言哈。

开心教练有话说：

许多同学会觉得教练发的题目太简单了，但所有难的题目都是有简单的题目演化而来的，得先把这些所谓“简单”的题目搞定，才谈得上做难题，从另外一个角度来看，高考的大部分题目都是简单到中等的题目，把这些题目搞定了，基本就在120分（满分150）以上了，所以希望大家认真巩固这些基本题型，熟练掌握这些题型，才能在考试的时候留出更多的时间思考难题，让你的成绩更上一层楼。