特殊三角形面积的计算（关于n维三角形面积）

数学上关于三角形面积的公式花样繁多，

基础的S=（1/2）ah，这是伴随我们整个小学的三角形面积公式，我记得那时候为了求一个三角形的面积，我还要拿着三角板、直尺在那里比来比去的，就连数学老师看着都着急。

直到初中，就会了点其他的东西，比方说等腰三角形的面积，告诉了三边长，先勾股定理，在底乘以高的一半就行了，当时学了勾股定理的时候，整个人都高兴的不得了，就感觉自己比毕达哥拉斯还伟大。

然后吧，就在高中学习了一些乱七八糟的东西，就比如S=（1/2）absinC，还比如正三角形的面积公式

正三角形面积，边长为a

我们的数学老师就说过，高中三年这个公式都记不得，那这个高中就没有营养了。任何数学老师都不会不讲海伦秦九韶公式的，我的数学老师也不例外，最主要的是他还用余弦定理给我们推了一遍，当时我就十分崇拜他，当然他也曾经说过，他在我们省发表过关于高中三角形面积的公式全集，获得了省奖[灵光一闪]

！！（说歪了）

当然之后，学了直线之后，三角形面积就变得解析化了，已知三角形三个点的二维坐标，建立方程，点到直线的距离，两点间距离公式，三步搞定。

当然既然我都说了是维度问题，能升华到维度上的，向量绝对是先锋！！那么这篇故事的重点来了！

之前谈到了S=（1/2）absinC，这很诱人，不禁让人想起向量点积公式，可是要乘cos！！！我们可以知道sin²C＋cos²C=1，而且在三角形内，sinc＞0

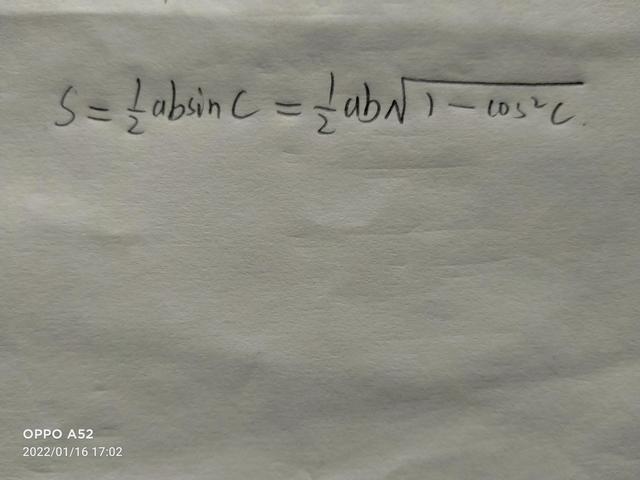
这就让人想这样

还想这样

又想这样

所以就这样了

接下来

当然，由于我自学了一点儿矩阵，我把他化成了

正规一点儿，是这样的

后来我自己运算了三维的，得到了这个玩意儿

你没看错，就是这玩意儿

后来，我猜想了一下

图1..

是的你没看错，就是这个玩意儿，我现在其实不知道是不是对的，但是

图2..我不知道和上一幅图是不是等价的

直觉告诉我，第一个应该正确，若果第二幅图等价，那也应该正确。但是我觉得第二幅应该凉凉，所以我其实希望有大佬能帮我证明！错的也无所谓。