九上数学相似三角形判定的证明（相似三角形判定定理证明浅见）

初中阶级，相似三角形的判定，只给出了判定的方法，并没有给出这些方法的证明，在这里，我想对这些方法的证明，给出我的浅见。

相似三角形判定的方法主要有三个：

方法一：如果一个三角形的两个角分别与另一个三角形的两个角对应相等，那么这两个三角形相似。

方法二：如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。

方法三：如果一个三角形的三条边和另一个三角形的三条边对应成比例，那么这两个三角形相似。

---

方法一

ΔABC和ΔADE中，∠BAC=∠DAE,∠ABC=∠ADE,求证：ΔABC∽ΔADE。

为了方便证明，将两个三角形合并到一个图形当中。

首先证明三个角对应相等。

∠BAC=∠DAE,∠ABC=∠ADE,可以推出∠ACB=∠AED。

三个角对应相等证明完，接下证明三角边对应成比例。

∠ABC=∠ADE，可证出BC//DE，可得AB:DB=AC:CE=k。

设AB=a,BC=b,得AC=ak,CE=bk。

作CF//AD，可得CE:AC=EF:DF=k1,

可得，EF=bk1,DF=ak1.

四边形BCFD是平行四边形，可得BC=DF=ak1。

可得AB:AD=AC:AE=BC:DE=a:(a b)

所以，两个三角形相似。

方法二

这道题主要运用到平行线分线段成比例逆用，也就是，直线分线段成比例，那么直线平行。

如图所示，AB:BD=AC:CE，求证：BC//DE.

这个用到反证法。

若BC不平行于DE，那么过D点作DF//BC,与AE所在的直线相交于F

可得,AB:BD=AC:CF.

因为AB:BD=AC:CE，所以CE=CF，可知E、F两点重合。

所以BC//DE。

接下来我们来证明方法二

为了方便，还是将两个三角形合并到一个图形中。

ΔABC和ΔADE中，AB:AD=AC:AE，求证：ΔABC∽ΔADE。

AB:AD=AC:AE，可得BC//DE，可得∠ABC=∠D。

所以，两个三角形相似。

方法三

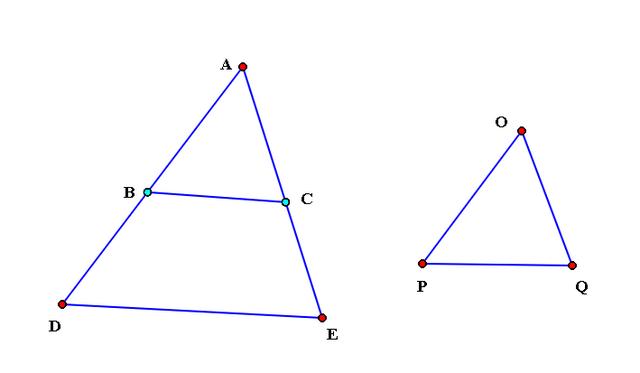
ΔADE和ΔOPQ中,AD:OP=AE:OQ=DE:PQ.

作AB=OP，AC=OQ，

可得，AB:AD=AC:AE，

可得，ΔADE∽ΔABC，

可得，BC:DE=AB:AD=AC:AE。

可得，BC=PQ。

可得，ΔABC全等于ΔOPQ

所以，两个三角形相似。

,