为什么星球都是悬浮的（为什么星球都是球形的）

这里我将尝试用最简单的方式来回答这个问题。

回答这个问题的关键词是流体静力学平衡（hydrostatic equilibrium）。看起来是一个令人望而生畏的专业词汇，不过理解它其实只需要中学物理知识。

下面这一杯水处于平衡状态，也就是说，每一滴水都是静止的（这里不考虑分子热运动）。牛顿第一定律告诉我们，里面的每一滴水受到的合力都是0。

考虑其中一个很小的水块，它受到的力包括上下左右四个方向的压力。由于它受到的合力为0，所以，在垂直方向和水平方向的两个力都是相等的。同时，流体的特性告诉我们，其实这4个力都是相等的：它们等于这个水块上面的水的重力。

为了让讨论变得简单，这里对实际情况作了很多简化。比如，因为这个水块很小（可以认为它无穷下），我们忽略了它自身的重力；水中的压力来自三维空间的所有方向，这里我们把它简化为二维空间中的上下左右。

如果水面不平，它对下面的水块会有什么影响呢？

考虑图中的同一水平高度上的三个水块。水块A和C都对水块B产生水平方向的压力，而这个压力等于它们（A和C）上面的水的重量。在水面平整的前提下，A和C对B的水平方向压力是相等的，所以B在水平方向上保持静止。

现在水块C上面不知道为什么多了一团水。当然，在真实情况下，这团多余的水很快就会向两边流动，让水面恢复平整。但是这里我们先不考虑它自身的变化，来看看它对下面的水块有什么影响。

水块C受到的压力显然大于水块A受到的压力了，那么C对B的水平压力也相应地大于A对B的水平压力。这时，水块B就无法保持静止了，它会向左边移动。

这里我们只分析了水块B的受力和运动情况。实际上，这杯水是由无数水块组成的。在水面上产生额外的压力的情况下，这样的受力变化和运动发生在每一个水块上面。所以，大量的水块都会在这个压力作用下向四周运动。你很容易想象这种运动的结果是什么：让那个多余的水块下落，最后让水面恢复平整。

讲了半天好像还没有提到星球。下面我们就来看看一个星球的例子。假设有这么一个完全由水构成的行星，我们也可以认为它包含着无数无穷下的水块。

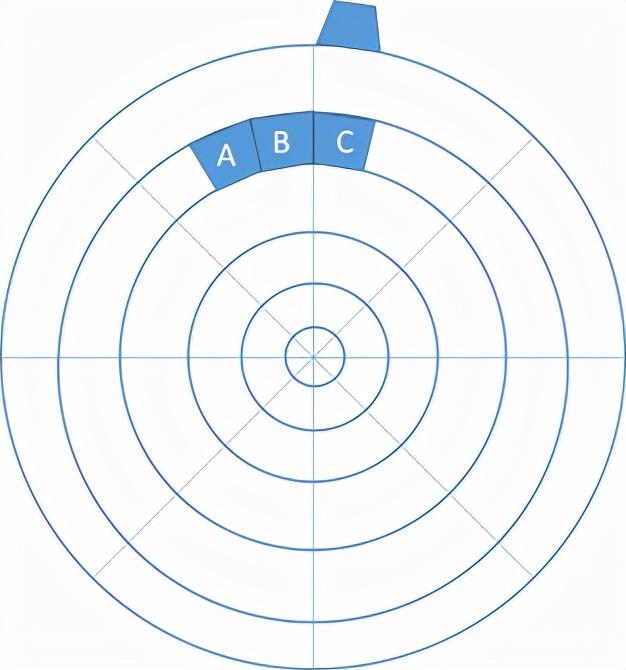
现在这个星球并不是球形的，比如，水块C上面多了一团水。用上面相同的方法分析我们会得到相同的结果：这团多余的水会破坏下面水块的平衡状态，从而把它们挤开，腾出空间让这团水落下来。

你可以尝试不同形状的水星球，比如立方体，正四面体，椭球体等等，然后用上面的方法分析。你会发现这些形状都无法让星球中的所有水块达到受力平衡状态。结果是，水块在受力不平衡的情况下会运动，最后找到一个唯一可以让大家都相安无事的形状——球形。

上面回答了一个液体星球为什么必须是球形的。像地球这样的岩质行星是由强度极高的固体构成的，为什么也是球形的呢？原因很简单，在极高的压力下，像岩石一样的固体也会表现出液体的特性。比如，山脉会折叠而不会折断，地幔甚至会用对流的方式传递热量。

让固体产生流体的特性需要极高的压力，在星球内部，这个压力来源于自身的引力，而引力来源于质量，所以，只有质量达到一定限度的星球，才会变成球形。同时，一个星球能否达到流体静力学平衡状态，也和构成这个星球本身的材料有关。

星球内部的物质受到的压力来自于它上面的物质的重量，所以，这个压力是随着深度逐渐增加的。这就意味着星球表面的物质受到的压力很小。这个事实就允许岩质行星的表面不必像水面那样平整。它可以有高地，平原，山脉和深谷。

即使不考虑表面的各种地形，星球也很少有完美的球形。由于自转的原因，其实它们大多数是椭球体。我们回到前面的水行星上来讨论这个问题。在一颗自转的水行星上，所有的水块都在以相同的角速度运动，但是它们的旋转半径不一样。

根据向心力公式： F = m r w^2 可知，圆周运动的向心力是和半径成正比的，所以，距离自转轴越远的地方（如地球的赤道），向心力就越大。如果我们比较赤道附近和两极附近的水块，可以看出，如果它们上面有一样多的水，它们受到的压力是不一样的。因为，赤道上的一部分压力被用来做维持圆周运动的向心力了。要让所有的水块达到受力平衡状态，赤道上的水块上面需要有更多的水。也就是说：只有椭球形才能让所有的水块达到受力平衡状态。

如果自转速度太快的话，一颗行星可能会变成你意想不到的形状。