八省联考数学填空题解析（八省联考解读数学）

随着新高考步伐的推进，今年参加新高考的省份又新增了广东、福建、辽宁、江苏、重庆、湖南、湖北、河北这八个省份，为了让这些省份的学生能提前适应新高考，教育部组织了有史以来最大规模的一次八省联考，根据这次八省联考试卷，我们现在一起就从以下五个方面去深度对比和了解此次八省联考试卷与老高考和山东海南新高考试卷的变化与相似之处。

1从试卷整体结构上分析

（一）题型、题量及分值变化

如上表，八省联考和新高考题型和分值大体上比较相似，新高考与老高考相比，变化还是比较的大，具体为：

1.八省联考与新高考相比，出现了一道多空题。

2.新高考的选择题由8道单项选择题和4道多项选择题组成，其中多项选择题部分选对得3分，老高考选择题由12道单项选择题组成。

3.新高考解答题有6道题，而且全部都是必答题，而老高考解答题有5道必答题和一道选做题，选做题是2选1的模式。

（二）八省联考考点分布：

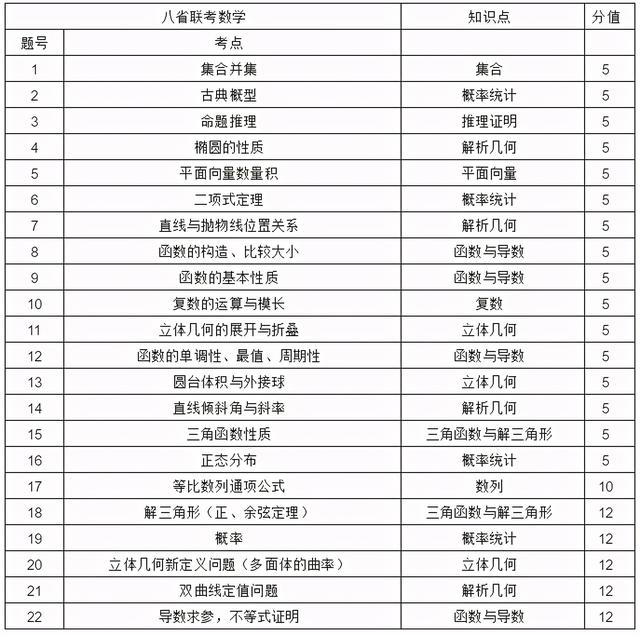
八省联考数学知识点分布

本次考试考查了八大主干知识：函数、导数、三角函数、平面向量、数列、立体几何、解析几何、概率统计。但是重点考查的知识点依旧是函数与导数，三角函数与解三角形，立体几何，解析几何，概率统计等，其中函数与导数，圆锥曲线以及概率统计分值占比最高，达到54%，也就是说这三个知识点占了将近一半的分值，平面向量和数列在本次考试中的占比不高，其中平面向量只有一道选择题。

从试卷的整体分布来看，本次考试的题目新颖度方面有了很大的提升，重点考查学生对于知识点的迁移能力。本次考试，题目比较新颖，思路技巧含量很高，而且本次考试最大的一个特点就是活。从第1题开始，几乎没有套路题，第一题需要结合韦恩图来做才比较快，不像以前的题目，简单口算就可以出来。第15题，是一道开放题，非常简单，理论上讲，你可以写出无数种正确答案。有些题新的让人不敢置信，第20题，考查立体几何的新定义题目，完全颠覆了固有的形态，直接给学生关于曲率的定义，然后根据定义做题。

本次考试还考查了学生的抗压能力，难度分布不再是由简单到难的分布，而是很多题目都可以出难题，以前觉得简单的知识点也有可能会出难题。比如第10题考查复数的运算与性质，以前复数都是送分题，但是这道题目运算量比较大，难度不是很大。第17题，第一道大题考查数列的相关知识，第一问很简单，但是第二问很难想到，需要技巧和方法才能做出来，这道题目拿满分不太容易，估计大部分都空着第二问，第一道大题一空，必然影响后面大题的做题心情。

本次考试的计算量还是比较大的，第7题，考查直线与抛物线位置关系，题目本身不难，大部分同学都能想到，但是运算量相当大，第12题，难度比较大，运算量也是比较大的。

总之，这套试卷的含金量还是还高的，题目设计质量也很高，而且需要学生能够活学活用。在平时的学习中，不要过分地依赖套路，不要过于依赖机械刷题，要有意识的提高学习和练习的难度，有意识的一题多解。要有意识地提高分析题目的能力，尽早形成分析、总结、归纳的习惯，有意识地培养学生的阅读文章、提取信息的能力。

2与老高考的不同类型对比

从表格对比可以看出老高考和八省联考在试题结构发生了比较大的变化，老高考的试题结构是12道单选题 4道填空题 6道解答题（其中5道必做题 1道选做题2选1），八省联考采用的试题结构是8道单选题 4道多选题 4道填空题 6道解答题，选择题数量不变，八省联考少了4道单选题，多了4道多选题，填空题数量保持不变，但八省联考此次出现了多空题及开放性填空题，答案不唯一，解答题结构变化也较大，老高考有5道必做题和一道选做题，试卷总的题数为23道，八省联考删除了选做题部分，试卷总的题数为22道，需做的试题总量与老高考保持不变。

从表格中可以观察出八省联考与老高考在知识点的分布及题型上有一些差异，尤其是立体几何章节版块，老高考采用的是1道数学文化空间几何体（单选） 线面垂直及求二面角（解答），此次八省联考考查的是1道立体几何的展开与折叠（多选） 1道圆台体积与外接球问题（填空） 立体几何新定义（解答），在解答题中立体几何变化较大，题目比较新颖，需要学生认真审题及理解题意，在复数考查方面变化也较大，复数出现在多选题是很多学生始料未及的，在八省联考中可以看出，在平时的学习中更需要学生加强对新事物的理解能力，这也能够体现出新高考的特点。

八省联考中试题结构存在的一些差异，具体表现在以下几题：

14.若正方形一条对角线所在直线的斜率为2，则该正方形的两条邻边所在直线的斜率分别为______，_____．

答案:

15.写出一个最小正周期为2的奇函数

________．

答案：由最小正周期为2，可考虑三角函数中的正弦型函数

，

，

满足

，即是奇函数；

根据最小正周期

，可得

.

故函数可以是

中任一个，可取

.

20．北京大兴国际机场的显著特点之一是各种弯曲空间的运用．刻画空间的弯曲性是几何研究的重要内容．用曲率刻画空间弯曲性，规定：多面体顶点的曲率等于

与多面体在该点的面角之和的差（多面体的面的内角叫做多面体的面角，角度用弧度制），多面体面上非顶点的曲率均为零，多面体的总曲率等于该多面体各顶点的曲率之和．例如：正四面体在每个顶点有3个面角，每个面角是

，所以正四面体在各顶点的曲率为

，故其总曲率为

．

（1）求四棱锥的总曲率；

（2）若多面体满足：顶点数-棱数 面数

，证明：这类多面体的总曲率是常数．

答案：（1）

；（2）证明见解析.

（1）由题可知：四棱锥的总曲率等于四棱锥各顶点的曲率之和.

可以从整个多面体的角度考虑，所有顶点相关的面角就是多面体的所有多边形表面的内角的集合.由图可知：四棱锥共有5个顶点，5个面，其中4个为三角形，1个为四边形.

所以四棱锥的表面内角和由4个为三角形，1个为四边形组成，

则其总曲率为：

.

（2）设顶点数、棱数、面数分别为

、

、

，所以有

设第

个面的棱数为

，所以

所以总曲率为：

3与2020年山东高考卷的对比

从上面表格可以看出此次八省联考与山东和海南新高考在试题结构上是一致的，都是采用8道单选题 4道多选题 4道填空题 6道解答题，但是也存在一些差异，在山东和海南的高考试卷中，是没有出现多空题和开放性试题，此次八省联考出现了多空题和开放性试题。

此次八省联考与山东高考卷相比在知识点的考查也存在一些差异，八省联考没有考查基本不等式及数学文化题，但是增加了创新试题（立体几何新定义），在立体几何中呈现的是分值增加，另外相比山东卷及海南卷，多选题评分有所变化，部分选对的情况由3分降至2分，故相对加大了学生对多选题准确性的把握，体现了新高考的特点，以提高学生能力为重的原则。

4创新类型

本次考试的题目中的创新点还是很多，通过这些创新点可以更好地指导后续的教学。

创新点：本题相比之前考查的复数的运算，难度有所增加，需要学生根据设出来的复数表达式去运算，运算量有点大。

从这道题目可以看出，简单的知识点也有可能出有点难度的题目，在以后的教学中，知识点都要求学生进行掌握，而不能仅仅停留在表面。

创新点：这道题目重新考查了圆台的体积，这个知识点很少考查，所以很多学生估计没有记住圆台体积公式。

从这个题目可以看出，现在考试不仅仅局限于以前的高频考点，像一些低频考点也是会重新考查的，所以在教学中，我们需要让学生掌握更多的知识点，而不再是只掌握一些高频考点即可。

创新点：这是一个开放题，理论上有无数个答案，只要求学生填写一个即可。

从这道题可以看出，现在题目越来越活，这道题只要静下心来，写个正弦函数即可，说明在日常的教学中，要充分让学生的发散思维。

创新点：考查立体几何的新定义题目，完全颠覆了固有的形态，直接给学生关于曲率的定义，然后根据定义做题。

从这道题可以看出，题目比较新颖，思路技巧含量很高，而且本题最大的一个特点就是活，所以需要平常的教学中，要多教学生活学活用，不能过多依赖套路。

5数学学科素养

第一题：

必备知识：本题主要考查的知识是“集合之间的关系”，“集合的并集的概念”和“集合补集的概念”，要求考生能够理解集合之间的关系、集合的并集的概念和集合补集的概念。

学科素养：本题考查的学科素养是数学探索。要求考生在理解集合之间的关系、集合的并集的概念和集合补集的概念的情景中得出正确答案。

第二题：

必备知识：本题考查的知识是“古典概型”和“组合问题”，根据古典概型的概念，通过组合得出概率。

科学素养：本题考查的学科素养是数学运算，要求学生理解古典概型，根据排列组合进行计算，得出正确答案。

第三题：

本题考查命题真假的判断，需要掌握二次函数根与系数的关系，根据二次函数根与系数的关系对甲、乙、丙、丁分别是假命题进行分类讨论，得出答案。

学科素养：本题考查的学科素养逻辑推理和数据分析，解题的关键就是对甲、乙、丙、丁分别是假命题进行分类讨论，结合已知条件求出方程的两根，再结合各命题的真假进行判断

第四题：

必备知识：本题主要考查的知识是“椭圆的标准方程”和“椭圆的定义”，要求考生能够掌握椭圆的标准方程和椭圆的定义。

学科素养：本题考查的学科素养是逻辑推理，数学运算和数据分析，分析出

为等边三角形，可得出

，进而可得出关于

的等式，即可解得

的值.

第五题：

必备知识：本题主要考查的知识是“向量的数量积”和“同角的三角函数关系”掌握向量数量积的概念。

学科素养：本题考查的学科素养是数学运算和逻辑推理，根据向量数量积的概念得出向量的夹角，再根据三角函数同角基本关系得出答案。

第六题：

必备知识：本题主要考查的知识是“组合公式：

”，了解组合公式。

学科素养：本题考查的学科素养是数学运算，根据组合公式：

求解。

第七题：

必备知识：本题主要考查的知识是“直线与圆的位置关系”、“直线与抛物线的位置关系”和“直线方程”。

学科素养：本题考查的学科素养是数学运算和直观想象，根据直线与圆相切，利用圆心到直线的距离等于半径得出切线方程，再求得正确答案。

第八题：

必备知识：本题主要考查的知识是“导函数求函数单调性”和“比较大小”。

学科素养：本题考查的学科素养是数学抽象，逻辑推理，数学运算，根据代数式的特征合理构建函数，再利用导数讨论其单调性，根据函数单调性比较大小。

第九题：

必备知识：本题主要考查的知识是“导函数求函数单调性”，“导函数的几何意义”，“判断函数的奇偶性”。

学科素养：本题考查的学科素养是数学抽象，逻辑推理，数学运算，根据代数式的特征合理构建函数，再利用导数讨论其单调性，根据函数单调性比较大小。

第十题：

必备知识：本题主要考查的知识是“复数”要求考生掌握复数代数形式的四则运算，了解共轭复数的概念。

学科素养：本题考查的学科素养是数学抽象和数学运算，根据复数代数形式的四则运算求解。

第十一题：

必备知识：本题主要考查的知识是“平面展开图”、“判断空间直线平行”和“判断空间直线垂直”，掌握空间量直线平行的判定定理和直线与平面垂直的判断定理。

学科素养：本题考查的学科素养是直观想象，逻辑推理，由平面展开图还原为正方体，根据正方体性质判断。

第十二题：

必备知识：本题主要考查的知识是“判断函数奇偶性”，“正余弦二倍角公式”，“辅助角公式”，“根据三角函数性质求函数最值”，“导函数求单调性”。

学科素养：本题考查的学科素养是数学运算，逻辑推理，数学建模，数据分析。三角函数有关的复杂函数的研究，一般先研究其奇偶性和周期性，而单调性的研究需看函数解析式的形式，比如正弦型函数或余弦型函数可利用整体法来研究，而分式形式则可利用导数来研究，注意辅助角公式在求最值中的应用．

第十三题：

必备知识：本题主要考查的知识是“圆台的体积”和“外接球问题”，了解圆台的体积公式。

学科素养：本题考查的学科素养是直观想象和数学运算。圆台与球的切接问题，解题的关键在于确定下底面与球的关系，然后利用几何关系确定圆台的高度即可求得其体积.

第十四题：

必备知识：本题主要考查的知识是“直线斜率的概念”和“正切和差公式”，会用正切的和差公式，了解直线概率的概念。

学科素养：本题考查的学科素养是数学运算，直观想象和逻辑推理。先设对角线的倾斜角

，利用斜率定义列关系

，结合正方形性质求得直线

与直线

的倾斜角，计算正切值即可。

第十五题：

必备知识：本题属于开放题，答案没有限制，满足条件即可，考查的知识是“函数的奇偶性”，理解函数奇偶性的概念即可。

学科素养：本题考查的学科素养是逻辑推理，根据奇函数性质可考虑函数类型求解。

第十六题：

必备知识：本题主要考查的知识是“正态分布”了解正态分布曲线的对称性。

学科素养：本题考查的学科素养是数学运算，数据分析。对正态分布的考查，关键点在于能从

读出所需信息。

第十七题：

必备知识：本题主要考查的知识是“等比数列的定义”，“构造数列”，掌握等比数列的概念，会用待定系数法进行求解。

学科素养：本题考查的学科素养是数学运算和数据分析。通过对数据的分析，运用待定系数的方法求解。

第十八题：

必备知识：本题主要考查的知识是“余弦定理”，掌握余弦定理的应用。

学科素养：本题考查的学科素养是逻辑推理，数学运算，直观想象。通过命题创新，考查考生能够将已知条件与正弦定理和余弦定理联系起来，通过对条件和结论的分析，理解正、余弦定理运算法则，合理选择运算方法，解决问题。

第十九题：

必备知识：本题主要考查的知识是“相互独立事件”，“离散型随机变量的分布列与期望”，掌握相互独立事件，利用对立事件概率公式求解。能够根据离散型随机变量的概念求的分布列和期望。

学科素养：本题考查的学科素养是数据分析和数学运算。求离散型随机变量X的数学期望的一般步骤：

（1）先分析X的可取值，根据可取值求解出对应的概率；

（2）根据（1）中概率值，得到X的分布列；

（3）结合（2）中分布列，根据期望的计算公式求解出X的数学期望.

第二十题：

必备知识：本题是一道新定义的创新题，结合生活实际进行考查，试题主要考查的知识是“理解定义的能力”，“运用定义的能力”，“空间想象能力”

学科素养：本题考查的学科素养是逻辑推理和空间想象。试题考查立体几何的新定义问题，能够正确读懂“曲率”的概率是解决问题的关键．

第二十一题：

必备知识：本题主要考查的知识是“双曲线的离心率”，“双曲线的渐近线”，“直线的斜率”和“二倍角的正切值”。

学科素养：本题考查的学科素养是逻辑推理，数学运算，数据分析。圆锥曲线中离心率的计算，关键是找到

一组等量关系。圆锥曲线中与有角有关的计算，注意通过动点的坐标来刻画角的大小，还要注意结合点在曲线上满足的方程化简目标代数式。

第二十二题：

必备知识：本题主要考查的知识是“构造新函数”，“利用导数研究函数的单调性”，能够通过分离参数得出所要构造的函数，在利用函数的单调性求得最值解题。

学科素养：题考查的学科素养是“逻辑推理”，“数学运算”，“数据分析”。通常要构造新函数，利用导数研究函数的单调性，求出最值，从而求出参数的取值范围；利用可分离变量，构造新函数，直接把问题转化为函数的最值问题；根据恒成求解参数的取值时，一般涉及分离参数法，但压轴试题中很少碰到分离参数后构造的新函数能直接求岀最值点的情况，通常要设出导数的零点，难度较大.

,