古埃及数学包括哪些内容（公元前1550的莱茵德数学纸草）

背景

莱因德数学纸草是古埃及数学中最著名的例子之一。它是以苏格兰古物学家亚历山大·亨利·莱因德的名字命名的，他于1858年在埃及卢克索购买了这张纸草；它是在底比斯拉姆塞姆或附近的非法挖掘中发现的，可以追溯到公元前1550年左右。莱因德纸草比莫斯科数学纸草大，而后者更古老。莱因德纸草现藏于大英博物馆，编号10057和10058。第一部分（BM 10057）：长度： 295.5厘米，宽度：32厘米；第二部分（BM 10058）：长度： 199.5厘米，宽度：32厘米。纽约市的布鲁克林博物馆收藏了一个18厘米小碎片，刚好是10057和10058的链接部分。

莱因德数学纸草可以追溯到埃及的第二个中间期。它被抄写员Ahmes复制（即Ahmose；阿姆斯是数学历史学家最喜欢的更古老的抄写），来自国王阿蒙尼姆哈特（Amenemhat III）三世（第12王朝）统治时期的文本。这份埃及手稿用僧侣体文字书写，高33厘米（13英寸），由多个部分组成，总共超过5米长。纸草在19世纪末开始被翻译。数学翻译方面在几个方面仍然不完整。这份文件的日期是希克索斯国王阿波菲斯（Apophis）的33年；另外，在其反面还包含了一个单独的历史注释，可能可以追溯到他的继任者哈穆迪（Khamudi）的时期（“11年”）。

一些关于莱因德数学纸草的书籍和文章已经出版，其中有一些脱颖而出。《莱因德纸草》由皮特于1923年出版，包含了对格里菲斯的书I、II和III大纲的文本讨论。Chace在1927-29年出版了一本概要，其中包括文本的照片。罗宾斯和舒特在1987年发表了关于莱因德纸草的最近的概述。

莱茵德纸草外观及布局

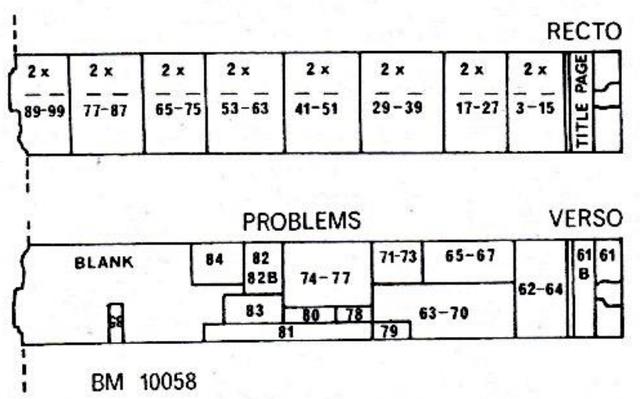
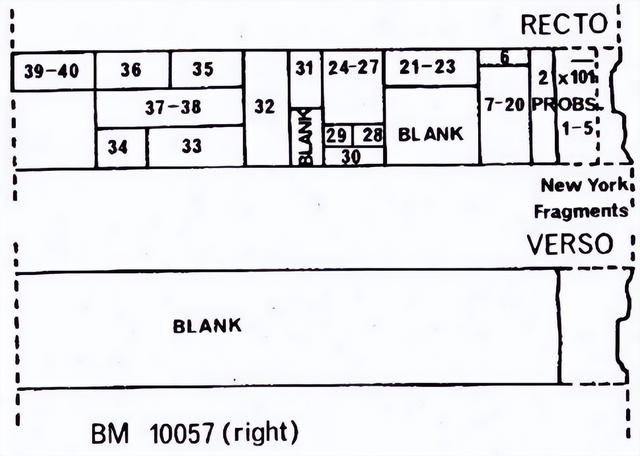
目录

Table of 2/3

Book I. Arithmetic.算术

Nos. 1-6. Division of various numbers of loaves equally between 10 men.

Nos. 7-20. First group of completion-calculations (seken) involving multiplication of fractions.

Nos. 21-23. Second group of completion-calculations, involving simple addition of fractions.

Nos. 24-34. Arithmetical solution by trial of equations of the first degree.

Nos. 35-38. Similar equations involving the bushel or hekat.

Nos. 39 and 40. Division of loaves between men in unequal proportions.

Book II. Mensuration.测量

Part I. Volumes and cubic content in corn.

Nos. 41-43. Cylindrical containers.

Nos. 44-46. Rectangular parallelopipedal containers.

No. 47. Expression incorrect form of 1/10, 1/20, up to 1/100 of a hekat, disguised as a sum in cubic

content.

Part II. Areas.面积

No. 48. Area of a square and circle compared.

No. 49. Rectangle

No. 50. Circle.

No. 51. Triangle.

No. 52. Truncated triangle.

No. 53. Trapezoid (?).

Nos. 54 and 55. Division of given area of land into equal-sized fields

Part III. Batter, or angle of slope. 陡度

Nos. 56-59. Batter of pyramid.

No. 60. Slope of a cone (?).

Book III. Miscellaneous problems in arithmetic. 杂项

No. 61. Multiplication of fractions (probably out of place, see above).

No. 62. Proportionate values of precious metals.

No. 63. Division of loaves in unequal proportions.

No. 64. Division of barley into shares in arithmetical progression.

No. 65. Division of loaves in unequal proportions.

No. 66. Daily portion of a yearly ration of fat.

No. 67. Reckoning of livestock.

No. 68. Division of 100 hekat of corn in unequal proportions.

Nos. 69-78. So-called pefsu-reckonings. Conversion of grain into bread and beer, and the barter of

these last.

No. 79. Geometrical progression.

No. 80-1. Conversion of fractions of the hekat (1/2, 1/4, 1/8, etc.) into henu.

No. 82-3. Food estimate for a poultry yard.

No. 84. Estimate of food of an ox-stall.

Additions.

No. 85. Unintelligible group of signs.

No. 86. Fragment of accounts.

No. 87. Calendrical entries.

从目录、前言和内容的编排来看，莱茵德纸草比卡宏纸草和莫斯科纸草更为成熟、是由目的、有层次的编排，故以下按照序号整理，保持原稿思想的完整性。因为计算的方式与现代差别很大，可借鉴的意义不太，因此，计算部分从简从略。“Note”为译者、整理者关于此项的简单批注，以辅助了解原稿之思想大意，不是原作者的表达。

序言

在纸草的开头段落中，作者Ahmes说：

“对所有现有的事物和所有模糊的秘密的知识进行准确的计算。这本书是在第33年，在洪水季的第4个月，在上埃及和下埃及国王A-user-Re的威严下，赋予生命，仿照上埃及和下埃及国王Ne-ma'et-Re时代的古代著作，书记员Ahmes抄写了这篇文章。”

Note：从扉页上可以清楚地看出，Ahmes介绍了他自己和写作的历史背景与目的，既确定了成书年代，也确定了一个更古老的文本或他所复制的文本的时期。

2/n表

Note：2/n表是将从2/n（n=3~101的奇数）表示为埃及分数，既单位分数（1/m,m为自然数）之和。在整个纸草中，大多数解都是用特定埃及分数表示。除了整数和2/3之外，Ahmes均是使用（正的）单位分数来表达埃及分数。然而，由于每一个正有理数都可以用无限多个单位分数来表示，这些解不是唯一的。人们通常好奇埃及人如何求得这些单位分数，RMP问题61B提示将2/n表示为2项的埃及分数方法。然而，当n是素数时，在许多情况下，这个羽翼未丰的算法就被抛弃了。因此，2/n表的解方法也暗示了数论的开端，而不仅仅是算术。

2/3  = 1/2 1/6

2/5   = 1/3 1/15

2/7  = 1/4 1/28

2/9  = 1/6 1/18

2/11  = 1/6 1/66

2/13 = 1/8 1/52 1/104

2/15 = 1/10 1/30

2/17  = 1/12 1/51 1/68

2/19 = 1/12 1/76 1/114

2/21 = 1/14 1/42

2/23  = 1/12 1/276

2/25 = 1/15 1/75

2/27 = 1/18 1/54

2/29  = 1/24 1/58 1/174 1/232

2/31 = 1/20 1/124 1/155

2/33 = 1/22 1/66

2/35  = 1/30 1/42

2/37 = 1/24 1/111 1/296

2/39 = 1/26 1/78

2/41  = 1/24 1/246 1/328

2/43 = 1/42 1/86 1/129 1/301

2/45 = 1/30 1/90

2/47  = 1/30 1/141 1/470

2/49 = 1/28 1/196

2/51 = 1/34 1/102

2/53  = 1/30 1/318 1/795

2/55 = 1/30 1/330

2/57 = 1/38 1/114

2/59  = 1/36 1/236 1/531

2/61 = 1/40 1/244 1/488 1/610

2/63 = 1/42 1/126

2/65  = 1/39 1/195

2/67 = 1/40 1/335 1/536

2/69 = 1/46 1/138

2/71  = 1/40 1/568 1/710

2/73 = 1/60 1/219 1/292 1/365

2/75 = 1/50 1/150

2/77  = 1/44 1/308

2/79 = 1/60 1/237 1/316 1/790

2/81 = 1/54 1/162

2/83  = 1/60 1/332 1/415 1/498

2/85 = 1/51 1/255

2/87 = 1/58 1/174

2/89  = 1/60 1/356 1/534 1/890

2/91 = 1/70 1/130

2/93 = 1/62 1/186

2/95  = 1/60 1/380 1/570

2/97 = 1/56 1/679 1/776

2/99 = 1/66 1/198

2/101 = 1/101 1/202 1/303 1/606

1-9/10 T表

Note：1-9/10表是将1/10~9/10表示为埃及分数

1/10=1/10

2/10=1/5

3/10=1/5 1/10

4/10=1/3 1/15

5/10=1/2

6/10=1/2 1/10

7/10=2/3 1/30

8/10=2/3 1/10 1/30

9/10=2/3 1/5 1/30

Problems 1–6：1、2、6、7、8和9条面包（在每个问题中分别）被分成10个人，每个人所得到的面包数是多少？

Note：对1-9/10表的上手练习。

7,7B, 8–20：求不同的埃及分数与S或T相乘的数值，用埃及分数表示。S=1 1/2 1/4, T=1 2/3 1/3。

Note：埃及分数的乘法

21–38：求解带有一个变量的线性方程，并表示为一个埃及分数。

Note：尽管对问题21-38的陈述有时看起来很复杂，例如问题31有一个特别繁重的解决方案，但每个问题最终都被简化为一个简单的线性方程。用分数而不是小数来表示一个数值的方法似乎不会引入因“近似”带来的相对错误或误差。

39：100条面包将被不平等地分配给10人。50块面包将平均分给4人，这样4人每人得到平等的份额，而其他50块面包将平均分给其他6人，这样6人每人得到平等的份额。找出这两种分配的差异，表达与埃及分数。

Note：在问题39中，纸草开始考虑有多个变量的情况。

40：100块面包将分给五个人。五个人得到的面数量是一个连续的等差数列。此外，三个最大的份额的总和等于两个最小的份额的总和的7倍。每个人得到面包的差额是多少？ 问题40在今天看起来是一个2元一次方程。

Note：问题40是纸草的算术/代数部分的最后一题，后面是几何部分。在问题40之后，纸草上甚至有很大的空白空间，它直观上表示该部分的结束。

41：计算直径为9cubit、高度为10cubit的圆柱形粮仓的体积。用cubit cubit单位给出答案，并换算为其他体积单位：1cubit cubit= 3/2khar= 30heqats= 15/2quadruple heqats。

Note：这个问题打开了纸草的几何部分，也给出了第一个事实不正确的结果（使用8/9作为内接圆的边长来计算其面积，尽管有一个很好的近似）。

42：重用41中给出的体积公式和单位信息，计算出直径为10cubit、高度为10cubit的圆柱形粮仓的体积。

Note：问题42实际上是41的重复，在最后执行类似的单位转换。

43：计算体积的圆筒形颗粒筒仓的直径9cubit和6cubit的高度，数值用khar的埃及分数表示 。

Note：问题43代表了纸草上第一个严重的数学错误。Ahmes（或他复制的来源）尝试了一种捷径，希望体积计算从cubit到khar实现单一步骤单位转换，以避免在初始结果中使用cubit。然而，这种尝试失败，原因是混淆了在41和42过程的一部分，可能是为了用于43，通过不同的方法提供一致的结果，结果却导致一个新的、与近似用于41和42体积公式不一致的结论。

44, 45：一个cubit cubit等于15/2 quadruple heqats。（44）一个边长度为10 cubit的立方形粮仓，。用quadruple heqats来表示其体积。另一方面，（45）考虑一个体积为7500 quadruple heqats的立方形粮仓，并用cubit表示其边长。

Note：问题45是问题44的逆计算，因此它们在这里一起呈现。

46：一个矩形棱柱形粮仓的体积为2500 quadruple heqats量。用cubit来描述它的边长。

Note：如上所述，这个问题有无穷多个解，但这里给出了与44和45项密切相关的简单解的情况。

47：将100 quadruple heqats的体积量除以10的倍数，从10到100。用quadruple heqat、quadruple ro表示结果。

Note：在第47题中，Ahmes特别坚持尽可能地将更复杂的分数串表示为荷鲁斯眼分数。比较问题64和问题80的相似的表示偏好。

48：比较一个直径为9的圆和一个边长为9的正方形。圆的面积和正方形的面积的比例是多少？

Note：48-55处理正方形（近似圆）、直角三角形、直角梯形的平面的面积计算。

问题48的陈述和解决方案明确说明了近似圆面积的首选方法，其结论为64/81,这在问题41-43中已经使用过。然而，这是近似的。问题48的最初陈述涉及使用一个称为setat的面积单位，将在此后的问题中提供进一步的背景。目前，这只是一种伏笔。

49：长度的单位1khet=100cubit。此外，“cubit strip”是用于测量面积的矩尺，由1cubit乘100cubit，或100平方cubit（或等面积的物理量）。考虑一个10khet的矩形土地。用cubit strip来表示其面积。

50：考虑一个直径为9 khet的圆。用setat来表示其面积。

Note：问题50是有效地强化了48的64/81规则的圆形面积，A=64setat作为一个普适常数。

51：一块三角形的土地的底部为4khet，高度为10khet。用setat来表示这个面积。

Note：51的题设和解决方案似乎表达了我们熟悉的计算直角三角形面积的公式。

52：一块梯形的土地有两个基部（底边、顶边），分别为6khet和4khet。它的高度是20khet。用setat来表示这个面积。Note：52的题设和解决方案似乎表达了我们熟悉的计算直角梯形面积的公式。

53：一个等腰三角形（比如说，一块陆地）有一个底边等于4 1/2 khet，一个高度等于14 khet。平行于底边的两个线段进一步将三角形划分为三个扇区，即一个底部的梯形、一个中间的梯形和一个顶部（类似的）较小的三角形。线段在三角形的中点(7)，在靠近底部的四分之一点（3 1/2）进一步切割，因此每个梯形的高度为3 1/2 khet，而较小的类似三角形的高度为7 khet。求出两个线段的长度，其中它们分别是短线段和长线段，并用埃及的khet的分数项表示。此外，找出三个扇区的面积，其中它们分别是大梯形、中间梯形和小三角形，并用埃及setat和cubit strip的分数项表示。使用1setat= 100cubit strip进行单位转换。

Note：53题似乎非常能够说明他们在洪水过后的土地测量和分配时的实用性。

54：这里有10块土地。在每个地块中，一个扇区被分割出来，这样这10个新分区的面积之和为7setat。每个新的分区都有相等的面积。求出这10个新分区中的任何一个的面积，用埃及的setat和cubit strip来表示。

Note：54题似乎非常能够说明他们在土地测量和重新分配时的实用性。

55：这里有5块土地。在每个地块中，一个扇区被分割出来，这样这5个新分区的面积之和为3setat。每个新的分区都有相等的面积。求出这5个新分区中任何一个的面积，用埃及的setat和cubit strip来表示。

56：1）1royal cubit（皇家肘尺）=7palms（掌），1palm=4finger（指）。换句话说，以下等式保持：1（royal）cubit=1cubit=7palms= 28fingers。

2)考虑一个正方形金字塔，其底部，方形面与一个平面（或地面）共面，因此任何包含其三角形面的平面相对于地面平面（即金字塔的内部）具有二面角θ。换句话说，θ是金字塔的三角形面相对于地面的角度。对于这样一个金字塔，高度a和底边b，陡度Seked定义为：S/1royal cubit =cotθ。换句话说，金字塔可以解释为它的三角形面逐渐上升的比率。或者，在金字塔内部，满足这样一个直角三角形，直角边为a，b/2,斜边是三角形面的垂直平分线，金字塔满足

Cotθ=b/2a=S/1royal cubit, 因此，我们描述了类似的三角形，其中一个可以缩放为另一个。

1. 金字塔的高度是250royal cubit，它的底部有360 royal cubit。求这样一个金字塔的Seked，用royal cubit 和palm表示。

Note：问题56是莱因德纸草上的第一个“金字塔问题”或seked问题，56-59,59B和60都是涉及金字塔相对于平面的面部倾斜角/陡度的概念。在这方面，seked的概念暗示了三角学的早期开始。然而，与现代三角学不同的是，特别注意的是关于某些金字塔的seked，它本身是一种物理长度测量，可以以任何物理长度单位给出。

57, 58：（57）金字塔的陡度是5plam1finger，它的底边是140cubit。求它的高度。（58）一个金字塔的高度是93 1/3cubit，其底部的侧面是140cubit。求它的陡度seked，用palm和finger来表示。

Note：问题58是问题57的逆运算，因此它们在这里一起呈现。

59, 59B：（59）一个金字塔的高度是8cubit，它的基底边长度是12cubit。求它的陡度seked，用palm和finger来表示。（59B），一个金字塔的底边是5palm1finger，它的底边是12cubit。求它的高度，用cubit来表示。

Note：问题59和59B考虑一个类似于57和58的案例，以熟悉的结果结束。作为彼此之间的逆运算，它们在这里一起呈现。

60：如果一个“柱子”（即圆锥体）的高度为30cubit，而它的底部（或直径）的长度为15cubit，求它的陡度seked，并用cubit来表示。

Note：Ahmes使用稍微不同的词来呈现这个问题，这有助于翻译问题。问题60总结了纸草的几何部分。此外，这是文件的正面（recto）的最后一个问题；本摘要后面的所有内容都出现在莎草纸的背面（verso）。因此，从60到61的过渡是纸草的主题和物理转变。

61：17个乘法将使它们的产物用埃及分数表示。整个部分将作为一个表来给予。

Note：原始文档的语法及其重复的乘法表明了对乘法是可交换的基本理解。

61B：给出一个一般的程序，将2/3的随机（正的）奇数2n 1的乘积转换为两项埃及分数的和，

Note：问题61B，以及它所描述（和建议）的分解方法与莱因德数学纸草2/n表的计算密切相关。特别地，在2/n表中涉及一个分母为3的倍数的每个情况都可以说遵循61B的例子。61B的陈述和解决方案也暗示了一种纸草中大多数其他的更具体的问题，所没有的普遍性。因此，它代表了代数和算法的早期建议。

62：一个袋子里有三种贵金属，黄金，白银和黑铅，花了84shaty，这是一个货币单位。这三种物质的重量都一样的，1deben是重量单位。1deben黄金价格是12sahty，1deben的白银价格是6shaty，1deben黑铅的价格是3sahty。求袋子里这三种金属的重量。

Note：问题62是一个日常可能发生的经济问题。

63：700个面包不平均地分成四个人，分配将按相应的比例

。求出每个人分配的份额。

64：heqat是一个体积单位。10hepat大麦将以算术顺序分配给10个人，因此连续份额的差异为1/8。找到这十个份额，并按降序排列，用hepat的埃及分数。

Note：问题64是40的变体，这次涉及到偶数个的未知数。除了埃及分数之外，份额的范围从25/16下降到7/16，其中分子以连续的奇数下降。这是是荷鲁斯眼分数；比较47和80个问题。

65：100块面包要不平均地分给10个人。其中七个人得到一份，而另外三个人，分别是船夫、工头和看门员，每人得到两份。将这两种份额表示为埃及分数。

66：体积换算1hepat=320 ro。在一年（365天）的时间里，分配给1人每天等量的脂肪。用heqat和ro的埃及分数表示。Note：问题66在其原始形式中明确规定，一年等于365天，并反复使用数字365进行计算。因此，它是古埃及人理解这个年份的主要历史证据。

67：一个牧羊人有一群动物，他必须把他的羊群的一部分送给一个领主进贡。牧羊人被告知给予他原来羊群三分之一的三分之二作为贡品。牧羊人给了70只动物。求牧羊人原来的羊群的大小。

Note：实际可能会用到经济问题

68：四名监督员负责四个团队，团队成员分别为12人、8人、6人和4人。每个成员的工作速度可替代，生产一种单一的产品：生产（比如采摘）谷物。在一段时间内，这四个团队总共生产100 quadruple heqats 的谷物，每个成员的产品将交给这个团队的监督员。用quadruple heqat来表示每个团队的产量。

69：1）考虑烹饪和食物准备。假设有一种标准化的烹饪方法，或一种生产过程，食品原料和某种成品采取体积单位hepat来表示。那么，一份成品相对于一份原料的pefsu定义为从一体积hepat或一份原料中产生的一个体积hepat或一份成品的数量。

1. 3 1/2hepat的面粉产出80块面包。求出每个面包消耗的面粉数量pefsu，用hepat的埃及分数来表示。

Note：问题69开始了“pefsu”问题，69-78，在食物准备的背景下。pefsu的概念假设了一些标准化的生产过程，没有意外、浪费等，并且只涉及一种标准化的成品与一种特定原材料的关系。也就是说，暂不涉及生产时间，或（在任何一种情况下）其他原材料或设备与生产过程的关系等问题（单变量研究）。尽管如此，pefsu的概念是纸草中的另一个抽象的暗示，能够应用于食品（或成品）和原材料之间的任何二元关系。因此，制造业所包含的概念是典型的制造业。

70：（7 1/2 1/4 1/8）hepat的面粉可以产生100个面包。求出每个面包消耗的面粉数量pefsu，用hepat的埃及分数来表示。

Note：同69，不同类型的面包

71：1/2hepat的原料besha生产1des-measure啤酒。假设有一个啤酒的生产过程，将用到被稀释的啤酒。刚才描述的啤酒的1/4被倒出来，刚刚倒出来的啤酒被重复使用。这种啤酒，现在只有3/4，然后用水稀释到满刻度，正好产生一杯完全稀释的啤酒。求这些稀释啤酒的pefsu，用hepat的埃及分数来表示。

Note：请注意，问题71描述了生产过程中的中间步骤，以及第二种原料，即水。进一步注意，这些与成品单元和原材料之间的关系（在本例中是besha的）无关。

72：100个“pefsu10”的面包将被平均地交换为“pefsu45”的面包。求这个数。

Note：既然pefsu的概念已经建立，问题72-78甚至探索替换不同的成品，有不同的pefsu。然而，一般来说，它们采用了某种共同的原材料。具体来说，在72-78年啤酒中，常见的原料被称为wedyet面粉，它甚至与啤酒的生产有关，因此在后一个问题中，啤酒可以换成面包。74的原始声明也提到了“上埃及大麦”，但为了我们的目的，这是化妆品。72-78提出的问题实际上是：在两个不同的生产过程中使用等量的原材料，生产两种不同单位的成品食品，每种类型都有不同的pefsu。找到另一个。这可以通过将两个单位（已知的和未知的）除以它们各自的pefsu来实现，其中成品食品的单位在维度分析中消失，并且只考虑相同的原材料。然后可以很容易地解x。72-78因此，确实需要给出x，以便在两个不同的生产过程中使用等量的原材料。

73：100个pefsu 10面包均匀交换pefsu 15面包。求出这个数。 -

74：1000个含有pefsu 5的面包将被平均分成两堆，每堆500个面包。每堆要均匀地交换另外两个堆，一个pefsu 10，另一个pefsu 20。求出这个两个数。 -

75：155个pefsu 20面包均匀交换pefsu 30面包。求出这个数。 -

76：1000块10堆pefsu 10的面包，将被均匀地交换成另外两堆面包。另外两个面包堆各有相同数量的面包，一个是pefsu 20，另一个是pefsu 30。求出这个数。 -

77：10 des-measure的啤酒，pefsu 2，均匀地换成面包，pefsu 5。求出这个数。 -

78：100块面包，pefsu 10，将被平均地交换成pefsu 2的啤酒。求这个数。 -

79：一个庄园有7所房子，49只猫，343只老鼠，2401株斯佩尔特小麦和16807hepat麦粒。作为一个表格列出，并包括它们的总数。

Note：问题79已经得到了最字面化的解释。然而，这个问题是最有趣的纸草，其设置甚至解决方法表明几何级数的基本理解。在原始文件中，2401术语被写成2301（一个明显的错误），而其他术语的给出是正确的；因此在这里进行了修正。

80：Hinu是体积的单位，10hinus=1hepat。考虑有一个荷鲁斯眼分数的情况，并在表中换算为hinu。

Note：比较问题47和64的其他表格信息，重复的荷鲁斯眼分数。

81：“hinu的单位转换”。也就是说，表达了埃及分数的分类，其中许多术语也是荷鲁斯眼分数，在各种术语中，heqat、hinu和ro。

Note：问题81的主要部分是一个更大的埃及分数分类转换表，它扩展了问题80的概念——事实上，它代表了整个纸草中最大的表格形式之一。问题81的第一部分是问题80中的表的精确重复，其中第一行1 heqat = 10 hinu缺损；因此，这里不重复。问题81的第二部分，或它的“主体”，是这里给出的大表。细心的读者会注意到两件事：几行重复相同的信息，在表两边的“heqat”区域给出的几个形式（但不是全部）实际上是相同的。有两点值得一提，这可以解释为什么这个表格看起来是这样的。首先，Ahmes实际上在表的不同区域完全重复了某些信息组，因此在这里重复。另一方面，Ahmes也以某些“左手”geqat公式形式开始，并在他早期的计算中犯了一些错误。

然而，在许多情况下，他在后来写的表格中纠正了这些错误，产生了一致的结果。因为目前的信息只是重建Chace的翻译和解释的纸草，因为Chace选择解释和纠正Ahmes的错误，用后来正确的信息在某些早期行，从而修复错误，因此重复信息在翻译过程中，这种解释方法解释了某些信息的重复行。至于某些列中的信息重复情况（1/4heqat=……=1/4heqat等），这似乎只是一个惯例，Ahmes在考虑某些重要的荷鲁斯-眼分数比时，既从Chace的角度，也从heqat（和他们的交互）。简而言之，信息的各种重复是Ahmes、他的潜在源文件和Chace的编辑选择的结果，目的是对问题81中的大表进行数学上一致的翻译。

82：假设 wedyet面粉制成面包，作为每天十只育肥鹅的饲料。为此，请执行以下计算，用埃及分数表示hundreds of heqats, heqats，ro数量，另有规定的除外：

以“10只肥鹅一天吃2 1/2heqat”的声明开始。换句话说，每日的消耗率（和初始条件）等于2 1/2。测定10只育肥鹅在10天和40天内吃的heqat数。将这两个数分别称为t和f。

将上述后一个数量f乘以5/3来表示需要收获的“二粒小麦”的数量s；

f乘以2/3来表示所需要的普通“小麦”的数量w。

w除以10表示需要减去的“小麦”数量。

求：f-p=g。“谷物”（wedyet面粉）的数量，这是喂养鹅所必需的，假设间隔40天（这似乎在一定程度上与问题的最初说法相矛盾）。最后，再次使用以下单位表达g数量hundreds of double heqats, double heqats 及double ro, 其中 1 100 double heqat = 2 hundred heqat = 100 double heqat = 200 heqat = 32,000 double ro = 64,000 ro.这个数称为g2.

Note：从问题82开始，纸草变得越来越难以解释（由于错误和信息缺失），直到难以理解的程度。然而，82还有可能有一些意义。简单地说，对于在烹饪或生产过程中提取的食品材料的分数，似乎存在着既定的规则，或良好的预算。Ahmes的82只是简单地表达了其中一些数量的表达，毕竟在原始文件中宣布是一个“估计”，尽管它的语言有些矛盾和混乱。

奇怪的是，问题82、82B、83和84也以延续最近的宠物问题的“食物”思路而闻名，这次考虑的是如何喂养动物而不是人。82和82B都使用了关于t和f的“百heqat”单位；这些约定是修饰性的，在这里不再重复。在这些最后的问题中（每个Chace）也会采取许可来修复原始文件的数字错误，以试图呈现一个连贯的释义。

82B：估计出其他鹅的饲料量。也就是说，考虑一个与问题82相同的情况，只有一个例外，即初始条件或每日消耗率正好是问题的一半。也就是说，让i= 1 1/4。求出t、f、g2数量，特别是通过使用初等代数来跳过中间步骤。

Note：问题82B与问题82并行提出，并快速考虑了相关量减半的相同情况。在这两种情况下，Ahmes的真正目标似乎都是找到g2。现在他有了一个“程序”，他觉得可以自由地跳过82号的繁重步骤。我们可以简单地观察到，2的除法完成了整个问题的工作，因此g2也正好是问题82的一半大。使用初等代数的一个稍微彻底的方法是回溯82中的量之间的关系，观察g = 14/15 x f，然后执行单位转换将g转换为g2。

83：估计各种鸟类的饲料。这是一个具有多个组件的“问题”，可以解释为一系列的评论：

假设四只鹅被关起来，它们每天的饲料量等于1hinu。用heqat和ro表示一只鹅每天消耗的饲料。

假设“进入池塘”的鹅的每日饲料等于1/16 1/32heqat 2 ro。用hinu表示一只鹅每天消耗的饲料。

假设10只鹅的饲料量为1heqat。求出这些动物10天、和30天或一个月消耗的饲料数量。

最后，提供一张表格，提供每日饲料，使任何指定物种的动物肥胖。

Note：由于问题83的各种项目都是关于heqat、ro和hinu之间的单位转换，按照80和81的精神，我们很自然地想知道表格上的项目在转换为hinu时会变成什么。鹅、尾鹅和鹤的份额为5/3，野鸭的比例为1/2，尾鹅的比例为1/4（比较问题的第一项），鸽子和鹌鹑的份额为1/16 1/32。荷鲁斯眼分数的存在与纸草的其他部分很熟悉，表格似乎考虑了鸟类的饲料估计，从最大到最小不等。在表的顶部的“5/3hinu”部分，特别是它的5/3的因子，提醒了在问题82中找到s的方法之一。问题83提到了“下埃及谷物”，或大麦，它也在一个地方使用了“hundred-heqat”单位；这些是伏笔，没有在目前的声明中。

84：估计马厩牛的饲料。

Note：84是最后一个问题，或数字，包括莱因德纸草的数学内容。关于84本身，查斯呼应了皮特：“人们只能同意皮特的观点，‘对于这个问题，纸草达到了不可理解和不准确的极限。‘“（Chace，第2节，问题第84期）。在这里，“百个heqat”单元的实例已经用“c.heqat”来表示，以节省空间。上面提到的三头“牛”被描述为“普通”牛，以区别于其他动物，而关于面包和“普通食物”的两个头是关于热量的。桌子开始的“好牛”被描述为上埃及牛，这个短语也在这里因为空间的原因被删除了。

问题84似乎提出了一种程序，以与前三个问题相似的术语来估计各种食品材料和津贴，但现有的信息却非常混乱。尽管如此，还是有一些一致性的迹象。这个问题一开始就像一个传统的故事问题，描述一个有四种不同类型动物的马厩。似乎这四种类型的动物以不同的速度消耗饲料，或“面包”，并且有相应数量的“普通”食物。这两列信息被正确地总结在“总”行中，但是它们后面是两个与上面的关系可疑的“二粒小麦”项。这两个拼写项确实分别乘以10，从而得到“10天”行中的两个条目。

85：一小群草书象形文字，查斯认为这可能代表抄写员“尝试他的笔”。它似乎是某种短语或句子，并建议进行两种翻译。1)“杀死害虫、老鼠、新鲜的杂草和大量的蜘蛛。”祈求上帝得到温暖、风和充分的水。”2)解释这个抄写员写的奇怪的事情……根据他所知道的。”

Note：其余的第85、86和87项是各种非数学性质的勘误表，因此Chace将其命名为“数字”，而不是问题。它们也位于纸草的区域，远离文字的主体，这刚刚以问题84结束。例如，85号离问题84有一定距离，但不是太远。因此，它在纸草上的位置暗示了一种结尾，在这种情况下，后一种翻译，Chace描述为古埃及文件的“神秘的写作”解释的一个例子，似乎最适合它在文件中的上下文。

86：第86号似乎来自某个帐户，或备忘录，并列出了各种各样的商品和数量，使用的词语与纸草本身的其余部分相熟悉的语境。[原文是一系列的文字，因此编号如下。]

1...永远活下去。Hebenti的食物清单。

2... 他的兄弟是管家Ka-mose。

3... 在他的一年中，一年两次50件白银。

4... 牛2，银3块。

5... 一个两次；也就是说，1/6和1/6。现在是一个。。

6...12 hinu；也就是银，1/4；一个..。

7... (金或银)5块，价格, 因此；鱼，120，两次。

8... 年，大麦，100 1/4 quadruple heqat；二粒小麦100heqat... heqat...。

9... 大麦，quadruple heqat，100 heqat 15 heqat的1/2 1/4；二粒小麦1 1/2 1/4倍 100 heqat 17 heqat。

10...146 1/2；大麦， 100 heqat 10 heqat; spelt, 300 heqat... heqat...

11...1/2，带来了酒，一驴（装载？）。

12... 银1/2件；也就是说，银的。

13...1 1/4；脂肪，36 hinu；也就是说，是银色的。

14...1 1/2 1/4倍 100 heqat 21 heqat；二粒小麦，400 heqat 10 heqat...

第15-18行（这些行是第14行的重复。）”

Note：Chace指出，86被粘贴在垂直面的最左边（与后来的几何问题相反），以加强纸草。因此，第86号可以被解释为一张“废纸”。

87：第87号报告是对某些事件的简要描述。Chace指出了一个（公认的日期和可能改变了）学术共识，即87在纸草完成数学内容后不久就被添加到纸草上。他接着指出，其中所描述的事件“发生在Hyksos统治时期”。

“第11年，收获季节的第二个月。已输入螺旋流。

淹没季节的第一个月，第23天，军队的指挥官（？）攻击Zaru.

第25天，听说扎鲁进去了。

第11年，淹没季节的第一个月，第三天。Set出生；这个神的威严使他的声音被听到。

Isis诞生了，天上就下雨了。”

Note：87号位于垂直层的中间，被一个大的，空白的，未使用的空间所包围。

参考资料

https://wiki.alquds.edu/?query=Rhind_Mathematical_Papyrus

,